De cirkel van Apollonius is de meetkundige plaats is van de punten waarvan de afstand tot twee vaste punten gelijk is aan a : b.
We bekijken nu de verzameling van de punten waarvoor de afstanden tot twee vaste rechte lijnen gelijk is aan a : b.
Isogonale verwantschap, antiparallel, punt van Lemoine
Zie ook het Cabri-werkblad
"Isognaalafbeelding".
Zie ook de pagina "Meer over isogonale verwantschap" /
Zie ook de pagina "Twee raaklijnen aan een ellips"
1. Inleiding, isogonale verwantschap ![]()
De cirkel van Apollonius is de meetkundige plaats is van de
punten waarvan de afstand tot twee vaste punten gelijk is aan a : b.
We bekijken nu de verzameling van de punten waarvoor de afstanden tot twee vaste rechte
lijnen gelijk is aan a : b.
| Stelling 1 De meetkundige plaats van de punten waarvan de afstand tot twee snijdende lijnen l en m zich verhouden als twee lijnstukken a en b, bestaat uit twee rechten door het snijpunt van l en m. |
Bewijs: Zie figuur 1.
| figuur 1 | 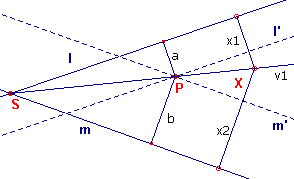 |
Het punt P, waarvan de afstand tot l gelijk is aan a en
de sftand tot gelijk is aan b behoort in ieder geval tot de verzameling (P
is het snijpunt van de lijnen l' en m' op afstand a resp. b
van l en m). Zij X een punt op de halve lijn v1 door S en P. Nu is SP : SX = a : x1 SP : SX = b : x2 Zodat a : x1 = b : x2 of x1 : x2 = a : b De lijn v1 behoort dus tot de verzameling. |
Omgekeerd.
| figuur 2 | 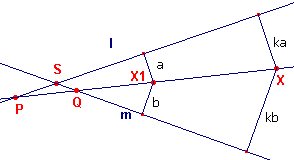 |
Stel het punt X voldoent aan de eigenschap, waarbij d(X1, l) = a
en d(X1, m) = b. Stel XX1 snijdt l, m opvolgend in P en Q, waarbij X1P = p en X1Q = q. Dan is PX = kp en QX = kq. Voor PQ hebben we dan PQ = X1P - X1Q = XP - XQ of p - q = kp - kq = k(p-q) Wegens k � 1 is dus c = d; maw. P valt samen met Q. Dus de lijn XX1 gaat door S. � |
| Opmerking Door de keuze van de lijnen l' en m' aan een andere kant van l; en/of m', vinden we de overige drie halve lijnen door S die de rest van de meetkundige plaats vormen. [einde Opmerking] |
| Definitie Twee lijnen l en m heten isogonaal verwant tov. een hoek S, als ze door S gaan �n elkaars spiegelbeeld zijn in de bissectrice van die hoek S (zie figuur 3). |
| . |
Bewijs: zie figuur 3.
| figuur 3 | 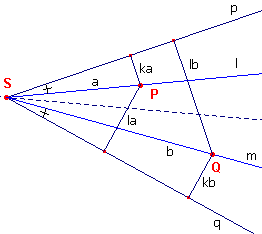 |
l is een lijn als in stelling 1. Voor elk punt van l is er dus een vaste verhouding van de afstanden tot p en q. Stel deze verhouding is k : l. Stel nu SP = a; dan is d(P,p) = ka en d(P,q) = la. m is eveneens een lijn als in stelling 1. Vanwege de symmetrie tov de bissectrice, bestaat op deze lijn dezelfde verhouding. Stel SQ = b; dan is d(Q,p) = lb en d(Q,q) = kb. Beide producten ka � lb en la � kb zijn dus aan elkaar gelijk.� |
| Stelling 3a [3a.1] Als drie hoektransversalen van driehoek (waarvan �en in elk hoekpunt) concurrent zijn, dan zijn de isogonaal-verwanten daarvan eveens concurrent. [3a.2] De voetpuntscirkels van twee isogonaal verwante punten (zie Opmerking 1) van een driehoek vallen samen. |
| figuur 4.1 | 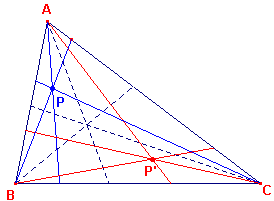 |
[3a.1] zie figuur 4.1 Het bewijs volgt uit stelling 2 en de stelling van Ceva. � Klik hier
Opmerkingen |
[2]
Elk punt van een zijde van de driehoek (niet zijnde een hoekpunt) is isogonaal verwant
met het overstaande hoekpunt van die zijde.
[einde Opmerkingen]
| figuur 4.2a | 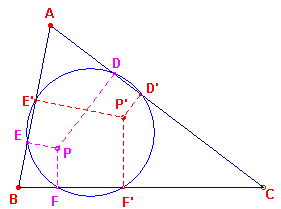 |
[3a.2] zie figuur 4.2a De driehoeken BPE en BP'F' zijn gelijkvormig, immers �PBE = �P'BF' terwijl beide driehoeken een rechte hoek hebben. Dus: BE : BF' = PE : P'F' of PE . BF' = P'F' . BE .....(1) De driehoeken BPF en BP'E' zijn gelijkvormig, waaruit volgt BF : BE' = PF : P'E' of PF . BE' = P'E' . BF .....(2) Uit stelling 2 volgt PE . P'E' = PF . P'F' .....(3) |
Uit (1), (2) en (3) volgt door vermenigvuldiging en deling:
BE . BE' = BF . BF'
De punten E, E' , F, F' liggen dus op een cirkel c1.
Op dezelfde manier bewijzen we, dat F, F', D, D' op een cirkel c2 en D, D', E,
E' op een cirkel c3 liggen.
Stel c1 en c2 zijn verschillend. Ze gaan beide door F, en F'.
De machten van A ten opzichte van beide cirkels zijn dan gelijk. A ligt dan op de
machtlijn, BC, van c1 en c2. Tegenspraak.
De cirkels c1 en c2 (en ook c3) vallen dus samen. �
Opmerkingen
[1]
Het middelpunt van de voetpuntscirkel is het midden van PP'.
Immers:
D en D' op de cirkel. Middelpunt ligt op de middelloodlijn van DD'.
E en E' op de voetpuntscirkel. Middelpunt ligt op de middelloodlijn van EE'.
In de rechthoekige trapezia PP'D'D en PP'E'E zijn die middelloodlijnen middenparallellen
van de opstaande zijde.
Beide middelloodlijnen gaan dus door het midden van PP'.
| Gevolg van Opmerking 1 De isogonaal geconjugeerde P' van een punt P tov. een driehoek ABC is het middelpunt van de cirkel door de gespiegelden van P in de zijden van die driehoek. |
Bewijs:
| figuur 4.2b | 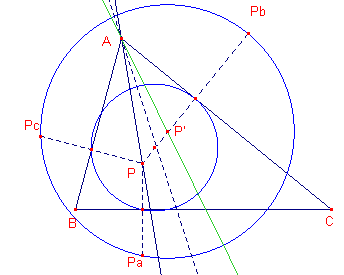 |
Zij M het midden van PP'. Zijn verder Pa, Pb, Pc de spiegelbeelden van P
in de zijden van driehoek ABC. M is dus het middelpunt van de voetpuntscirkel van de punt P en P (zie Opmerking 1 hierboven). We beschouwen nu de vermenigvuldiging met centrum P en factor 2. Hierdoor gaat deze cirkel over in de cirkel door Pa, Pb, Pc. Het punt M gaat daardoor over in P'. P' is dus het middelpunt van die laatste cirkel � |
[2]
Stelling 3.2 wordt op de pagina "Cirkels
van Droz-Farny" op een iets andere manier bewezen.
[3]
Zie ook de pagina "Oppervlakte van voetpuntsdriehoeken"
[4]
Zie ook Stelling 4 op de pagina "Meer
over isogonale verwantschap"
[einde Opmerkingen]
Gevolg
Kiezen we het punt P als hoogtepunt, dan weten we dat de cirkel
van Feuerbach (negenpuntscirkel) de voetpuntscirkel van P is.
Deze cirkel gaat ook door de middens van de zijden van de driehoek.
Dus:
| Stelling 3b Het hoogtepunt H en het middelpunt M van de omgeschreven cirkel van een driehoek zijn isogonaal verwante punten van die driehoek. |
Klik hier ![]() voor een animatie
van deze eigenschap.
voor een animatie
van deze eigenschap.
Tweede bewijs:
We kunnen dit ook direct afleiden uit de hoek die de hoogtelijn uit een hoekpunt en de
middellijn van de omgeschreven cirkel door dat hoekpunt met de zijden van de driehoek
maken. Zie figuur 4.3.
| figuur 4.3 | 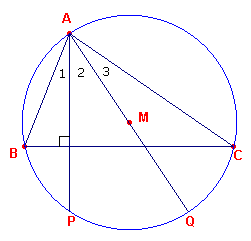 |
Hierin is:
Opmerking |
| Stelling 3c Het beeld van de omcirkel van driehoek ABC bij een isognale afbeelding is de oneigenlijke rechte. |
Bewijs:
| figuur 4.4 | 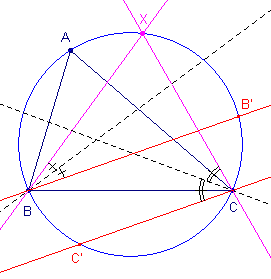 |
In de figuur is ABX = ACX (omtrekshoeken op dezelfde cirkelboog). Wegens de spiegelingen van XB em XC in de bissectrices (met beelden BB' en CC') hebben we B'BC = C'CB waaruit evenwijdigheid van de lijnen BB' en CC' volgt. Het isogonaalbeeld van X is dus het oneigenlijke punt van BB' en CC'. De omcirkel wordt dus afgebeeld op de oneigenlijke rechte. � |
| Definitie Twee lijnen l en m heten antiparallel ten opzichte van de lijnen p en q, indien er twee lijnen l' (// l) en m' (// m) zijn die met p en q isogonaal verwant zijn (zie figuur 5). |
| figuur 5 | 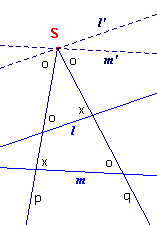 |
In plaats van "antiparallel ten opzichte van p en q"
spreekt men ook wel van "antiparallel ten opzichte van hoek S", als S het
snijpunt is van de lijnen p en q. Nb. |
| Opmerkingen [1] Het begrip "antiparallel" wordt in een enkel geval gebruikt om te bewijzen dat twee lijnen evenwijdig zijn. Bij inversie is de lijn door twee punten P en Q antiparallel met de lijn door de beeldpunten P' en Q' (zie figuur X). Een bewijs als bedoeld in de eerste zin kan dus vaak van pas komen bij gebruik van inversie (zie Inversie en de Stelling van Feuerbach). [2] Zie ook het Cabri-werkblad "Parallel en antiparallel" [einde Opmerking] |
figuur 6 | 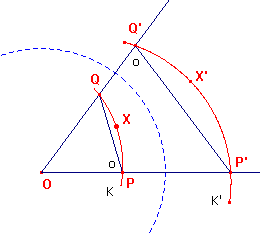 |
| Stellling 4a De zijden van de voetpuntsdriehoek van de hoogtelijnen van een driehoek zijn antiparallel met de zijden van de driehoek |
Bewijs: zie figuur 7.
| figuur 7 | 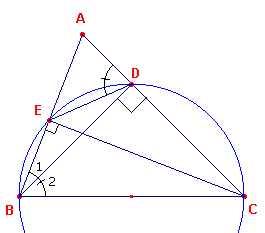 |
In deze figuur zijn BD en CE hoogtelijnen. Nu is BCDE een
koordenvierhoek, immers BDC = CEB = 90�. In deze koordenvierhoek is dus B + EDC = 180�. B = 180� - EDC = EDA. Waaruit het gestelde voor DE en BC (tov. hoek A) volgt. Op dezelfde manier wordt eea. bewezen voor de andere zijden van de voetpuntsdriehoek. � |
| Stelling 4b De inwendige raaklijnen aan twee cirkels zijn antiparallel tov. de hoek tussen de beide uitwendige raaklijnen. |
Bewijs: zie figuur 8.
| figuur 8 | 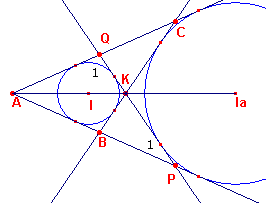 |
In figuur 8 zijn de gemeenschappelijke raaklijnen aan I en Ia
(van driehoek ABC) getekend. Vanwege de symmetrie (in AIa) geldt: � P1 = � C Dus BC en PQ antiparallel zijn (tov. hoek A). � |
Voor de behandeling van het punt van Lemoine zijn de volgende eigenschappen van belang.
| Definitie De isogonaal-verwante van een zwaartelijn (mediaan) van een driehoek heet symmediaan van die driehoek.(zie figuur X). |
| . |
| Stelling 5 [1] Een symmediaan verdeelt de overstaande zijde in stukken die zich verhouden als de kwadraten van de opstaande zijden. [2] De afstanden van een punt van die symmediaan tot de opstaande zijden verhouden zich als die opstaande zijden. [3] Een symmediaan gaat door het midden van een lijnstuk dat antiparallel is met de overstaande zijde. |
Bewijs:
| figuur 9.1 | 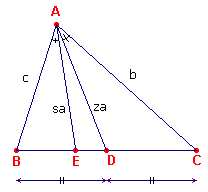 |
[1] zie figuur 9.1. De symmediaan uit A snijdt BC in het punt E. We dienen nu te bewijzen, dat BE : CE = c2 : b2 Zij D het midden van BC. Dan is
|
||||||||||||
| figuur 9.2 | 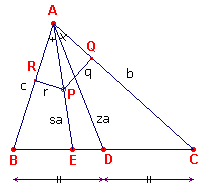 |
[2] zie figuur 9.2 F(ACE) / F(ABE) = CE / BE = b2 / c2 (zie stelling 5.1) F(ACE) = � qb � k met k = AE/AP F(ABE) = � rc � k qb / rc = b2 / c2, waaruit dus q / r = b / c � Opmerking |
||||||||||||
| figuur 9.3 | 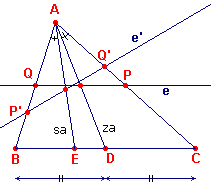 |
[3] zie figuur 9.3. De lijn e (evenwijdig aan BC) snijdt de opstaande zijden in P en Q. De lijn za gaat door het midden van PQ. Spiegeling van za in de bissectrice van hoek A samen met driehoek APQ geeft sa met driehoek AQ'P'. Nu is in driehoek AQ'P': � Q' = � Q (in driehoek APQ) = � B. De symmediaan van A gaat dus door het midden van P'Q' die antiparallel is met BC (tov. hoek A). � |
Overzicht
| Stelling 6 De symmedianen van een driehoek gaan door ��n punt. Dit punt heet het symmediaanpunt of het punt van Lemoine (Emile Lemoine, 1840-1912, Frankrijk) van die driehoek, en wordt meestal aan gegeven met K. |
Zie ook de pagina "Barycentrische co�rdinaten"
Bewijs: zie figuur 10.
| figuur 10 | 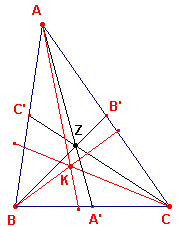 |
Dit volgt onmiddellijk uit de definitie van symmediaan en stelling
3; immers de zwaartelijnen van een driehoek zijn concurrente hoektransversalen (dit
laatste is weer een gevolg van de stelling van Ceva). � Opmerkingen |
[3]
Er bestaat ook een cirkel van Lemoine. Deze cirkel (de eerste
cirkel van Lemoine) speelt een rol bij het verband tussen het punt van Lemoine, een Miquel-punt en de punten van Brocard.
Klik hier voor een beschrijving van dat
verband.
Een algemene behandeling van de beide Lemoine-cirkels
wordt gegeven op de pagina "Tucker-cirkels".
De beide Lemoine-cirkels komen ook aan de orde op het Cabri-werkblad "Parallel en antiparallel".
| Stelling 7 Het punt van Lemoine van een rechthoekige driehoek is het midden van de de hoogtelijn op de hypothenusa. |
Bewijs: zie figuur 11.
| figuur 11 | 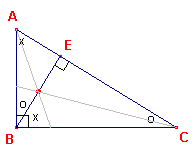 |
In de rechthoekige driehoek is BE antiparallel met BC (tov hoek A). sa gaat door het midden van BE (zie stelling 5.3). Maar ook: BE is antiparallel met AB (tov. hoek C). sc gaat door het midden van BE. Het midden van BE is dus het punt van Lemoine van de rechthoekige driehoek.� |
Klik hier ![]() voor een animatie
van deze eigenschap.
voor een animatie
van deze eigenschap.
| Stelling 8 De voetpuntsdriehoek van het punt van Lemoine heeft dat punt als zwaartepunt. |
Bewijs:
We zullen voor deze stelling twee bewijzen geven (klik
hier voor het 2e bewijs).
1e bewijs: zie figuur 12.
| figuur 12 | 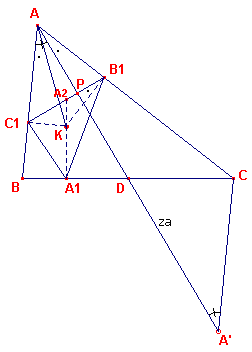 |
De punten A1, B1, C1 vormen de
voetpuntsdriehoek van K (het punt van Lemoine van driehoek ABC). Het punt P is het snijpunt van za (= AD) met B1C1. AC1KB1 is een koordenvierhoek met middellijn AK. Dus: � AB1C1 = � AKC1 (staan op gelijke bogen). AK = sa, dus � C1AK = � B1AP. De driehoeken AKC1 en AB1P hebben dus twee hoeken gelijk; dus ook de derde: � C1 = � P = 90� . De lijn AD snijdt de lijn door C evenwijdig aan AB in het punt A'. Nu is driehoek ACA' ~ driehoek B1KC1 (hh), immers � KB1C1 staat op de boog KC1, waarop ook hoek AC1K staat) (zie ook Opmerking). Verder is CD zwaartelijn van driehoek ACA'. Voor deze gelijkvormige driehoeken geldt nu |
Dus is A1A2 (A2 is het snijpunt van A1K met
B1C1) een zwaartelijn van driehoek A1B1C1.
Evenzo geldt dit voor B1K en C1K.
K is dus zwaartepunt van driehoek A1B1C1. �
Opmerkingen
[1]
Uit de gelijkvormigheid van de driehoeken ACA' en B1KC1 volgt ook:
CA' : KC1 = AC : B1K of
c : KC1 = b : B1K
zodat
KB1 : KC1 = b : a
waarmee we op een andere manier stelling 5.2 bewezen hebben.
[2]
Zie ook Hulpstelling 7 op de pagina "Meer over isogonale verwantschap"
[einde Opmerking]
| figuur 13 | 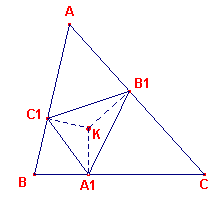 |
Volgens stelling 5.2 geldt voor de afstanden van het
punt K tot de zijden van de driehoek KA1 : KB1 : KC1 = a : b : c Er is dus een factor p zodat KA1 = pa, KB1 = pb en KC1 = pc. Voor de oppervlakte F van driehoek KB1C1 geldt dus: F = �KB1.KC1.sin(180�-a) = �p2bc.sin(a) = p2O. Hierin is O de oppervlakte van driehoek ABC De oppervlakte F is dus onafhankelijk van B1 en C1. Dus hebben de driehoeken KB1C1, KA1C1 en KA1B1 gelijke oppervlaktes. Dus is K het zwaartepunt van driehoek A1B1C1. � |
Gevolg
Uit dit tweede bewijs kunnen we de factor p bepalen. Immers
O = �KA1.a + �KB1.b + �KC1.c
= �p(a2 + b2 + c2), zodat
p = 2O / (a2 + b2 + c2)
Zie ook de pagina "De constructie en de stelling van Grebe".
Hiermee samenhangend kunnen we ook nog bewijzen:
| Stelling 9 Het punt waarvoor de som van de kwadraten van de afstanden tot de zijden van een driehoek minimaal is, is het punt van Lemoine van die driehoek. |
Bewijs:
Voor het punt X met afstanden x, y, z tot de zijden a, b, c van een
driehoek met oppervlakte O geldt
2O = ax + by + cz
Gemakkelijk is na te gaan dat de volgende identiteit van Lagrange (Joseph-Louis Lagrange, 1736-1813, Itali�/Frankrijk)
geldt
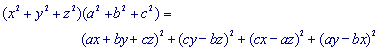
Hieruit volgt onmiddellijk:
![]()
waarbij het gelijkteken alleen geldt als x : y : z = a : b : c (drie
laatste termen gelijk aan 0).
Dus als X samenvalt met het punt van Lemoine van de driehoek, is de waarde van x2 + y2 + z2
minimaal. �
Opmerking
Zie ook de pagina "Barycentrische co�rdinaten"
[einde Opmerking]
| Stelling 10 K is het snijpunt van de lijnen die de polen van de zijden tov. de omgeschreven cirkel verbinden met het overstaande hoekpunt OF De symmedianen van een driehoek gaan door de polen van de zijden tov. de omgeschreven cirkel. |
Bewijs: zie figuur 14.
| figuur 14 | 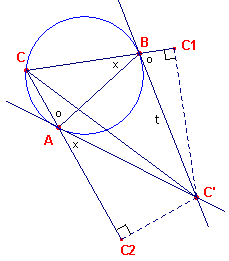 |
C' is de pool van de zijde AB. t is de lengte van het raaklijnstuk uit C' aan de omgeschreven cirkel.. C1 en C2 zijn de projecties van C' op de zijden Bc en AC. Nu is sin A = C'C1/ t en sin B = C'C2 / t (zie de bogen van de omtrekshoeken). Dus: C'C1 : C'C2 = sin A : sin B = a : b C' ligt dus op de symmediaan van C (zie stelling 5.2). Analoog kan dit bewezen worden voor de polen A' en B'. Waarmee het gestelde is aangetoond. � |
Lemoine-cirkels
Op het Cabri-werkblad "Parallel en
antiparallel" worden de beide Lemoine-cirkels behandeld.
Deze cirkels hangen ten nauwste samen met de parallellen en antiparallelen
van de zijden van een driehoek.
| figuur 15 | figuur 16 |
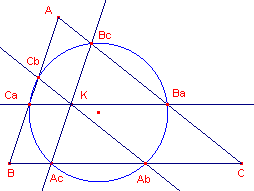 |
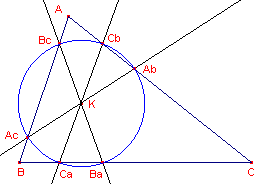 |
| Eerste Lemoine-cirkel | Tweede Lemoine-cirkel |
De Lemoine-cirkels zijn twee cirkels uit een klasse van cirkels, de zogenoemde Tucker-cirkels.