Twee raaklijnen aan een ellips; orthoptische cirkel
Overzicht ][ Anal. meetkunde | Kegelsneden | Meetkunde
1.
Hoofdeigenschap van de raaklijn aan een ellips ![]()
| Stelling 1 De raaklijn in een punt van een ellips is bissectrice van de buitenhoek van de hoek tussen de brandpuntsvoerstralen naar dat punt. |
| figuur 1 | 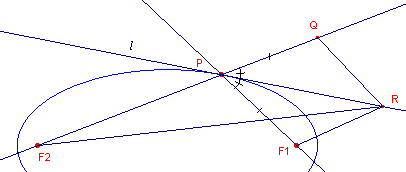 |
We weten dat PF1 + PF2
= 2a (definitie van een ellips, met 2a = lengte van de grote as). Zij l de bissectrice van de bedoelde hoek. We bewijzen nu dat l raakt aan de ellips. Kies op het verlengde van F2P het punt Q zo, dat PQ = PF1. Kies R op l (met R � P). Nu is PQR congr PF1R (ZHZ), zodat RF1 = RQ. Zodat RF1 + RF2 = RQ + RF2 > QF2 (driehoeksongelijkheid in driehoek RQF2). Tenslotte, RF1 + RF2 > 2a, omdat QF2 = 2a. |
Het punt R ligt dus niet op de ellips.
P is het enige punt van de lijn l dat op de ellips ligt. l raakt dus in
P aan de ellips. �
| Gevolg Het spiegelbeeld Q van het punt F1 in de raaklijn in P ligt op het verlengde van PF2 met QF2 = 2a. |
Klik hier ![]() voor een
CabriJava-applet gebaseerd op het bovenstaande.
voor een
CabriJava-applet gebaseerd op het bovenstaande.
2. Raaklijnen uit
een punt ![]()
We kunnen een bijzondere meetkundige eigenschap bewijzen als we in twee
verschillende punten van de ellips de raaklijnen beschouwen.
Zijn R1 en R2 de raakpunten. De
raaklijnen in R1 en R2 snijden elkaar
in het punt P.
Zij G1 en G2 de spiegelbeelden van F1
en F2 in de raaklijnen (zie figuur 2).
| figuur 2 | 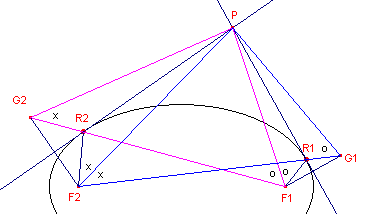 |
Bewijs: |
Voor de zijden van de driehoeken PF1G2
en PG1F2 geldt verder: PF1
= PG1 en PG2 = PF2,
zodat beide driehoeken congruent zijn (ZZZ). De hoeken bij P in deze driehoeken zijn dus
gelijk.
Beide hoeken hebben het hoekdeel F1PF2
gemeenschappelijk, zodat
�F1PG1
= �F2PG2.
�
Opmerking. Zie ook Isogonaal-eigenschappen.
Klik hier ![]() voor een
CabriJava-applet gebaseerd op het bovenstaande.
voor een
CabriJava-applet gebaseerd op het bovenstaande.
Gevolgen
[1]
�PG1F2 = �PF1G2 (zie figuur 2) ......(1)
Maar vanwege de symmetrie in de raaklijn in R1: �PF1R1 = �PG1F2 ......(2)
(1) en (2) geven dan:
| PF1 is de bissectrice van de hoek tussen de brandpuntsvoerstralen vanuit F1 naar R1 en R2. |
[2]
Constructie van de raaklijnen ![]()
| figuur 3 | 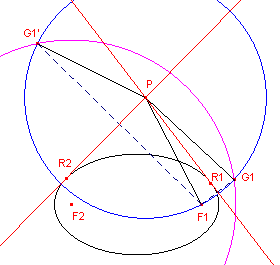 |
Doordat het punt G1 op het verlengde ligt van
de lijn F2R1 (zie figuur
2), ligt G1 dus ook op de richtcirkel van de ellips met
middelpunt F2. Een richtcirkel van de ellips is de cirkel met middelpunt F2 (cq. F1) en straal 2a (de lengte van de grote as; zie ook de pagina "Ellipsconstructie 4b"). Hieruit kan een constructie van de raaklijnen uit P aan de ellips worden afgeleid. In figuur 3 snijdt de cirkel (P, PF1) de richtcirkel in de punten G1 en G1'. De middelloodlijnen van de lijnstukken F1G1 en F1G1' (die uiteraard door P gaan) zijn nu de raaklijnen aan de ellips. |
Klik hier ![]() voor een
illustratie van deze constructie.
voor een
illustratie van deze constructie.
3. Orthoptische
cirkel ![]()
Zij nu �R1PR2
= 90�.
We hebben dan een rechte "kijkhoek" vanuit P tov. de ellips.
| Stelling 3 De meetkundige plaats van de punten met een rechte kijkhoek tov. een ellips is een cirkel met als middelpunt het middelpunt van de ellips en als straal �(a2 + b2), waarin a en b de lengtes zijn van de halve assen van de ellips. De cirkel heet orthoptische cirkel van de ellips. |
| figuur 4 | 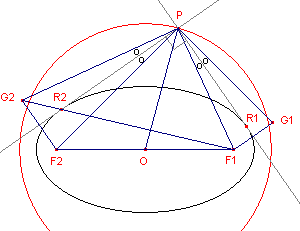 |
We weten F1F22
= (2c)2 = 4c2. Nu is PO2 = � PF12 + � PF22 - � F1F22 (zwaartelijnformule in driehoek PF1F2), of PO2 = � (PF12 + PF22) - c2 Verder is ook �F1PG2 = 90�, zodat in driehoek F1PG2 geldt: PF12 + PG22 = F1G22 =(2a)2 = 4a2. En dus, wegens PF2 = PG2, PF12 + PF22 = 4a2. Voor PO2 hebben we dan: PO2 = �(4a2) - (a2 - b2) = a2 + b2. � |
Opmerking
De orthoptische cirkel wordt ook wel cirkel van Monge genoemd (naar Gaspard Monge, 1746-1818, Frankrijk)
[einde Opmerking]
Klik hier ![]() voor een
CabriJava-applet gebaseerd op het bovenstaande.
voor een
CabriJava-applet gebaseerd op het bovenstaande.
� Zie ook Referenties [1].
4.
Isogonaal-eigenschappen ![]()
Zie figuur 4. Uit die figuur blijkt dat �F1PG1
= �F2PG2.
Maar dan geldt ook:
�F1PR1
= �F2PR2 ......(3)
immers de beide raaklijnen zijn middelloodlijnen in de driehoeken F1PG1
en F2PG2.
Maar (3) wil niets anders zeggen, dan dat de raaklijnen in R1 en R2 isogonaal verwant zijn met de lijnen PF1
en PF2.
| [1] | DICK KLINGENS, De orthoptische cirkel van een ellips (de Monge-cirkel), PDF-bestand (ca. 115 Kb), 31 jan. 2007 | |
| [2] | P. MOLENBROEK, Leerboek der Vlakke Meetkunde, P. Noordhoff N.V., Groningen (1924) | |
| [3] | J.G. RUTGERS, Beknopte Analytische Meetkunde, P. Noordhoff N.V., Groningen (1946) | |
| [4] | J. VERSLUYS, Meetkunde der kegelsneden, A. Versluijs, Amsterdam (1909) |
[orthopt.htm] laatste wijziging op:29-03-07