Cabri-werkblad
Overzicht ][
Alle werkbladen | Meetkunde | Cabri
0. Overzicht - Isogonaalafbeelding 
- Afbeeldingen
van het vlak op zichzelf
- De constructiestappen
Opdracht
1 / Opdracht 2
- Macro en meer
Opdracht
3 / Opdracht 4 / Opdracht 5 / Opdracht
6
- Een isogonaalafbeelding is
anders!
Opdracht
7
- Oneigenlijk punt en
oneigenlijke rechte
Opdracht
8 / Opdracht 9 / Opdracht 10
- Verder onderzoek
Opdracht
11 / Opdracht 12
- Tenslotte
Opdracht 13
- Referenties
- Download
1. Afbeeldingen van het
vlak op zichzelf 
De punten in het vlak vormen een verzameling. Bekende afbeeldingen die deze verzameling op
zichzelf afbeelden, zijn onder meer de (lijn)spiegeling en de rotatie (draaiing).
Elk punt (elke figuur) heeft bij een dergelijke afbeelding een beeldpunt (beeldfiguur); zie figuur 1.
| figuur 1a |
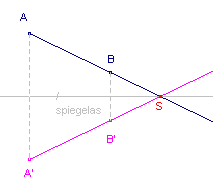 |
figuur 1b |
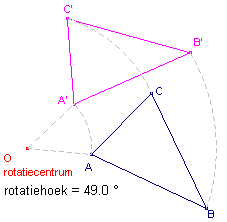 |
Bij dit type afbeeldingen zijn er ook punten die op zichzelf worden afgebeeld (men
noemt ze wel eens dekpunten):
- bij de lijnspiegeling: alle punten van de spiegelas (zie het punt S dat op het verlengde
van AB ligt);
- bij de rotatie: het centrum O van de rotatie (en als de rotatiehoek een veelvoud is van
360� zelfs alle punten).
Bij bovenstaande meetkundige afbeeldingen kunnen we het beeldpunt van een punt (of een
figuur) natuurlijk construeren met behulp van de betreffende Cabri-functie (in het Afbeeldingen-menu).
Het aantal afbeeldingen dat standaard in Cabri is opgenomen, is evenwel beperkt.
Als we een ander type afbeelding (niet-standaard) willen gebruiken, dan moeten we die door
middel van een aantal constructiestappen vastleggen.
We zullen dat hieronder doen voor de isogonale afbeelding.
Hebben we bij de lijnspiegeling "als basis" een rechte lijn (de spiegelas), bij
de rotatie bestaat de basis uit het centrum van de rotatie en de rotatiehoek.
Bij de isogonale afbeelding is de basis een driehoek.
2. De constructiestappen

We gaan dus uit van een driehoek ABC. Bekijk nu de onderstaande figuur (figuur
2) goed.
| figuur 2 |
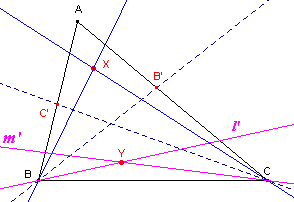 |
Hierin is:
| - |
X een willekeurig punt; |
| - |
BB’ en CC’ zijn de bissectrices van de hoeken B en C; |
| - |
l’ is het spiegelbeeld van BX in BB’ en m’
is het spiegelbeeld van CX in CC’; |
| - |
Y is het snijpunt van de lijnen l’ en m’. |
|
We spreken nu af te zeggen:
Y is het beeld van X bij de isogonale afbeelding ten opzichte van driehoek ABC.
Ook wel:
Y is het isogonaalbeeld van X (ten opzichte van de driehoek) of X en Y zijn isogonale
punten (zie Opdracht 1b).
Opdracht 1

| a. |
Voer bovenstaande constructies ook zelf
met Cabri uit.
Teken daarbij de driehoek met behulp van de functie "Driehoek" in het Teken-menu. |
| b. |
Is X het beeld van Y bij deze isogonale afbeelding?
Verklaar je antwoord. |
Opdracht 2

| a. |
Ga na, dat je de beeldpunten van A, B en C niet op deze
manier kunt vinden.
Waarom niet? |
| b. |
Ga na, dat elk punt van de zijde BC van de driehoek wordt
afgebeeld op het punt A.
Geef een korte toelichting. |
| c. |
Op welk punt wordt het snijpunt van BB’ en CC’
afgebeeld? |
3. Macro en meer

Uitgaande van de figuur die je in Opdracht 1 gemaakt
hebt, kunnen we een macro vastleggen, waarmee we van een punt X (niet zijnde een hoekpunt
van de basisdriehoek) direct het isogonaalbeeld X’ tov. de driehoek ABC kunnen
tekenen.
Opdracht 3

Leg de macro:IsogonaalBeeld vast. Je kan daarbij de
constructie als in figuur 2 gebruiken.
Beginobjecten: punt X en driehoek ABC
Eindobjecten: punt Y
Bewaar de macro, ook voor eventueel later gebruik, in een bestand.
Opdracht 4

Ga uit van een nieuw werkblad en teken daarop (met de functie
"Driehoek") driehoek ABC.
Kies een willekeurig punt A’ op de zijde BC van driehoek ABC ("Op deze
driehoek").
Teken ook de lijn AA’. Kies op die lijn een punt X (met de functie "Punt op
object" in het Punt-menu).
Gebruik de macro:IsogonaalBeeld om het beeld X’ van X te construeren.
Wat gebeurt er nu met X’ als je het punt X op de lijn verplaatst naar A’?
Is dit in overeenstemming met Opdracht 2b?
Wat gebeurt er met X’ als je punt X verplaatst naar A?
Onder welke voorwaarde ligt het punt X’ ook op de lijn AA’?
Opdracht 5

We zouden nu op basis van hetgeen gevonden is in Opdracht 4,
het volgende kunnen afspreken:
het isogonaalbeeld van een hoekpunt van de basisdriehoek is
…… .
Kan je nu bovenstaande zin aanvullen?
Maar, … .
Is er mogelijk een "maar" aan je antwoord verbonden?
Opdracht 6

Kan je nu al zeggen of er rechte lijnen zijn die door de
isogonaalafbeelding op zichzelf worden afgebeeld?
"Op zichzelf" betekent hier dat het beeld van de lijn samenvalt met het
origineel, maar het hoeft niet in te houden dat elk punt van zo’n lijn dan ook
dekpunt is.
Zo ja, geef dan een korte toelichting (voorbeelden).
Aanwijzing
Kijk nog eens naar wat je gevonden hebt in Opdracht 4.
4. Een isogonaalafbeelding is anders!

Bij de standaard afbeeldingen (zoals de genoemde lijnspiegeling en de
rotatie) weten we dat de beelden van rechte lijnen (of lijnstukken) weer recht zijn en dat
de beelden van bijvoorbeeld cirkels ook cirkels zijn.
Dat is echter niet het geval bij de isogonaalafbeelding. Kijk maar eens naar figuur 3, waarin het beeld van het lijnstuk PQ is weergegeven.
| figuur 3 |
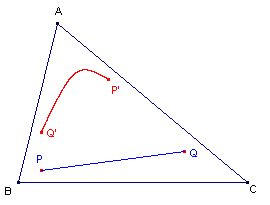 |
Opdracht 7

| a. |
Ga weer uit van een nieuw werkblad. Zorg ervoor, dat de
macro:IsogonaalBeeld geladen is.
Teken nu driehoek ABC en het lijnstuk PQ (zie figuur 3).
Construeer met de macro eerst de isogonaalbeelden P’ en Q’ van P en Q. |
We kunnen nu niet onmiddellijk het beeld van het lijnstuk PQ vinden, omdat de
isogonaalafbeelding via de macro puntsgewijs gedefinieerd is.
We nemen daarom onze "toevlucht" tot de functie "Meetkundige plaats"
in het Constructie-menu.
| b. |
Kies een punt X op het lijnstuk PQ (functie "Punt op
object" in het Punt-menu).
Construeer dan het isogonaalbeeld X’ van het punt X.
Kies dan de functie "Meetkundige plaats".
Selecteer nu eerst het punt X’ en daarna het punt X. |
Cabri tekent dan de meetkundige plaats van X’ als X het lijnstuk PQ doorloopt.
Deze meetkundige plaats is dus het beeld van het lijnstuk PQ onder de isogonaalafbeelding.
5. Oneigenlijk punt en oneigenlijke rechte

Het blijkt "handig" te zijn op elke rechte lijn een bijzonder
punt te denken: het zogenoemde oneigenlijk punt (ook wel "punt op
oneindig" genoemd) van die rechte lijn.
Twee evenwijdige lijnen hebben dan (per definitie) hetzelfde oneigenlijke punt.
De richting van die evenwijdige lijnen is hetzelfde; vandaar dat men een oneigenlijk punt
ook wel "identificeert" met een bepaalde richting.
De verzameling van alle oneigenlijke punten (richtingen) noemt men de oneigenlijke
rechte.
Met deze informatie vooraf kunnen we de volgende opdrachten uitvoeren.
| figuur 4 |
 |
Opdracht 8

| a. |
Kies een nieuw werkblad. Zorg ervoor dat ook de
macro:IsogonaalBeeld geladen is.
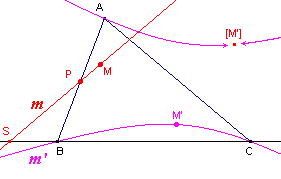
Teken op het werkblad een (niet al te grote) basisdriehoek ABC.
Kies een punt P op de zijde AB (zie figuur 4).
Teken door P een willekeurige lijn m.
Teken ook de lijn door de punten B en C.
m en de lijn BC snijden elkaar in S. |
| b. |
Neem nu een punt M op m en bepaal met de functie
"Meetkundige plaats" het beeld m’ van m bij de door driehoek
ABC bepaalde isogonaalafbeelding (zie figuur 4).
Waarom gaat m’ door de punten B en C?
Waarom gaat m’ door A?
Aanwijzingen
Verplaats het punt M op de lijn m en kijk naar de ligging van de punten M en
M’.
Welk punt is het isogonaalbeeld van het punt S? |
De meetkundige plaats -het beeld m’ van m- is op een bepaald
gedeelte onderbroken.
Dit wordt in figuur 4 aangegeven met twee pijlen.
Tussen beide pijlen zie je in figuur 4 nog een bijzonder punt,
[M’].
| c. |
Ga na, dat als je het punt M "voldoende ver" van
het punt P verwijdert, het punt M’ nadert tot dat onderbroken gedeelte. Je kan dit
bijvoorbeeld doen via de functie "Animatie" in het Extra-menu (het tweede
menu van rechts op de menubalk). |
We kunnen het onderbroken gedeelte nu als volgt verklaren.
Noem M
�
(uitgesproken als "M-bril" of "M-oneindig") het oneigenlijk punt van
de lijn m.
Als I de isogonaalafbeelding is die bepaald is door driehoek ABC, dan kunnen we
schrijven:
I(M) = M’
Nu geldt:
I(M� ) = [M’].
Cabri kan (helaas?) het punt M� niet bereiken, maar wel "bijna". Vandaar het onderbroken gedeelte.
Opmerking
Het isogonaalbeeld m’ van de lijn m is (in dit geval) een hyperbool.
We zullen dat hier evenwel niet bewijzen.
[Einde Opmerking]
figuur 5 |
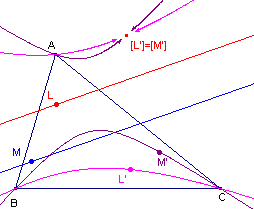 |
Opdracht 9

Kies een nieuw werkblad. De macro:IsogonaalBeeld moet ook beschikbaar zijn.
Teken een basisdriehoek ABC (zie figuur 5).
Teken ook twee punten (deze staan niet in figuur 5) en daardoor
twee evenwijdige lijnen l en m.
Ga na, dat I(L� ) en I(M� ) bij verschillende richtingen steeds samenvallen.
Opmerking
De punten L en M op de lijnen l en m zijn gebruikt om I(l) en I(m)
te construeren.
Opdracht 10

Kies een nieuw werkblad met daarop een basisdriehoek ABC.
Teken ook de omcirkel van de basisdriehoek (eventueel met de standaard macro:Omcirkel3P).
| figuur 6 |
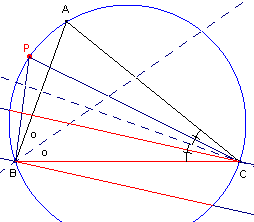 |
Het punt P is een punt van deze omcirkel (niet zijnde een
hoekpunt van de basisdriehoek).
Spiegel de lijn BP in de bissectrice van hoek B en spiegel de lijn CP in de bissectrice
van hoek C (zie figuur 6).
Bewijs dat deze spiegelbeelden evenwijdig zijn.
Wat is het isogonaalbeeld van de lijn BP? En van de lijn CP? |
Met andere woorden:
Het I-beeld van de omcirkel van de basisdriehoek is de oneigenlijke rechte.
6. Verder onderzoek

We zullen nu de omcirkel van de basisdriehoek bij ons verdere onderzoek
betrekken.
Opdracht 11

In het algemeen is het isogonaalbeeld van een rechte lijn een kegelsnede.
Zie ook de Opmerking na Opdracht 8.
| figuur 7 |
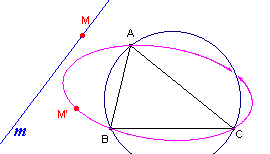 |
Nu we weten, dat beelden van de punten van de omcirkel van de basisdriehoek
oneigenlijke punten zijn, kunnen we het beeld van een lijn m nog eens nader
bekijken.
In figuur 7 snijdt de lijn m de omcirkel van de basisdriehoek niet.
We kunnen ook het beeld van de lijn m bekijken als m de omcirkel raakt of
snijdt.
Beschrijf in deze (drie) gevallen de gedaante van het isogonaalbeeld van de lijn m.
Opdracht 12

| figuur 8a |
 |
figuur 8b |
 |
| a. |
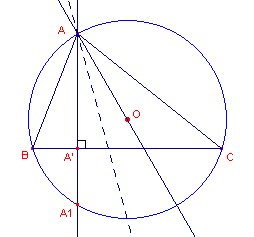
Bewijs, dat het spiegelbeeld van de hoogtelijn uit A in de
bissectrice van hoek A door het middelpunt van de omcirkel van de basisdriehoek gaat (zie figuur 8a). |
| b. |
Welk punt is dus het isogonaalbeeld van het
hoogtepunt H van de basisdriehoek ABC?
Licht je antwoord kort toe. |
| c. |
Welke punt is dan (dus) het isogonaalbeeld van het
middelpunt O van de omcirkel? |
De lijn door het hoogtepunt H en het middelpunt O van de omcirkel heet Euler-lijn
(ook wel lijn van Euler).
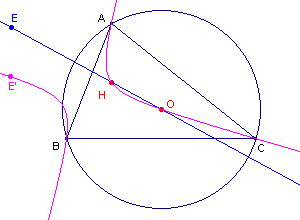
| d. |
Het isogonaalbeeld van de Euler-lijn is een hyperbool die
gaat door de punten H en O (zie figuur 8b).
Licht dit kort toe. |
7. Tenslotte

Blijkbaar levert elke rechte lijn die de omcirkel van de basisdriehoek
snijdt, als isogonaalbeeld een hyperbool op.
Een bijzondere rechte lijn is in dit geval de zogenoemde Brocard-as. Dit is de lijn
door het omcentrum O en het zogenoemde Punt van Lemoine (ook wel symmediaanpunt
genoemd) van de basisdriehoek. Vaak wordt dit laatste punt aangegeven met de
letter K.
Het punt van Lemoine is het isogonaalbeeld van het zwaartepunt Z van de basisdriehoek.
Het isogonaalbeeld van de Brocard-as is de Kiepert-hyperbool van de basisdriehoek.
| figuur 9 |
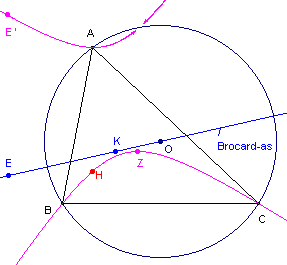 |
In deze figuur:
O is middelpunt van de omcirkel;
Z is zwaartepunt;
K is het punt van Lemoine (symmediaanpunt);
H is hoogtepunt;
E en E’ zijn punten die gebruikt zijn bij de constructie van het isogonaalbeeld van
de Brocard-as.
|
Opdracht 13

| a. |
Construeer met Cabri de Kiepert-hyperbool van driehoek ABC (zie figuur 9). |
Het vierde snijpunt van de omcirkel met de Kiepert-hyperbool (het
isogonaalbeeld van het punt op oneindig van de Brocard-as) heet Tarry-punt.
| b. |
Construeer ook het Tarry-punt van driehoek ABC. |
8. Referenties

| [1] |
|
Isogonale verwantschap, antiparellel, punt van Lemoine (webpagina) |
| [2] |
|
C. KIMBERLING, Triangle Centers and Central
Triangles, (TCCT), Winnipeg, Canada, 1998 |
| [3] |
|
Parallel en antiparallel (Cabri-werkblad) |
| [4] |
|
Probleem van Lemoine en de stelling van Kiepert (webpagina) |
9. Download

De Cabri-figuren op deze pagina zijn NIET MEER beschikbaar voor download.
Klik hier
om het downloaden te starten (ZIP-formaat, ca. 21Kb).
Deze pagina is NIET MEER beschikbaar in PDF-formaat.
 isogonw.pdf
(ca. 58Kb)
isogonw.pdf
(ca. 58Kb)

[isogonw.htm] laatste wijziging op:
19-01-18










