Overzicht - Parallel en
antiparallel ![]()
| figuur 1 | 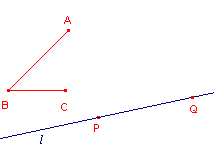 |
In figuur 1 bepalen de punten A, B en C een hoek.
Zoals in die figuur getekend, is de hoek ABC positief geori�nteerd, terwijl hoek
CBA negatief geori�nteerd is.
Er is ook een lijn l door het punt P getekend. Het punt Q ligt ook op l.
| a. | Hoeveel hoeken met P als hoekpunt zijn er, die
gelijk zijn aan hoek ABC en die l als been hebben? Maak op je antwoordblad een duidelijke schets. |
We willen nu, met P als hoekpunt en l als been, een hoek construeren die gelijk is aan hoek ABC, maar met dezelfde ori�ntatie als hoek ABC.
| b. | Hoeveel van dergelijke hoeken zijn er? Maak opnieuw een duidelijke schets. |
Tenslotte.
| c. | Hoeveel hoeken met dezelfde ori�ntatie als hoek ABC en met P als hoekpunt zijn er die QP als been hebben? |
| figuur 2 | 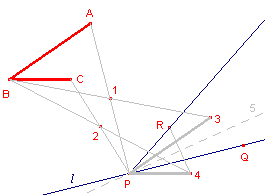 |
In figuur 2 is met Cabri een constructie uitgevoerd, gebaseerd op
figuur 1 en op Opdracht 1c.
De beschrijving van die constructie staat hieronder.
1 = Midden(A, P)
2 = Midden(C, P)
3 = Puntspiegeling(B, 1)
4 = Puntspiegeling(B, 2)
5 = Deellijn(3, P, Q)
R = Spiegeling(4, 5)
PR = HalveLijn(P, R)
De functies van Cabri zijn hier aangegeven als
Functie(X,Y), waarbij eerst het object X en daarna het object Y geselecteerd moet worden.| o. | Toon aan, dat hoek ABC gelijk is aan hoek RPQ. Aanwijzing Bekijk de in figuur 2 dik getekende lijnstukken (AB, BC, 3P, P4). |
| a. | Maak een macro:HoekNaarPunt voor de
constructie uit Opdracht 2, met Beginobjecten: C, B, A (de volgorde is belangrijk!), Q, P (ook hier is de volgorde belangrijk). Eindobjecten: PR ("Deze halve lijn"). |
Bewaar de macro in een bestand in verband een hierna volgende opdracht.
| b. | Leg kort uit waarom de volgorde C, B, A en de volgorde Q, P belangrijk is? |
Opmerking
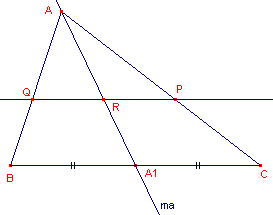
| figuur 3a | figuur 3b |
 |
 |
Teken een driehoek ABC met een punt P op de zijde AC (maak hierbij geen gebruik
van de functie "Driehoek" in het Teken-menu).
Teken ook de lijn door P evenwijdig met BC (Q op AB) en de zwaartelijn AA1 (zie figuur 3a).
| a. | Toon aan dat deze zwaartelijn (ma) het lijnstuk PQ in twee gelijk stukken (PR en QR) deelt. |
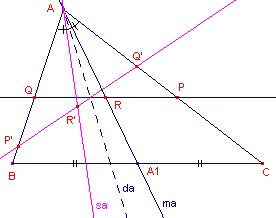
Teken nu ook de deellijn (bissectrice) da van hoek A (zie
figuur 3b).
Spiegel de lijnen PQ en AA1 in da (met de functie
"Spiegeling" in het Afbeeldingen-menu).
| b. | Toon nu aan dat het beeld P’Q’ van PQ in twee gelijke stukken verdeeld wordt door de lijn sa, die het beeld is van ma (in de spiegelas da). |
| c. | Toon ook aan, dat hoek P’Q’A gelijk is aan hoek ABC. |
Afspraken
Omdat PQ parallel is met BC, noemt men de lijn P’Q’ antiparallel
met BC.
Het beeld van een zwaartelijn (ook wel mediaan genoemd) bij spiegeling in de
bissectrice naar dezelfde zijde, noemt men een symmediaan van die zijde.
De resultaten van Opdracht 4 kunnen we nu (kort) formuleren als:
Een parallel van een driehoek wordt in twee gelijke stukken gedeeld door een mediaan
en
een antiparallel van een driehoek wordt in twee gelijke stukken gedeeld door een
symmediaan.
Opdracht 5 - Voetpuntsdriehoek
Teken een driehoek ABC en een punt P op de zijde AC.
Voer nu de macro uit (maar pas op): selecteer achtereenvolgens C, B, A, …
Je zou nu opnieuw A moeten selecteren (en dan P). Echter, Cabri staat twee keer
selecteren van een punt niet toe!
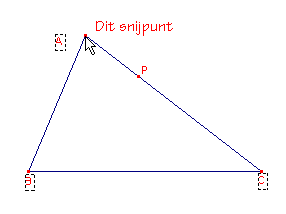
Je kan dat zien, als je de cursor in de buurt van A brengt. Je zou moeten krijgen
"Dit punt", maar je ziet "Dit snijpunt" (zie figuur 4a).
Als je toch klikt, gebeurt zeker er niet wat je wilt dat er gebeurt.
| figuur 4a | figuur 4b |
 |
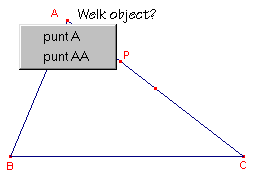 |
Je kan deze "onvolkomenheid" van Cabri echter omzeilen.
Construeer op de plaats van A nog een tweede punt (zie figuur 4b)!!
| a. | Beschrijf kort je hoe dat kan doen. Aanwijzing Er zijn meerdere mogelijkheden. Gebruik daartoe bijvoorbeeld het punt C (in figuur 4b staat een bijzonder punt op de zijde AC). |
Teken ook de lijn door P die antiparallel is met AB.
Geef P nu, indien nodig, een zodanige positie op AC, dat je de punten Q (op AB) en R (op
BC) kan bepalen (zie figuur 5).
| figuur 5 | 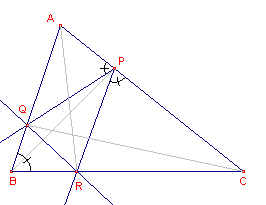 |
Teken ook de lijn QR.
| b. | Toon aan, dat QR antiparallel is met AC. Wat weet je nu van de driehoeken APQ, RBQ, RPC en ABC? |
Teken ook de lijnstukken AR, BP en CQ.
Verplaats P nu zo, dat deze lijnen door ��n punt gaan (zie figuur 6).
Klik hier ![]() voor een animatie
van deze eigenschap met CabriJava.
voor een animatie
van deze eigenschap met CabriJava.
| c. | Welke lijnen zijn AR, BP en CQ in dit geval van driehoek ABC? |
| . |
| figuur 6 | 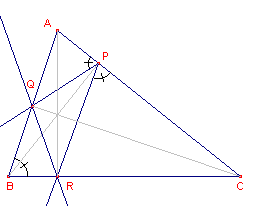 |
| . |
| d. | Toon aan dat in dit geval (bij de ligging van
P, als bedoeld in vraag c) hoek ARP = ARQ. Welke lijnen zijn AR, BP en CQ dus van driehoek PQR? |
Afspraak
| o. | Formuleer twee stellingen (een derde mag ook!) over de voetpuntsdriehoek van een driehoek. |
Opdracht 7 - Terug naar de symmedianen
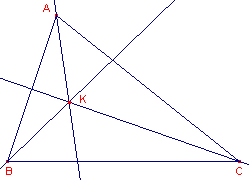
| a. | Waarom gaan de drie symmedianen door ��n
punt (zie figuur 7a)? Aanwijzing Ga na wat er met de lijnen aan de hand is die "originelen" zijn van die symmedianen. |
| Klik hier |
| figuur 7a | figuur 7b |
 |
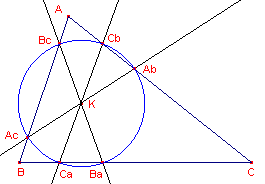 |
Teken nu door dat snijpunt, noem het K, de drie lijnen die antiparallel zijn met
de zijden van de driehoek (zie figuur 7b, waarin de symmedianen
zijn weggelaten).
Aanwijzing
Kijk eens in figuur 6. Daarin staan in ieder geval ook drie
antiparallellen.
| b. | Toon nu aan, dat de zes snijpunten van deze
lijnen met de zijden van de driehoek op een cirkel liggen. Aanwijzingen Wat weet je van het punt K? De letters bij de snijpunten duiden wellicht ook wel ergens op. |
Klik hier ![]() voor een animatie
van de cirkeleigenschap met CabriJava.
voor een animatie
van de cirkeleigenschap met CabriJava.
Opdracht 8 - Met een
uitdagend slot ![]()
Ga weer uit van het symmediaanpunt K (ook wel het punt van
Lemoine genoemd; naar Emile Lemoine, 1840-1912, Frankrijk).
| figuur 8 | 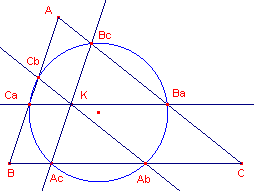 |
Teken nu de drie lijnen door K die parallel zijn met de zijden van de driehoek.
Ook nu liggen de zes snijpunten van die lijnen met de zijden van de driehoek op een
cirkel.
Klik hier ![]() voor een animatie
met CabriJava.
voor een animatie
met CabriJava.
Een uitdaging?
| o. | Construeer het middelpunt van de cirkel. Probeer te bewijzen, dat BcCb, AcCa en AbBa (in figuur 8) antiparallel zijn met de zijden van de driehoek. Probeer dan ook het bewijs te leveren van het feit, dat de zes punten op een cirkel liggen, en van de plaats van het middelpunt. |
Opmerking
Tenslotte ![]()
[1]
Op deze website zal ook een pagina worden gewijd aan de zogenoemde Tucker-cirkels.
De beide Lemoine-cirkels zijn namelijk bijzondere Tucker-cirkels.
Klik hier voor de pagina
"Tucker-cirkels".
[2]
Antiparallellen worden in samenhang met isogonalen in een driehoek
behandeld op de pagina "Isogonalen".
Download ![]()
De op dit werkblad gebruikte Cabri-figuren zijn NIET MEER te downloaden.
Deze pagina is NIET MEER beschikbaar in PDF-formaat.
![]() parenanti.pdf
[ca. 220 Kb]
parenanti.pdf
[ca. 220 Kb]