Zie ook de pagina "Punten van Brocard"
Zie ook de pagina "Verband tussen de punten van
Brocard, het punt van Lemoine en een punt van Miquel".
Zie ook het Cabri-werkblad "Koordenvierhoeken
en enkele stellingen van Miquel"
Opmerking - Met h(XOY) wordt op deze pagina de hoek XOY bedoeld; O is hoekpunt.
1. De stelling
![]()
In 1838 publiceerde Auguste Miquel (Frankrijk) de volgende fraaie stelling.
| figuur 1 | 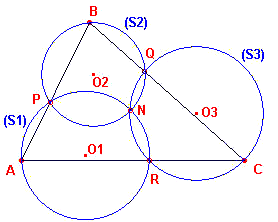 |
De verbindingslijnstukken AB, BC, CA vormen dus een driehoek. Klik
hier Klik hier voor het bewijs van Stelling 1. |
2. Punt van
Miquel ![]()
De omgekeerde stelling luidt:
We bewijzen eerst stelling 1 (zie figuur 1). Klik hier voor het bewijs van Stelling 2.
Bewijs: Zijn r1, r2, r3 en O1,
O2, O3 de stralen en middelpunten van S1, S2,
S3.
Het punt B kan verkregen worden uit A door een draaivermenigvuldiging met factor k1 =
r2/r1 en over h(O1NO2).; het punt C kan
verkregen worden uit B door een draaivermenigvuldiging met factor k2 = r3/r2
over h(O2NO3).
Is nu C' het beeld van C bij een draaivermenigvuldiging met factor k3 = r1/r3
over h(O3NO1). De som van deze drie draaivermenigvuldigingen is een
translatie, omdat
k1k2k3 = r2/r1 . r3/r2 . r1/r3 = 1
en h(O1NO2) + h(O2NO3) + h(O3NO1) = 360o.
Deze translatie voert elk punt A van de cirkel S1 dus over in een punt C' van
dezelfde cirkel. Dat wil dus zeggen dat S1 op zichzelf wordt afgebeeld. Dus C'
wordt uit A verkregen door de identieke afbeelding. Met andere woorden C' = A. ?
Stelling 1 kan eenvoudig worden uitgebreid tot een willekeurig
aantal cirkels die door hetzelfde punt gaan.
Dus, zoals in figuur 2, waarin we vier cirkels zien die elkaar in het
gemeenschappelijke punt N snijden.
| figuur 2 | 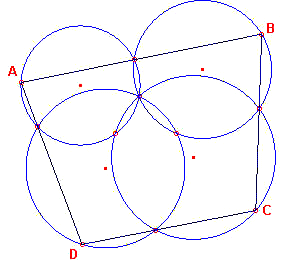 |
figuur 3a | 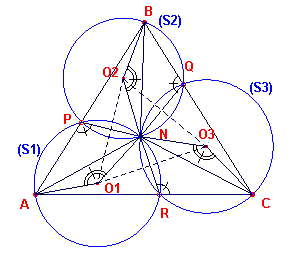 |
Klik hier ![]() voor een CabriJavapplet
van figuur 2.
voor een CabriJavapplet
van figuur 2.
Tenslotte geven we het bewijs van Stelling 2 (zie figuur 3a).
Bewijs van Stelling 2: Als driehoek PQR een
gelijkvormigheidstransformatie ondergaat, waarbij de hoekpunten zich bewegen over de
zijden AB, BC en CA van driehoek ABC, dan hebben alle posities van PQR een
gemeenschappelijk centrum van rotatie dat op de cirkels S1, S2, S3
ligt. Daarom gaan deze drie cirkels door ??n punt.
Vierhoek ARNP is een koordenvierhoek van S1.
Dus h(APN) + h(ARN) = 180o. Daaruit volgt dat
h(APN) = h(CRN).
Zo vinden we dat ook h(CRN) = h(NQB).
Dit heeft tot resultaat dat h(AO1N) = h(BO2N) = h(CO3N).
De gelijkbenige driehoeken AO1N, BO2N, CO3N zijn dus
gelijkvormig.
O1O2O3 kan dus uit ABC worden verkregen door een
draaivermenigvuldiging (met centrum N, hoek O1NA en factor NO1/NA). ?
Opmerkingen
[1]
Zie de paragraaf "Wat meer" voor een tweede
(eenvoudiger?) bewijs van Stelling 2.
[2]
Een bijzondere Miquel-configuratie wordt geleverd door de punten van
Brocard.
[3]
Er bestaat een verband tussen het Miquel-punt bij de punten van
Brocard en het punt van Lemoine van een driehoek.
Klik hier voor een beschrijving van dat
verband.
[4]
De stelling van Miquel kan als uitgangspunt dienen voor een
"elementair" bewijs van de stelling van Pascal (voor
cirkels).
Klik hier voor het downloaden
van een geZIPt Word document waarin bedoeld bewijs gebaseerd op koordenvierhoeken
en omtrekshoeken is opgenomen [ca. 38kB].
[einde Opmerkingen]
3.
Wat meer ![]()
3.1. Oneindig veel Miquel-configuraties
We kunnen bij elk punt P in het vlak van driehoek ABC meerdere
Miquel-configuraties vinden.
Klik hier ![]() voor een CabriJavapplet
waarin deze bewering kan worden onderzocht.
voor een CabriJavapplet
waarin deze bewering kan worden onderzocht.
| Stelling 3a Elk punt P bepaalt oneindig veel Miquel-configuraties bij een gegeven driehoek. |
Bewijs: zie figuur 3b.
| figuur 3b | 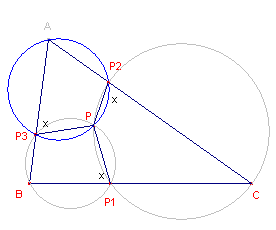 |
Bij gegeven P en variabele P1 op de zijde BC kunnen we P3
(op AB) en daarna P2 (op AC) construeren: eerst via de omcirkel van PBP1
(geeft het punt P3) en daarna de omcirkel van PAP3 (geeft P2). De aangegeven hoeken zijn gelijk. ? Een ander gevolg is weergegeven in Stelling 3b. |
|||||||
| figuur 3c | 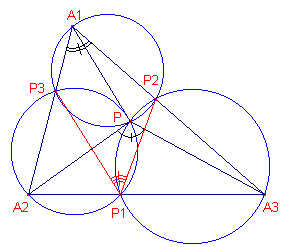 |
Bewijs: (het lijnstuk PP1 is niet getekend) Maar, met n(X) in de betekenis van nevenhoek van X,
|
| Stelling 3c Alle Miquel-driehoeken bij een gegeven Miquel-punt P zijn direct-gelijkvormig, waarbij P het gelijkvormigheidspunt is. |
Bewijs:
Uit Stelling 3b volgt direct, dat de hoeken van driehoek P1P2P3
onafhankelijk zijn van de ligging van de punten Pi; immers, A2PA3
is vast (bij vaste ligging van P); zo ook is A1. Dus ook P1;
enz.
Verder geldt: P2P3P = P2A1P =
A3A1P, waaruit volgt dat P gelijkvormigheidscentrum is.?
3.2. Een tweede bewijs van Stelling 2
![]()
We kunnen Stelling 2 ook bewijzen met de eigenschappen van de
koordenvierhoek .
Zie figuur 4.
| figuur 4 | 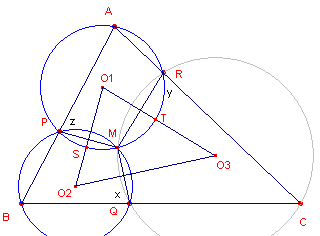 |
De punten P, Q, R liggen willekeurig op de zijden van driehoek ABC. O1 en O2 zijn de omcirkels van APR en BQP. Deze snijden elkaar nogeens in het punt M. We tonen nu aan, dat de punten CRMQ eveneens concyclisch zijn. We hebben ?BQM = x, ?CRM = y, ?APM = z. APMR is een koordenvierhoek: y = z. |
In koordenvierhoek APMR is ?A = ?bg PMTR.
De punten S en T zijn opvolgend de middens van de bogen PM en MT.
Dus ?O2O1O3 = bg SMT =
?bg PMTR = ?A.
Evenzo bewijzen we dat de andere hoeken van driehoek O1O2O3
gelijk zijn aan hoek B en koek C.
Driehoek O1O2O3 is dus gelijkvormig met driehoek ABC.
?
Opmerking
In het tweede bewijs van stelling 2 is gebruik gemaakt van het feit, dat het punt M binnen
driehoek ABC ligt.
Ook als M buiten de driehoek ligt (zie figuur 5), of als de punten P, Q,
R op het verlengde van de zijden liggen blijft de stelling gelden.
Klik hier ![]() voor een animatie van
het bovenstaande.
voor een animatie van
het bovenstaande.
| figuur 5 | 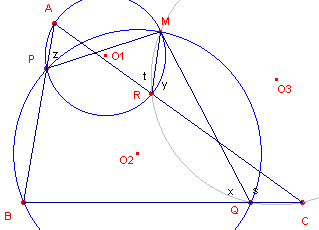 |
Nu is z = t en z = x, zodat x = t. s = 180? - x y = 180? - t zodat y = s. Waaruit weer volgt, dat CQRM een koordenvierhoek is. [einde Opmerking] |
3.3. De punten P, Q en R zijn collineair
![]()
Natuurlijk is stelling 2 ook juist als de punten P, Q, R collineair
zijn (zie figuur 6).
| figuur 6 | 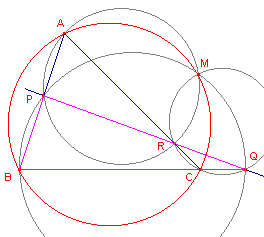 |
Bij driehoek ABC is de Miquel-configuratie (PQR, ABC) getekend. Het punt M is het punt van Miquel van deze configuratie. Beschouw nu driehoek PBQ. |
We kunnen dit ook algemeen formuleren:
Opmerking
Zie voor een ander bewijs van Stelling 4 de pagina "Draaivermenigvuldiging".
[einde Opmerking]
Klik hier ![]() voor een CabriJavapplet
van stelling 4.
voor een CabriJavapplet
van stelling 4.
| figuur 7 | 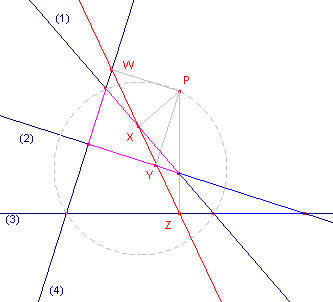 |
Zij P het gemeenschappelijk punt van de omcirkels van de driehoeken. De loodlijnen uit P op de vier lijnen hebben de snijpunten W, X, Y, Z met die lijnen. Voor
driehoek 134 is XZW de Simson-lijn van P. Deze lijn is de lijn van Simson van elk van die driehoeken. Opmerking |
[einde Toelichting]
De afbeeldingen en animaties op deze pagina zijn gemaakt met behulp van Cabri Geometry II.