We gaan uit van het punt van Lemoine van een driehoek.
Door dat punt trekken we (de) drie lijnen die antiparallel zijn met de zijden en snijden die lijnen met de zijden.
We vinden dan
Verband tussen de Brocard-punten, het Lemoine-punt en een Miquel-punt
Overzicht ][ Brocard | Lemoine | Miquel | Meetkunde
Zie ook de pagina "Brocard-driehoeken"
1. Cirkel van
Lemoine ![]()
We gaan uit van het punt van Lemoine van een driehoek.
Door dat punt trekken we (de) drie lijnen die antiparallel zijn met de zijden en snijden
die lijnen met de zijden.
We vinden dan
| Stelling 1 De snijpunten van de met de zijden antiparallelle lijnen die door het point van Lemoine gaan, met de zijden, zijn concyclisch. De cirkel heet cirkel van Lemoine (de tweede cirkel van Lemoine). |
Bewijs: zie figuur 1.
| figuur 1 | 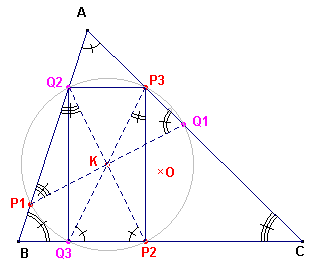 |
K is het punt van Lemoine van de driehoek. De lijnstukken P1Q1, P2Q2, P3Q3 zijn antiparallel met de zijden van de driehoek. Daaruit volgt gelijkheid van hoeken aangegeven in de figuur. Zo is �A = �P3Q3C (P3Q3 ap AB) �A = �P2Q2B (P2Q2 ap AC) Dus DKP2Q3 is gelijkbenig: KP2 = KQ3. Maar de antiparallellen worden door de symmedianen middendoor gedeeld (zie Stelling 5 op de pagina "Isogonalen"). K is dus het midden van alle lijnstukken PiQi. Dus KP2 = KQ3 = KQ2 = KP3. P2Q3Q2P3 is dus een rechthoek die een omgeschreven cirkel heeft (met middelpunt K). |
Uit de gelijkheid van de met �B en �C
overeenkomende hoeken volgt dan dat alle vanuit K getrokken lijnstukken gelijk zijn.
De zes punten liggen dus op een cirkel, die de (tweede) cirkel van Lemoine
(Emile Lemoine, 1840-1912, Frankrijk) wordt genoemd. �
Opmerking
Een algemene behandeling van de beide Lemoine-cirkels
staat op depagina "Tucker-cirkels".
De beide Lemoine-cirkels komen ook aan de orde op het Cabri-werkblad "Parallel en antiparallel".
[einde Opmerking]
2. Twee
driehoeken ![]()
De zes concyclische punten vallen uiteen in twee deelverzamelingen P1, P2,
P3 en Q1, Q2, Q3.
Hiervoor geldt
| Stelling 2 De driehoeken P1P2P3 en Q1Q2Q3 zijn congruent en beide gelijkvormig met driehoek ABC. |
Bewijs: zie figuur 2.
| figuur 2 | 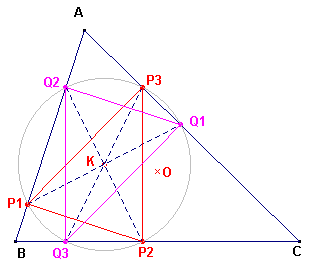 |
De punten liggen op de cirkel van Lemoine met middelpunt K (zie
Stelling 1) Passen we nu een puntspiegeling met centrum K toe op P1P2P3, dan gaat deze over in Q1Q2Q3. Dus DP1P2P3 @ DQ1Q2Q3 P1,
P2, Q2 liggen op een Thales-cirkel (middelpunt is het midden van
P2Q2). Dus �P2P1Q2 = 90�.
Dus |
3. Een
Miquel-configuratie geeft een punt van Brocard ![]()
Drie punten die elk (willekeurig) op een zijde van een driehoek liggen bepalen een
zogenoemde Miquel-configuratie. In dit geval kijken we naar de
configuratie (P1P2P3, ABC).
De stelling van Miquel zegt nu dat de Miquel-cirkels
door ��n punt gaan, het punt van Miquel van de
configuratie.
We vinden nu een bijzondere eigenschap van dat punt van Miquel :
| Stelling 3 Het Miquel-punt van de Miquel-configuratie (P1P2P3, ABC) is een punt van Brocard van driehoek P1P2P3 �n ook van driehoek ABC. |
Bewijs: zie figuur 3.
| figuur 3 | 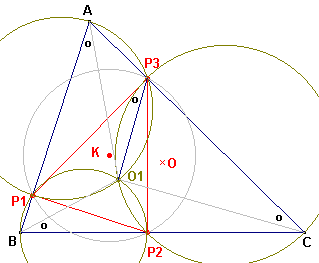 |
O1 is het punt van Miquel bij de configuratie (P1P2P3, ABC). P1P2 raakt aan de Miquel-cirkel op AB en gaat door P3; P2P3 raakt aan de Miquel-cirkel op BC en gaat door P1 P3P1 raakt aan de Miquel-cirkel op CA en gaat door P2.. Maar dit zijn juist de cirkels waarmee het punt van Brocard van driehoek P1P2P3 wordt geconstrueerd (zie Stelling 7 op de pagina "De punten van Brocard"). O1 is dus een punt van Brocard van driehoek P1P2P3. O1P3
is een "Brocard-lijnstuk"; dus �O1P3P1
= w . |
Dus ook �O1AB = w .
O1 is dus eveneens een punt van Brocard van driehoek ABC. �
Gevolg
We kunnen nu driehoek P1P2P3 onderwerpen aan een rotatie
met centrum O1 en hoek -90� (wijzerrichting).
Hierdoor komen ABC en het beeld P1'P2'P3' van P1P2P3
in homothetische ligging (zie figuur 4).
| figuur 4 | 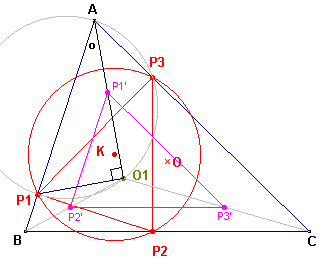 |
Hieruit volgt O1P1' / O1A = O1P1 / O1A = tan w (zie driehoek O1P1A) Dus O1P1 = O1A . tan w De gelijkvormigheidsfactor van ABC naar P1P2P3 is dus tan w . Voor de stralen van de omcirkels geldt dan evenzeer r1 = R . tan w waarin r1 en R opvolgend de straal van de cirkel van Lemoine en de straal van de omcirkel van ABC is. En ook O1K = O1O . tan w [einde Gevolg] |
4. Het tweede
punt van Brocard erbij, de cirkel van Brocard ![]()
Op dezelfde manier als hierboven, in paragraaf 3, voor O1
gedaan is, kunnen we een afleiding geven voor het tweede punt van Brocard, O2.
Zie figuur 5.
| figuur 5 | 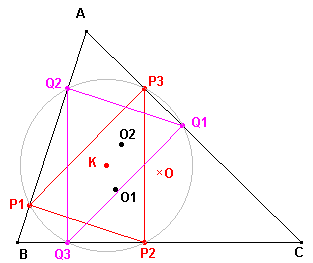 |
Voor O2 geldt dan natuurlijk ook O2K = O2O . tan w Uit het feit, dat OO1 = OO2
(dit is een eigenschap van de beide Brocard-punten; zie Stelling
8 op de pagina "Punten van Brocard"), kunnen we
dus concluderen We kunnen nu de volgende stelling (Stelling 4) met betrekking tot O, O1, O2 en K bewijzen. |
| Stelling 4 De punten O, O1, O2, K liggen op een cirkel met middellijn OK. Deze cirkel heet de cirkel van Brocard. |
Bewijs: zie figuur 6.
| figuur 6 | 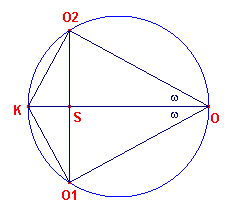 |
Zoals we gezien hebben (in het tweede deel van Stelling 3)
kunnen we de figuur in homothetische ligging plaatsen door een rotatie om O1
over een hoek van -90� (wijzrrichting). Het beeld van K ligt dan op OO1.
hierbij Dus �KO1O = 90� en dus eveneens �KO2O = 90� Uit O1K = O1O . tan w volgt dan verder, dat de beide hoeken bij O gelijk zijn aan de hoek van Brocard w . |
De punten O, O1, K, O2 zijn dus de hoekpunten van een
koordenvierhoek.
Waarmee het gestelde is aangetoond.�
Opmerking
Zie ook de pagina Brocard-driehoeken
waarop enkele andere eigenschappen van de Brocard-cirkel worden behandeld.
[einde Opmerking]
Gevolg
In driehoek OO1S is dan (zie weer figuur 6)
sin w = SO1 / OO1
zodat
SO1 = OO1 . sin w
en dan ook
SO2 = OO2 . sin w
Er is dus sprake van dezelfde factor, sin w ,
die de gelijkvormigheidsfactor is van de voetpuntsdriehoeken van de punten van Brocard
tov. driehoek ABC (zie Stelling 8.1 op de pagina "De punten van Brocard").
Deze voetpuntsdriehoeken hebben dus beide dezelfde omcirkel met middelpunt S
en straal gelijk aan R . sin w.(zie
figuur 7)
| figuur 7 | 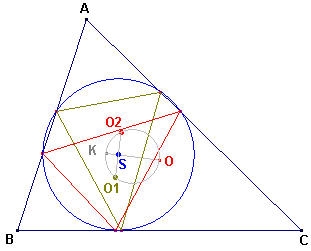 |
Opmerkingen [1] Dat de voetpuntsdriehoeken van de punten van Brocard dezelfde omcirkel hebben, blijkt ook uit het feit, dat de punten van Brocard isogonaal verwant zijn (Stelling 8.5 en 8.6 op de pagina "De punten van Brocard"); immers isogonale punten hebben dezelfde omcirkel (zie hiervoor ook Stelling 3 op de pagina "Isogonale punten"). [2] Het blijkt ook uit het feit, dat de voetpunten op de tweede cirkel van Lemoine liggen (zie de pagina "Tucker-cirkels"). [einde Opmerkingen en einde Gevolg] |