Zie ook de pagina's "Brocard-driehoeken" en "Constructie van de Brocard-hoek".
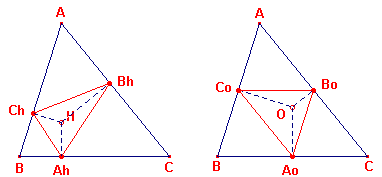
| Definitie De driehoek gevormd door de voetpunten van de loodlijnen uit een punt P op de (verlengden van de) zijden van een driehoek A1A2A3 heet voetpuntsdriehoek van P tov. de driehoek. De producten p1 = PA1 . A2A3, p2 = PA2 . A1A3, p3 = PA3 . A1A2 heten voetpuntsproducten van P. |
Bekende voetpuntsdriehoeken zijn (zie figuur 1):
| figuur 1 voetpuntsdriehoek van het hoogtepunt H en van het middelpunt O |
 |
2. Stellingen ![]()
Voor de voetpuntsproducten en -driehoeken bewijzen we de volgende
stellingen
| Stelling 1 De zijden van de voetpuntsdriehoek van P verhouden zich als de voetpuntsproducten van P. |
Bewijs: zie figuur 2.
| figuur 2 | 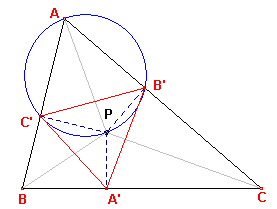 |
A'C'PB' is een koordenvierhoek; de middellijn van de omgeschreven cirkel
is AP. Nu is volgens de sinusregel: B'C' / sin A = 2RAC 'B ' = AP en in driehoek ABC geldt ook BC / sin A = 2R (R is de straal van de omgeschreven cirkel van driehoek ABC) Hieruit volgt dus B'C' = AP . BC / (2R) = p1 / (2R) Evenzo vinden we C'A' = p2 / (2R) en A'B' = p3 / (2R) |
Noemen we de zijden van driehoek A'B'C' opvolgend a', b', c', dan is
a' : b' : c' = p1 : p2
: p3 �
| Stelling 2 De vier voetpuntsdriehoeken van ��n punt uit P, A, B, C tov. de driehoek met de andere punten als hoekpunten zijn gelijkvormig. |
Bewijs: zie figuur 3.
| figuur 3 | 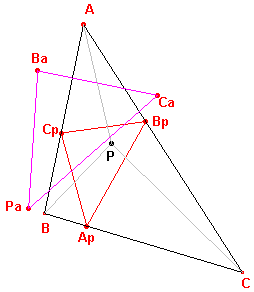 |
ApBpCp is de voetpuntsdriehoek van P
tov. ABC: PaBaCa is de voetpuntsdriehoek van A tov. PBC. Volgens stelling 1 is nu: |
| Stelling 3 Ligt P op de omgeschreven cirkel van ABC dan zijn de voetpunten van de loodlijnen op de (verlengden van de) zijden collineair. Deze collineatie-as heet de rechte van Simson (ook wel rechte van Wallace). |
Bewijs: zie figuur 4.
De voetpuntsdrehoek van P is ontaard in een rechte lijn!
| figuur 4 | 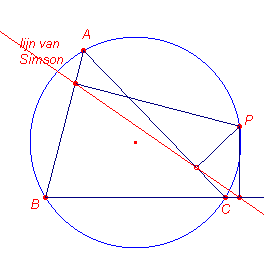 |
Volgens de stelling van Ptolemaeus is nu in
koordenvierhoek ABCP: PB . AC = PA . BC + PC . AB Dus p2 = p1 + p2 Volgens stelling 1 is a' : b' : c' = p1 : p2 : p3 Met evenredigheidsfactor k hebben we dus a' = kp1, b' = kp2, c' = kp3 Zodat voor zijden a',b',c' van "driehoek A'B'C' " geldt b' = a' + c' Dit kan alleen als A', B' en C' collineair zijn. � |
| Stelling 4 De inversen van de hoekpunten van een driehoek tov. een punt P vormen een driehoek die gelijkvormig is met de voetpuntsdriehoek van dat punt. |
Opmerking
Deze stelling wordt met behulp van het begrip antiparallel
voor rechte lijnen bewezen als Stelling 6.2 op de pagina
"Inversie".
[einde Opmerking]
Bewijs: zie figuur 5.
| figuur 5 | 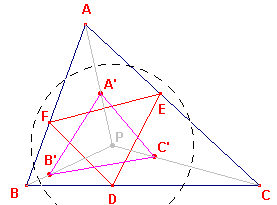 |
In deze figuur is - DEF de voetpuntsdriehoek van punt P - A'B'C' de driehoek die door inversie van de punten A,B,C tov. P ontstaan is. Nu is: EF : FD : DE = (PA.BC) : (PB.AC) : (PC.AB) (zie stelling 1) En ook vanwege de "vermenigvuldigingseigenschap" van lijnstukken bij inversie - de factor is k2/(ab) met a, b als afstanden van het inversiecentrum eindpunten A,B van het oorspronkelijke lijnstuk : A'B' = k2/(PA.PB) . AB = k2/(PA.PB.PC) . (PC.AB) A'C' = k2/(PA.PC) . AC = k2/(PA.PC.PB) . (PB.AC) B'C' = k2/(PB.PC) . BC = k2/(PB.PC.PA) . (PA.BC) |
Dus EF : FD : DE = B'C' : A'C' : A'B', waaruit het gestelde volgt (zzz). �
3. Punten van
Brocard ![]()
We noemden in de Inleiding reeds dat de voetpuntsdriehoek van het
middelpunt van ABC rechtstreeks gelijkvormig is met driehoek ABC zelf; maw.
D A'B'C' ~ D ABC.
We willen nu de punten O bepalen waarvoor
(1) D A'B'C' ~ D
BCA (het bijbehorende punt noemen we O1)
(2) D A'B'C' ~ D
CAB (het bijbehorende punt noemen we O2)
De punten O1 (het eerste punt) en O2 (het tweede punt) heten naar
hun ontdekker de punten van Brocard (Henri Brocard, 1845-1922, Frankrijk)
Bewijs: alleen voor [1].
Uit de gelijkvormigheid volgt a' : b' : c' = b : c : a
Uit stelling 1 vinden we a' : b' : c' = p1 : p2
: p3 = (q1.a) : (q2.b)
: (q3.c)
(q1.a) : (q2.b) : (q3.c)
= b : c : a
waaruit
q1 : q2 : q3
= (b/a) : (c/b) : (a/c) �
Gevolg
De beide punten van Brocard kunnen worden geconstrueerd met twee Apollonius-cirkels van driehoek ABC.
Een dergelijke constructie is echter niet zo eenvoudig uit te voeren.
Zie voor een eenvoudige constructie het gevolg van Stelling 7 (die weer
het gevolg is van Stelling 6).
Of zie de pagina "Constructie van de Brocard-hoek".
Ten behoeve van de volgende stelling gaan we uit van een constructie van het punt O1 van Brocard met behulp van twee cirkels van Apollonius (waarvan we in het bewijs geen gebruik maken).
| Stelling 6 Voor O1 als het eerste punt van Brocard van driehoek ABC geldt �O1AB = �O1BC = �O1CA. Deze hoek heet (de eerste) hoek van Brocard en wordt meestal aangegeven met de letter w. |
Bewijs: zie figuur 6.
| figuur 6 | 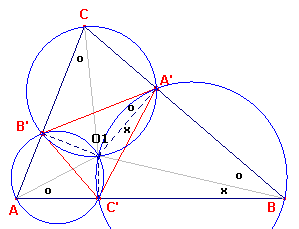 |
In deze figuur is A'B'C' de voetpuntsdriehoek bij O1.Dus: A'B'C' ~ BCA. Daaruit volgt: �A' = �B. We tekenen de omcirkels van de drie koordenvierhoeken. Nu is �O1A'C' = �O1BC' (staan op gelijke bogen van O1A'BC'). Dus: �O1BC = �O1A'B'. Maar ook �O1A'B' = �O1CB' (gelijk bogen van O1A'CB'). We vinden dus: �O1AB = �O1BC = �O1CA � |
Opmerkingen
[1]
De tweede hoek van Brocard is gelijk aan de eerste. Klik
hier voor het bewijs van deze eigenschap.
[2]
Het eerste punt van Brocard (en dus ook het tweede) wordt gevonden als een speciaal geval
van de Miquel-configuratie.
[3]
Zie ook de pagina "Constructie van de Brocard-hoek".
[einde Opmerkingen]
Een gevolg van Stelling 6 is de voor de constructie van de punten van Brocard belangrijke
| Stelling 7 De cirkel door O1 en door A en B raakt in B aan BC; de cirkel door O1 en door B en C raakt in C aan CA; de cirkel door O1 en door C en A raakt in A aan AB. |
Bewijs: zie figuur 7.
| figuur 7 | 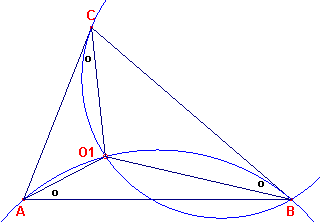 |
In de cirkel door O1, A en B staat hoek A op boog O1B.
Deze hoek is gelijk aan hoek CBO1. Deze hoek staat dus ook op die boog. Er is dus sprake van raking van de cirkel door O1, A, B in het punt B. � Gevolg |
4. Gevolgen van
de gelijkvormigheid ![]()
De gevolgen van de gelijkvormigheid van de driehoeken A'B'C' en BCA kunnen we formuleren
in de volgende twee stellingen (stelling 8 en stelling 9)
| Stelling 8 [1] De gelijkvormigheidsfactor van ABC naar C'A'B' is gelijk aan sin w. [2] Voor w geldt : cot w = cot A + cot B + cot C [3] Bij O1 en O2 behoort dezelfde hoek w. [4] OO1 = OO2 waarin O het middelpunt is van de omgeschreven cirkel van ABC. [5] O1 en O2 zijn isogonaal verwant tov. driehoek ABC. [6] De voetpuntsdriehoeken van O1 en O2 hebben dezelfde omgeschreven cirkel. |
Bewijs: zie figuur 8a.
| figuur 8a | 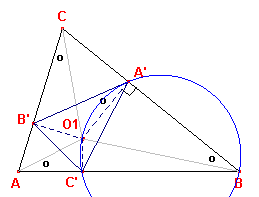 |
[1] In rechthoekige driehoek O1A'B is O1A'/O1B = sin w. Dus O1A' = O1B . sin w Op dezelfde manier: O1B' = O1C . sin w en O1C' = O1A . sin w. Driehoek A'B'C' kan dus uit BCA onstaan door draaiing om O1 gevolgd door een vermenigvuldiging met de factor sin w. � |
[2]
Uit de gelijkvormigheid O1AC'~O1BA'~O1CB' volgt
O1A' : O1B' : O1C' =
O1B : O1C : O1A = (c/b) : (a/c) :
(b/a) - zie stelling 5
Uit de driehoeken O1AC' en O1AB' (beide rechthoekig) volgt:
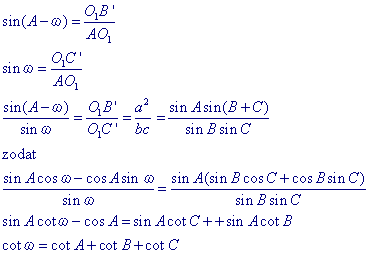
�
[3]
Een dergelijke afleiding, als in stelling 8.2, kunnen we ook geven voor
O2, zodat ook bij O2 dezelfde hoek w
hoort. �
Gevolg
De hoek van Brocard is dus voor elke driehoek eenduidig bepaald.
[einde Gevolg]
[4]
De vermenigvuldigingsfactor van ABC naar B"C"A" (de voetpuntsdriehoek bij O2)
is nu ook sin w (zie stelling 8.3 en zie stelling 8.1)
Dit geldt dus ook voor vermenigvuldiging van O tov. O1 en O2,
waaruit onmiddellijk volgt dat O1O = O2O (zie figuur 8b). �
| figuur 8b | 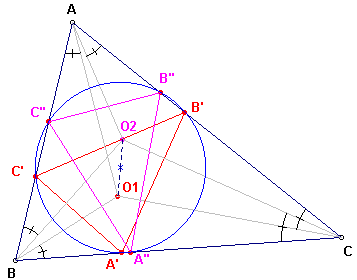 |
[5] Dat O1 en O2 isogonaal verwant zijn blijkt onmiddellijk uit eenduidig bepaalde hoek w voor O1 en O2 uit de gelijkheid van de hoeken bij A, B en C. � [6] Opmerking |
| Stelling 9a [1] De (tweede) snijpunten A1, B1, C1, van de lijnen AO1, BO1, CO1 met de omcirkel van driehoek ABC vormen een driehoek die congruent is met ABC. [2] Het punt O1 is ook punt van Brocard van driehoek A1B1C1. |
Bewijs: zie figuur 9b.
| figuur 9a | 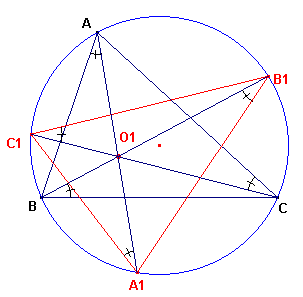 |
Uit de gelijkheid van omtrekshoeken volgt onmiddellijk, dat
driehoek A1B1C1 ~ driehoek ABC. Nu is in driehoek ABC: a / sinA = 2R (R is straal van de omcirkel). En in driehoek A1B1C1 is: a1 / sinA = 2R Dus a = a1. Waaruit de congruentie volgt. De lijnstukken A1O1, B1O1, C1O1 bepalen het punt van Brocard van driehoek A1B1C1. � |
| Stelling 9b Voor de driehoeken ABC en A1B1C1 (1e Brocard-punt O1), waarbij AA1 /\ BC = D, BB1 /\ AC = E, CC1 /\ AB = F, geldt: 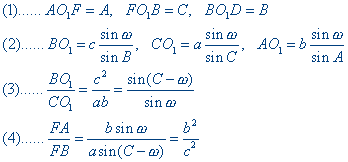 (zie figuur 9b) (zie figuur 9b) |
| figuur 9b | 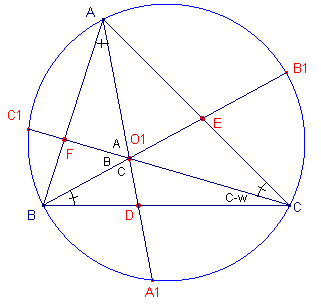 |
De hoek van Brocard geven we hieronder aan met w. (1) (2) (3) |
(4)
In driehoek BCF is (volgens de sinusregel): BF / sin(C - w) = a / sin F.
In driehoek AFC is (volgens de sinusregel): AF / sin w = b / sin F.
Zodat AF / BF = (b / a) � (sin w / sin (C - w).
Dit laatste is volgens (3) gelijk aan (b / a) � (ab / c2) = b2 / c2
�
5.
Oppervlakte ![]()
Uit Stelling 8 volgt eenvoudig
| Stelling 10 De voetvoetsdriehoeken van O1 en O2 hebben gelijke oppervlakten. |
Een ander bewijs van stelling 10, ook gevonden door Gergonne (Joseph Gergonne, 1771-1859, Frankrijk) en gepubliceerd in 1823, willen we hier niet onvermeld laten.
Bewijs: zie figuur 10.
Nota Bene
Met enige aanpassing van het onderstaande bewijs kan worden aagetoond, dat voor een
voetpuntsdriehoek van een willekeurig punt P geldt, dat de oppervlakte gelijk is aan:
��(R2 - MP2) � sin(A) � sin(B) �
sin(C)
Punten die evenver van M liggen, hebben dus voetpuntsdriehoeken met gelijke
oppervlakten!
Zie hiervoor de pagina "Oppervlakte van
voetpuntsdriehoeken".
[einde NB]
| figuur 10 | 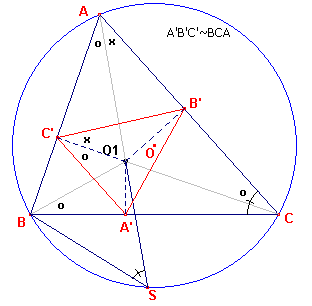 |
Zij S het tweede snijpunt van AO1 met de omcirkel (deze heeft
straal R). Uit koordenvierhoek AB'O1C' volgt: hoeh B'C'O1 = hoek B'AO1. Verder hoek B'AO1 = hoek SBC (dezelfde boog op de omcirkel) Dus hoek C' = hoek SBO1. Nu is
immers in driehoek O1BS is TS/sinSBO1 = TB/sin(S) |
Deze oppervlakte is dus alleen afhankelijk van de ligging van O1 en O (het
middelpunt van de omcirkel van ABC).
De voetpuntsdriehoeken van O1 en O2 (immers OO1 = OO2;
zie ook Stelling 8.4) hebben dus gelijke oppervlakten. �
| Stelling 11 [1] Voor w geldt: [2] Voor w geldt: w � 30� |
Bewijs:
[1]
We kunnen de stelling direct uit de definitie van de cotangens-functie en de cosinusregel
afleiden:
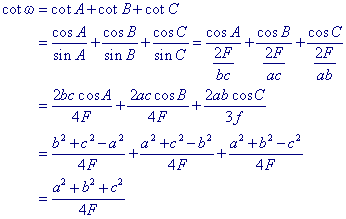
�
[2]
In elke driehoek geldt
cot
B cot C + cot C cot A + cot A cot B
= 1
Kwadratering van cot w = cot A + cot B + cot C
(zie stelling 8) geeft dan
![]()
Uit de ongelijkheid
![]()
volgt dan
cot w � �3
Dus: w � 30� �
6. Samenhang ![]()
Er bestaat een direct verband tussen de de punten van Brocard, het punt
van Lemoine en het punt van Miquel in een speciale
Miquel-configuratie.
Klik hier voor een beschrijving van dat
verband.
Op de pagina Brocard-driehoeken
worden nog enkele andere eigenschappen van de Brocard-punten behandeld.
Zie ook de pagina "Neuberg-cirkels".