De stelling van Ptolemaeus en
de sinusregel
Ptolemaeus | SIN-regel | Somformule ][ Cosinusregel | Meetkunde
Zie ook: Meetkunde-werkblad:
De Stelling van Ptolemaeus
Zie ook: Stelling van Van Schooten
1. De stelling van Ptolemaeus 
Ptolemaeus van Alexandri? (100-168) heeft naam
gemaakt met zijn planetentheorie, die hij uiteen zette in een verhandeling die bekend
staat als Almagest (een verbastering van de latere arabische titel Al magiste,
de grootste). Ook gaf hij de benadering van 377/120 voor de waarde van p.
Hij bewees tevens de stelling die nu zijn naam draagt.
Stelling
ALS ABCD is een vierhoek die is ingeschreven in een cirkel DAN de som van de producten
van lengtes van de paren overliggende zijden is gelijk aan het product van de lengtes van
de diagonalen. |
Met andere woorden: AB . CD + AD . BC
= AC . BD
| figuur 1a |
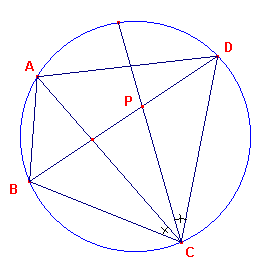 |
Eerste bewijs: (zie figuur 1a)
Kies op de diagonaal BD een punt P, zodat ?ACB = ?PCD. Omdat de hoeken BAC en BDC op dezelfde boog staan, zijn ze aan
elkaar gelijk. De driehoeken ABC en DPC zijn dus gelijkvormig, waaruit volgt, dat CD/PD =
CA/BA, of
AB . CD = AC . PD.
De hoeken BCP en ACD zijn eveneens gelijk, zodat de driehoeken BCP en ACD eveneens
gelijkvormig zijn, waaruit volgt BC/BP = AC/AD, of
BC . AD = AC . BP
Tellen we beide resultaten op, dan vinden we
| AB . CD + BC . AD |
= AC . PD + AC . BP
= AC . (BP + PD)
= AC . BD ? |
|
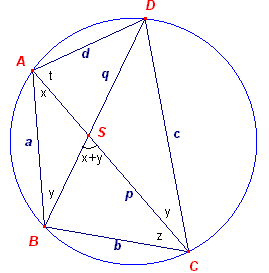
Tweede bewijs: (zie figuur 1b en figuur 1c)
In de figuren hieronder zijn de gebruikelijke aanduidelingen voor de zijden (a,b,c,d)
en de diagonalen (p,q) gebruikt.
We moeten dus aantonen dat:
ac + bd = pq
| figuur 1b |
figuur 1c |
|
 |
 |
In figuur 1b geldt dat voor alle hoeken rond het punt
S de sinus-waarden aan elkaar gelijk zijn; zodat: Opp(kvh ABCD) = ?pq sin(x + y) ......(1)
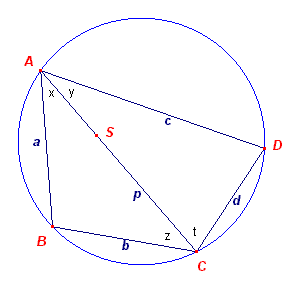
In figuur 1c hebben we driehoek ACD op een andere manier binnen de
cirkel geplaats (gespeigeld in de middelloodlijn van AC).
Nu is:
Opp(kvh ABCD) =
?ac sin(x+y) + ?bd sin(z+t) =
?(ac + bd)sin(x+y) ......(2)
Uit (1)en (2) volgt dan direct het gestelde. ? |
Opmerkingen
[1] Deze stelling kan ook worden bewezen met gebruikmaking van inversie. Klik hier voor dit bewijs.
[2] De stelling van Ptolemaeus volgt ook als een bijzonder geval uit de stelling van Casey.
[3] ? Klik hier voor een bewijs
van de cosinusregel, gebaseerd op de stelling van Ptolemaeus.
[4] ? Zie ook
het Werkblad
Meetkunde: De stelling van Ptolemaeus (het werkblad zelf is alleen beschikbaar als
PDF)
[5] ? Zie ook
de pagina 'De
Stelling van Van Schooten'.
[einde Opmerkingen]
2. De
sinusregel 
In Propositie III, 20 van de Elementen van Euclides
vinden we
Stelling
In een cirkel is een hoek aan het middelpunt het dubbele van een hoek aan den omtrek,
wanneer de hoeken denzelfden boog als de basis hebben
(vertaling Dr. E.J. Dijksterhuis) |
Meestal wordt deze stelling als volgt geformuleerd (Stelling van de omtrekshoek):
Een omtrekhoek is gelijk aan de helft van de middelpuntshoek op dezelfde boog van de
cirkel.
Klik hier voor het in de Elementen
staande bewijs van de stelling.
Met behulp van deze stelling kunnen we het bewijs van de sinusregel heel eenvoudig
leveren. Deze luidt
Sinusregel
In een driehoek geldt voor de zijden en hoeken van een die driehoek
a / sin(A) = b / sin(B) = c / sin(C) = 2R
waarbij R de straal van de omgeschreven cirkel van de driehoek is |
|
figuur 2 |
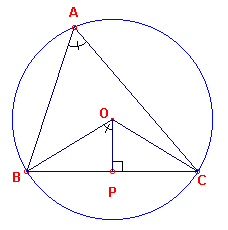 |
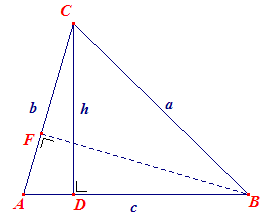
Eerste bewijs: (zie
figuur 2) Hierin is OB = R.
Dus nu geldt in driehoek BOP, dat sin(BOP) = BP / R = (BP+PC) / 2R = a / 2R = sin(A).
Of
a / sin(A) = 2R
Herhalen we deze stappen ook voor de punten B en C dan is daarmee de sinusregel dus
bewezen.
Indien ??n der hoeken van de driehoek stomp is, verloopt het bewijs op dezelfde manier. ?
Gevolg
Indien de straal van de omgeschreven cirkel gelijk is aan ?, vinden we dus een
eenvoudiger uitdrukking voor de zijden:
a = sin(A), b= sin(B), c = sin(C)
[einde gevolg]
Tweede bewijs:
In driehoek ADC hebben we: sin(A) = h / b; in driehoek BDC hebben we sin(B)
= h / a.
Hieruit volgt dan: h = b . sin(A) en h = a . sin(B), zodat
b . sin(A) = a . sin (B)
Maar dit is hetzelfde als a / sin(A) = b / sin(B).
Op dezelfde manier kunnen we in de driehoeken AFB en CFB bewijzen dat
a / sin(A) = c / sin(C), zodat inderdaada / sin(A) = b / sin(B) = c / sin(C)
? |
 |
3. Som- en
verschilformule 
De stelling van Ptolemaeus geeft ook een elegante manier om twee andere goniometrische
identiteiten te bewijzen, namelijk de zogenoemde som- en verschilformule voor
de sinus.
Deze luiden
| (1) |
sin(A + B) = sin(A)cos(B) + cos(A)sin(B) |
| (2) |
sin(A - B) = sin(A)cos(B) - cos(A)sin(B) |
Bewijs:
Beschouw een vierhoek ABDC ingeschreven in een cirkel waarvan de diameter gelijk is aan 1,
terwijl de diagonaal BD middellijn is (zie figuur 3).
Uit de definitie van de sinus en de cosinus bepalen we de lengtes van de zijden van de
vierhoek. De sinusregel geeft daarna de lengte van de andere diagonaal.
De somformule is dan niets anders dan een andere manier van schrijven van de stelling van
Ptolemaeus.
| figuur 3 |
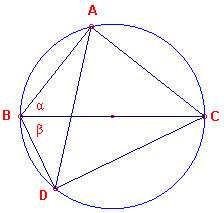 |
BC = 1
AB = cos a (in de rechthoekige driehoek ABC)
AC = sin a
BD = cos b (in de rechthoekige driehoek BDC)
DC = sin b
AD = sin (a + b) (zie
Gevolg in paragraaf 2)
|
|
Dus volgens de stelling van Ptolemaeus:
AD.BC = AC.BD +
AB.CD
of
sin(a + b)
=
sin a cos b + cos a sin b |
Ook bij het bewijs van de verschilformule (zie figuur 4) dient BC als diameter van de
cirkel.
| figuur 4 |
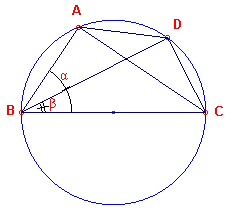 |
BC = 1
AB = cos a
AC = sin a
BD = cos b
DC = sin b
AD = sin (a - b) |
|
Dus volgens de stelling van Ptolemaeus:
AD.BC + AB.CD =
AC.BD
of
AD.BC = AC.BD -
AB.CD
of
sin(a - b)
=
sin a cos b - cos a sin b
waarmee beide formules bewezen zijn. ? |

[sinregel.htm] laatste wijziging op: 02-01-2013 (23/09/2007)






