prop III-20 | prop III-21 | Gevolg ][ Elementen | Meetkunde
| Propositie III-20 In een cirkel is een hoek aan het middelpunt het dubbele van een hoek aan den omtrek, wanneer de hoeken denzelfden boog als de basis hebben. (vertaling Dr. E.J. Dijksterhuis) |
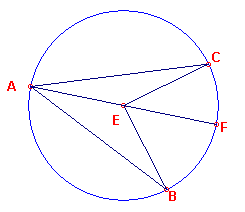
Laat ABC een cirkel zijn (zie figuur 1), laat de hoek BEC een hoek aan het middelpunt
zijn, en de hoek BAC een hoek aan de omtrek, en laten beide dezelfde boog BC als basis
hebben;
ik zeg, dat de hoek BEC het dubbele is van de hoek BAC.
| figuur 1 |  |
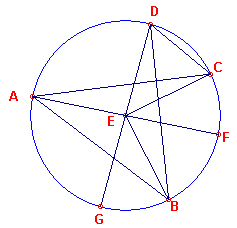
figuur 2 |  |
Is AE verbonden en verlengd naar F.
Dan, omdat EA gelijk is aan EB, is de hoek EAB ook gelijk aan de hoek EBA [I, 5];
daarom zijn de hoeken EAB, EBA [samen] het dubbele van de hoek EAB.
Maar de hoek BEF is gelijk aan de hoeken EAB, EBA [I, 32];
daarom is de hoek BEF ook het dubbele van de hoek EAB.
Om dezelfde reden is de hoek FEC ook het dubbele van de hoek EAC.
Daarom is de gehele hoek BEC het dubbele van de gehele hoek BAC.
Laat ook een andere lijn getekend zijn (zie figuur 2), en laat er een andere hoek BDC zijn; laat DE verbonden zijn en verlengd tot G.
Op dezelfde manier kunnen we bewijzen dat de hoek GEC het dubbele is van de hoek EDC,
waarvan de hoek GEB het dubbele is van de hoek EDB;
daarom is de hoek BEC die overblijft, het dubbele van de hoek BDC.
Daarom is de hoek BEC het dubbele van de hoek BAC.
Hetgeen te bewijzen was. ?
| Propositie III-21 In een cirkel zijn de hoeken in hetzelfde segment [op dezelfde koorde; dk] aan elkaar gelijk. |
Zij ABCD een cirkel, en zijn de hoeken BAD, BED hoeken in hetzelfde segment BAED [dit
is boog BCD; dk];
ik zeg dat de hoeken BAD, BED aan elkaar gelijk zijn (zie figuur 3).
| figuur 3 | 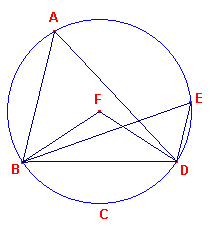 |
Want zij het middelpunt van de cirkel genomen, en zij het F; laten BF, FD
verbonden zijn. Nu is, omdat de hoek BFD ligt in het middelpunt en de hoek BAD op de omtrek, en ze hebben dezelfde omtrek [boog; dk] BCD als basis, daarom de hoek BFD het dubbele van de hoek BAD [III-20]. Om dezelfde reden is de hoek BFD het dubbele van de hoek BED; Hetgeen te bewijzen was. ? |
Gevolg
We kunnen het omgekeerde van deze stelling bewijzen door gebruikt te maken van een bewijs
uit het ongerijmde.
| Stelling (omgekeerde van Propositie
III-21) Hebben twee gelijke hoeken dezelfde basis en staan ze aan dezelfde kant van de basis, dan gaat de cirkel door de eindpunten van de basis en een hoekpunt ook door het andere hoekpunt. |
Bewijs:
| We bekijken de omgeschreven cirkel van driehoek ABC en bewijzen, dat het
punt D hierop ligt. Stel D ligt niet op de cirkel. De cirkel snijdt dan het lijnstuk BD (of het verlengde van het lijnstuk BD) in een punt E. Zij dan E verbonden met C. Dan is ?BEC = ?BAC [prop. III-20]. Dus is ?BEC = ?BDC. Maar BEC is buitenhoek van driehoek en deze is gelijk aan de som van de niet-aanliggende binnenhoeken [prop. I-16]. We hebben dus een tegenspraak. Dus ligt D ook op de cirkel. ? |
figuur 4 | 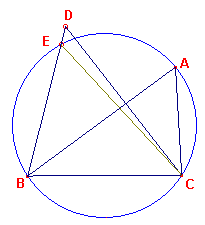 |
Opmerking
Deze stelling wordt in moderne context als volgt geformuleerd (zie ook figuur 5):
| figuur 5 | 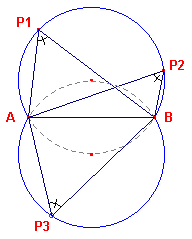 |
De verzameling van de punten waaruit een gegeven lijnstuk gezien
wordt onder een gegeven hoek, bestaat uit twee gelijke cirkelbogen, waarvan de eindpunten
samenvallen met die van het lijnstuk. De eindpunten van het lijnstuk behoren niet tot de verzameling |
? Zie ook de pagina "Middelpunts- en omtrekshoeken".
[einde Opmerking]