Apollonius-cirkel(s), isodynamische punten
Overzicht ][ Vierzijde | Meetkunde
Zie ook de pagina "Isodynamische punten"
1. Definitie
![]()
We zoeken de meetkundige plaats van alle punten P waarvan voor de afstanden van dat punt
tot twee vaste punten A en B geldt:
PA / PB = k
Als k = 1, dan geldt PA = PB. De gezochte meetkundige plaats is dan de
middelloodlijn van AB.
We veronderstellen nu k � 1.
| figuur 1a | Kiezen we nu (bijvoorbeeld) k = 2, dan kunnen we op de lijn AB (in ieder geval)twee punten P vinden waarvoor PA : PB = 2 : 1; zie de punten C en D in figuur 1a. |
Hierin is: CA : CB = 2 :1 en DA : DB = 2 :1.
Maar er zijn natuurlijk meer punten P.
We moeten het punt P z� kiezen, dat PA = 2 PB.
We kunnen de ligging van P nu onderzoeken door een cirkel te tekenen met middelpunt B en
straal �PA.
P moet nu op deze cirkel liggen (zie figuur 1b).
| figuur 1b | 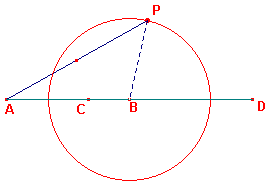 |
Immers, als P op de cirkel (P, �PA) ligt, dan is PA : PB = 2 : 1. Het bovenstaande is opgenomen in de nu volgende CabriJava-animatie. |
|�| Klik hier ![]() om met behulp van een animatie
de meetkundige plaats van de punten P te vinden.
om met behulp van een animatie
de meetkundige plaats van de punten P te vinden.
| Stelling 1 De meetkundige plaats van de punten X, waarvoor XA : XB = k : 1 (met k � 1) is een cirkel met CD als middellijn, waarbij C en D punten zijn die het lijnstuk AB in- en uitwendig verdelen in de verhouding k. Deze cirkel heet de Apollonius-cirkel bij de verhouding k. |
Bewijs:
(deel 1) Stel X is een punt van de meetkundige plaats.
|�| Klik hier ![]() om met behulp van een animatie de
cirkels van Apollonius bij verschillende verhoudingen k te bekijken.
om met behulp van een animatie de
cirkels van Apollonius bij verschillende verhoudingen k te bekijken.
(deel 2) Stel X ligt op de cirkel met middellijn CD. Te bewijzen is nu: AX : BX = k : 1.
| figuur 3 | 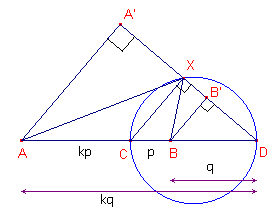 |
Zie nu figuur 3. Zijn A’, B’ de projecties van A, B op de lijn door D en X. Nu geldt: BB’ : AA’ = 1 : k. Ook is nu: B’X : XA’ = BC : CA = 1 : k. Dus BB’X ~ AA’X, zodat BX : AX = BB’ : AA’ = 1 : k. Zodat AX : BX = k : 1. � |
Opmerking
De meetkundige plaats van de punten waarvan afstanden tot twee rechte lijnen zich
verhouden als a : b, bestaat uit twee rechte lijnen.
Zie hiervoor Isogonale verwantschap.
[einde Opmerking]
2.
Constructie van de Apollonius-cirkel ![]()
Oplossing 1
Zijn C en D de punten die een lijnstuk AB in- en uitwendig verdelen in een verhouding v.
De punten A, B, C, D liggen dus harmonisch.
Wanneer we nu alleen het punt C kennen, dan kunnen we het punt D dus als vierde
harmonische bij A, B en C construeren.
De cirkel van Apollonius bij AB en verhouding v is dan de cirkel met middellijn CD.
Oplossing 2
Is de verhouding gegeven door de lengte van twee lijnstukken p en q, dan
verloopt de constructie het eenvoudigst op basis van gelijkvormigheid van driehoeken.
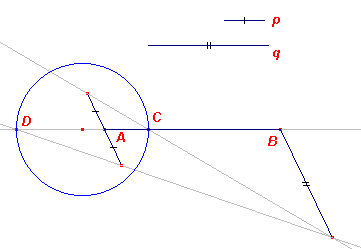 |
Teken op een lijn door A het lijnstuk p, aanweerszijden van A. Teken op
een lijn door B (evenwijdig met die door A) het lijnstuk q. De verbindingslijnen van de eindpunten (zie nevenstaande figuur) snijden de drager van het gegeven lijnstuk AB in de punten C en D. De punten C en D verdelen AB dan in- en uitwendig in stukken die zich verhouden als p : q. De cirkel met middellijn CD is dan de gevraagde Apollonius-cirkel. � Zie CabriFAQ 43 voor een macro-constructie die op deze oplossing gebaseerd is. |
3. Apollonius-cirkels van een driehoek / Isodynamische
punten ![]()
Gaan we uit van een ongelijkzijdige driehoek ABC met zijden a, b,
c.
Voor de punten X van de Apollonius-cirkel bij de verhouding b/a geldt XA : XB = b
: a.
Het punt C ligt dus op die Apollonius-cirkel, evenals de snijpunten P en Q van de binnen-
en buitenbissectrice van hoek C met de zijde AB.
Deze cirkel heet wel C-Apollonius-cirkel van driehoek ABC.
Er zijn dus drie Apollonius-cirkels bij een driehoek: AB met b/a, BC met c/b,
CA met a/c (zie figuur 4, waarin slechts twee cirkels getekend
zijn; de A- en de B-cirkel).
| Stelling 2 De drie Apollonius-cirkels van een ongelijkzijdige driehoek snijden elkaar in twee punten. |
Bewijs:
Zie figuur 4, waarin Ma en Mb de
middelpunten zijn van de Apollonius-cirkels op BC en CA.
| figuur 4 | 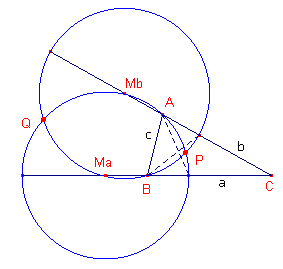 |
We ordenen de zijden van de driehoek zo, dat a > b > c. Voor het punt X op de Apollonius-cirkel van AC geldt: XA : XC = c : a. Omdat c < a, geldt dat A binnen deze cirkel ligt. Voor het punt X op de Apollonius-cirkel van BC geldt: XB : XC = c : b. Omdat c < b geldt, dat B binnen deze cirkel ligt. Beide cirkels hebben dus twee snijpunten. Stel dat P zo’n snijpunt is. Voor P geldt: PB/PC = c/b �n PA/PC = c/a. Dus PA/PB = (c/a) / (c/b) = b/a. Dus het punt P ligt ook op de Apollonius-cirkel van AB.� |
De beide gemeenschappelijke punten heten de isodynamische punten
van de driehoek.
� Zie verder de pagina "Isodynamische punten"
| Stelling 3 Als in driehoek ABC geldt dat a > b > c, en Ra, Rb, Rc zijn de stralen van de Apollonius-cirkels, dan is 1 / Rb = 1 / Ra + 1 / Rc |
Bewijs (zie figuur 5):
| figuur 5 | 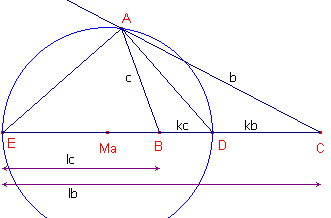 |
We drukken Ra eerst uit in de zijden van de driehoek. Voor positieve k hebben we: kc + kb = a, zodat k = a / (b + c). Dus BD = ac / (b + c) EC - EB = a = lb - lc = l (b - c) waaruit volgt l = a / (b - c). Dus EB = ac / (b - c).
Ra = �DE = abc / (b2-c2) |
Dus 1 / Ra + 1 / Rc = (b2 - c2 + a2 - b2) / abc = (a2 - c2) / abc = 1 / Rb. �
| Stelling 4 De drie middelpunten van de Apollonius-cirkels van een driehoek zijn collineair. |
Bewijs (zie figuur 6)
| figuur 6 | 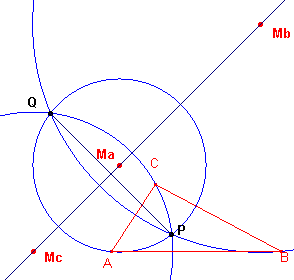 |
Ma, Mb, Mc zijn de middelpunten van de
Apollonius-cirkels van driehoek ABC. Zijn P en Q de isodynamische punten van de
driehoek. Opmerking |
| Stelling 5 De Apollonius-cirkels van een driehoek snijden de omgeschreven cirkel van die driehoek loodrecht. |
| figuur 7 | 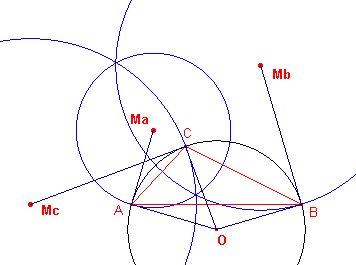 |
Bewijs: Het bewijs hiervan kan gemakkelijk geleverd worden door gebruik te maken van harmonische ligging. Klik hier voor het bewijs. � Opmerking |
| . |
| Stelling 6 De Apollonius-cirkels van een driehoek snijden elkaar twee aan twee onder hoeken van 60� . |
Bewijs:
Dit bewijs verloopt op eenvoudige wijze door gebruik te maken van harmonische ligging en
inversie.
Klik hier voor het bewijs.�
4. Andere
eigenschappen ![]()
[1]
Apollonius-cirkels spelen, zoals opgemerkt bij enkele stellingen in
paragraaf 3, ook een rol bij harmonische ligging.
Klik hier voor een bewijs van enkele van
deze eigenschappen.
[2]
� Zie ook de pagina "Isodynamische punten" voor enkele eigenschappen in samenhang
met de Lemoine-lijn.
[3]
Op die pagina wordt ook bewezen, dat de voetpuntsdriehoek van een isodynamisch punt
gelijkzijdig is (klik hier voor die stelling).