De lijn van Simson en een enveloppe
Inleiding | Stelling | Lijn | Enveloppe | Hypocyclo?de ][ Meer bijzonderheden | Meetkunde
Zie ook het Cabri-werkblad: De lijn
van Simson
Zie ook de pagina "Meer bijzonderheden van de
Simson-lijn"
Zie ook de pagina "Generalisatie van de
Simson-lijn"
Zie ook de pagina "De lijn van Simson, het
punt van Miquel en de lijn van Steiner"
Zie ook de pagina "Over de
Simson-lijn van het Steiner-punt en van het Tarry-punt"
| Lijn van Simson De voetpunten van de loodlijnen uit een punt P op de zijden van een driehoek ABC liggen alle op een lijn (Simson's lijn of ook lijn van Wallace of voetpuntsrechte van P tov. driehoek ABC) dan en slechts dan als het punt P op de omgeschreven cirkel van driehoek ABC ligt. |
Opmerking
Robert Simson (1687-1768, Schotland) zelf heeft met deze
lijn niets van doen.
Door onderzoek van J.S Mackay is in 1890 vast komen te staan, dat de bedoelde lijn nergens
in het werk van Simson voorkomt. De lijn wordt voor het eerst vermeld door Wallace (William Wallace, 1768-1843, Schotland) in 1799.
[einde Opmerking]
| Enveloppe (Fr. enveloppe = wat tot inwikkelen dient). Omhullende, ook
wel omhulde. De kromme (het oppervlak), waaraan alle exemplaren van een enkelvoudig
oneindig stelsel krommen (oppervlakken) raken, verdient evenzeer den naam omhulde als dien
van omhullende. (Uit: Dr. E.J. Dijksterhuis, Vreemde woorden in de wiskunde, P. Noordhoff N.V., 1948, Groningen) |
1. De
"stelling van Simson" ![]()
Voordat we een en ander met betrekking tot de enveloppe van de lijnen van Simson bij een
bepaalde driehoek zullen opmerken, kijken we eerst naar de (hier zogenaamde) stelling
van Simson (naar analogie van de Simson-lijn vernoemen we deze stelling - Stelling 1 -
naar Simson).
Bij het bewijs daarvan maken we gebruik van meetkundige transformaties (een ?nog? weinig
aan bod komend facet van het huidige meetkunde-onderwijs). We bewijzen:
Bewijs: We kijken eerst naar de som (het na elkaar uitvoeren)
van twee spiegelingen in twee snijdende lijnen. We zullen aantonen (zie
figuur 1):
De som van twee spiegelingen in twee elkaar in O snijdende lijnen die een hoek met
elkaar maken is een rotatie met O als centrum over een hoek 2.
| figuur 1 | 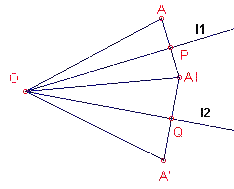 |
Opmerking Met de functie h(X) of h(AXB) geven we in hetgeen volgt de hoekgrootte aan van hoek X. [einde Opmerking] Zij A een willekeurig punt van het vlak, zij A1 het beeld van A in l1 en A' het beeld van A1 in l2. P en Q zijn opvolgend de snijpunten van de spiegelassen en de verbindingslijnstukken AA1 en A1A'. Nu is onmiddellijk duidelijk, dat OA = OA' en dat h(AOA') = 2.h(POQ). |
Voor het bewijs van onderdeel (a) van de stelling van Simson kijken we naar figuur 2.
| figuur 2 | 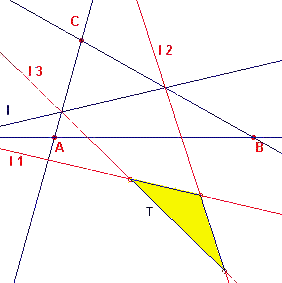 |
De lijn l2 wordt verkregen uit l1 als
som van twee spiegelingen in opvolgend AB en BC. Hierdoor is de hoek tussen l1
en l2 gelijk aan tweemaal de hoek tussen AB en BC. De hoeken van
driehoek T worden dus alleen bepaald door de hoeken van driehoek ABC en hangen dus niet af
van de positie van de lijn l. Zou driehoek ABC rechthoekig zijn, dan zijn twee van de lijnen l1, l2 en l3 evenwijdig. Daardoor vormen ze geen driehoek T. |
We gaan nu verder met het bewijs van onderdeel (b), dat belangrijk is voor ons doel.
Voordat we dat doen kijken we eerst naar figuur 3.
Bewijs van onderdeel (b)
Neem aan, dat de lijn l geroteerd is om een willekeurig punt M in het vlak.
De zijden van de driehoek T gaan dan altijd door de punten M1, M2 en M3 die symmetrisch liggen met M ten opzichte van de zijden van driehoek ABC; met andere woorden, driehoek T verandert zo, dat hij gelijkvormig blijft met zichzelf., terwijl de zijden steeds door drie vaste punten gaan (zie figuur 4, waarin het rotatiepunt M op de lijn l zelf gelegen is).
In dit geval hebben elk tweetal posities van de driehoek T eenzelfde rotatiecentrum O.
| figuur 4 | 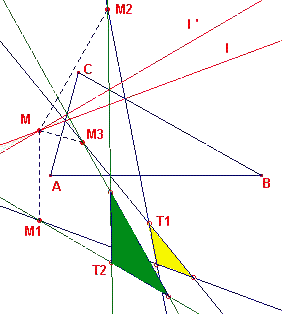 |
Gaat l1 door dat punt O (dat wil zeggen, dat l
door het punt O' gaat dat symmetrisch ligt met O ten opzichte van de zijde AB), dan (en
alleen dan) gaat driehoek T over in een punt, waardoor ook de lijnen l2
en l3 door O gaan. We zien dus dat, in het algemeen, onder de lijnen die door een gegeven punt M gaan er slechts ??n lijn l is waarvoor l1, l2 en l3 concurrent zijn; als er twee van deze lijnen zouden zijn, zou dat betekenen, dat alle lijnen door M die eigenschap zouden hebben. Zijn nu M en N twee punten en zijn l en l' de lijnen door die punten waarvoor l1, l2, l3 en l1', l2', l3' door ??n punt gaan. Als H nu het snijpunt is van l en l', dan geldt dat voor elke lijn door H de overeenkomstige lijnen l1, l2, l3 door ??n punt gaan. |
(De lijnen l en l' kunnen niet evenwijdig zijn, omdat, als l1, l2, l3 door een punt O gaan, en als l // l', dan de lijnen l1', l2', l3' evenwijdig zouden zijn aan de overeenkomstige lijnen l1, l2, l3 en op een afstand van O zouden liggen die gelijk is aan de afstand tussen l en l'; daarom kunnen ze niet door ??n punt gaan).
Als l door H gaat, dan gaan l1 en l2 door de
punten H1 en H2 die symmetrisch liggen met H ten opzichte van de
zijden van driehoek ABC. Omdat daarbij de hoek tussen l1 en l2
een vaste grootte geeft (zie het bewijs van onderdeel a), zien we dat
het snijpunt P van de lijnen l1 en l2 een cirkel S
beschrijft (de meetkundige plaats van de punten waaronder het lijnstuk H1H2
gezien wordt onder die vaste hoek).
We hebben dus het bestaan van een punt H aangetoond waarvoor geldt dat voor elke lijn door
dat punt H de lijnen l1, l2, l3 door
een vast punt gaan.
Er kunnen geen twee punten G en H bestaan, omdat er anders door elk punt M twee lijnen MG
en MH zouden zijn waarbij voor elk van beide de overeenkomstige lijnen l1,
l2, l3 door ??n punt zouden gaan.
Om in te zien, dat H het snijpunt is van de hoogtelijnen van driehoek ABC en S de
omgeschreven cirkel daarvan is, is het voldoende op te merken, dat de lijnen l1,
l2, l3 overeenkomend met de hoogtelijnen van ABC
elkaar snijden in de hoekpunten van de driehoek.
Voor de volledigheid van de stelling van Simson geven we ook het bewijs van onderdeel (c), hoewel een en ander voor de rest van dit betoog irrelevant is.
| figuur 5 | 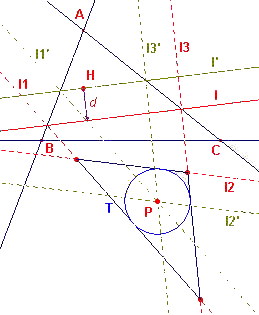 |
Zie figuur 5. Zij l een willekeurige lijn en zij l' een lijn die ermee evenwijdig is en gaat door het punt H. De lijnen l1', l2', l3' gaan dan door een punt P. De afstand van dit punt P tot de lijnen l1, l2, l3 is gelijk aan de afstand van l en l' (zie bewijs van onderdeel b). Deze afstand is dus ook gelijk aan de afstand d van H tot l. De straal van de ingeschreven cirkel van driehoek T is dus gelijk aan d. Omdat alle driehoeken T gelijkvormig zijn, volgt hieruit, dat de oppervlakte van driehoek T slechts afhangt van de afstand van H tot l. Bij een vaste oppervlakte van T liggen alle lijnen l dus op een vaste afstand van H. Ze raken dus aan een cirkel met middelpunt H. ? |
| figuur 6 | 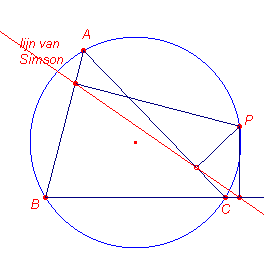 |
Gaan we uit van de omgeschreven cirkel van een driehoek, en kiezen we op
die cirkel een punt P, dan kunnen we uit dat punt loodlijnen neerlaten op de zijden van de
driehoek (of op het verlengde daarvan). De voetpunten van deze loodlijnen liggen dan op
een rechte lijn, de lijn van Simson (zoals gezegd, ook wel lijn van Wallace
(William Wallace, 1768-1843) of voetpuntsrechte genoemd).
Klik hier We bewijzen nu de volgende stelling |
| . |
| Stelling 2 De voetpunten van de loodlijnen neergelaten vanuit een punt P op de zijden van een driehoek ABC liggen op een lijn desda het punt P ligt op de omgeschreven cirkel van ABC. |
We geven van deze stelling drie bewijzen:
1. een bewijs gebaseerd op de "Stelling van Simson" (zie Stelling 1)
2. een bewijs dat gebruik maakt van de configuratie van Miquel
3. een bewijs dat een direct gevolg is van de Stelling van Ptolemaeus
4. een bewijs gebaseerd op koordenvierhoeken
P moet dus liggen op de omgeschreven cirkel van ABC en l' moet door het hoogtepunt van ABC gaan (zie de stelling van Simson, onderdeel b).
Er bestaat een verband tussen de lijn van Simson en de negenpuntscirkel zoals we in stelling 3 zullen zien.
Tweede bewijs: (zie figuur 8)
| figuur 8 | 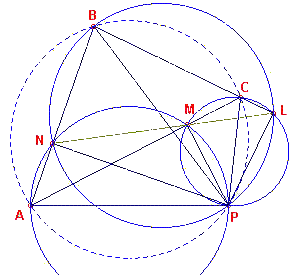 |
Zijn N, L, M opvolgend de voetpunten op de zijden AB, BC, AC. We
beschouwen nu de "driehoek" NLM. Nu is h(PMA) = h(PNA) = 90o; N, M , A en P liggen dus op de Thales-cirkel met middellijn AP. Dezelfde overwegingen leiden tot: P ligt op cirkel BNL en P ligt op cirkel CLM. P is nu het punt van Miquel van de configuratie (LMN, ABC). P is dus het rotatiecentrum van alle driehoeken L'M'N' die gelijkvormig zijn met LMN en waarvan de hoekpunten liggen op de zijden BC, CA en AB van driehoek ABC. |
Verder is
(1) h(APB) = h(APN) + h(NPB) = h(AMN) + h(NLB)
omdat APN en AMN alsmede NPB en NLB omtrekshoeken zijn op dezelfde boog van een cirkel.
Maar nu is
h(AMN) = h(MCN) + h(MNC) en h(NLB) = h(NCB) - h(LNC)
zodat
(2)
h(AMN) + h(NLB) = ( h(MCN) + h(NCB) ) + ( h(MNC) - h(LNC) ) = h(MCB) + h(MNL)
Vergelijken we nu vergelijking (2) met vergelijking (1) dan vinden we
h(APB) = h(MCB) + h(MNL)
Omdat P op de omgeschreven cirkel van ABC ligt is h(APB) = h(ACB) (omtrekshoeken
op dezelfde boog). Dus h(MNL) = 0.
Maar dit betekent, dat M, N en L collineair zijn. ?
Derde bewijs:
Voor dit bewijs wordt gebruik gemaakt van de gelijkvormigheid van voetpuntsdriehoeken en de stelling van
Ptolemaeus.
Klik hier voor dit bewijs.
| figuur 8(e) | .gif) |
In de figuur hiernaast zijn U, V, W de projecties van een punt P van de
omcirkel van driehoek ABC op de zijden. De vierhoeken PVCU en PUWB zijn dan koordenvierhoeken. In PUWB is: h(BUW) = h(BPW) = u In driehoek PVC is h(C) = h(B), zodat h(CPV) = u. In PVCU is h(CPV) = h(CUV) = u Daarmee is: h(CUV) = h(BUW). En dus liggen de punten U, V en W op dezelfde rechte lijn (overstaande hoeken). ? |
Zoals reeds is opgemerkt, bestaat er een verband tussen de lijn van Simson en de
negenpuntscirkel (cirkel van Feuerbach).
We bewijzen
| Stelling 3 Het snijpunt van de lijn van Simson en het lijnstuk PH ligt op de negenpuntscirkel. |
Bewijs: (zie figuur 9)
| figuur 9 | 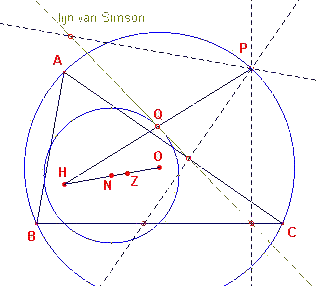 |
Een en ander volgt eigenlijk direct uit het eerste bewijs van de vorige
stelling. Daarin wordt de lijn l met de factor 2 vermenigvuldigd met als beeld de
lijn l' die dan door H gaat (zie figuur 7). Zij nu Q het midden van PH. Vermenigvuldigen we nu het punt P met H als centrum en factor ?, dan is het onmiddellijk duidelijk, dat het midden van PH op l ligt. Maar omdat de omgeschreven cirkel bij diezelfde vermenigvuldiging overgaat in de negenpuntscirkel, ligt Q dus ook op de negenpuntscirkel. ? |
Zie ook de pagina "Meer bijzonderheden van de Simson-lijn"
3. Over de
enveloppe van lijnen van Simson ![]()
Wanneer het punt P verplaatst wordt over de omgeschreven cirkel van driehoek ABC wijzigt
uiteraard ook de positie van de lijn van Simson.
| figuur 10 | 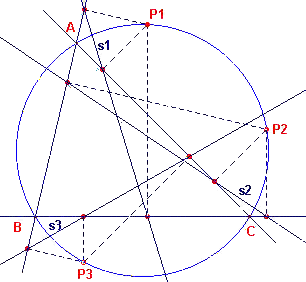 |
In figuur 10 is een drietal van deze lijnen (s1, s2,
s3) getekend. Wat er nu precies gebeurt als het punt P de omgeschreven cirkel doorloopt is uit deze figuur nog niet duidelijk. In hetgeen volgt zal echter blijken dat de lijnen een bijzondere kromme lijn insluiten. Om meer inzicht te krijgen wat er gebeurt als een punt een cirkel doorloopt waarbij de positie van een lijn afhankelijk is van de positie van dat punt, bekijken we eerst de volgende eenvoudige constructie (zie figuur 11). |
| figuur 11 | 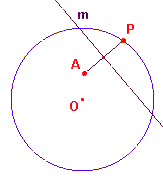 |
figuur 12 | 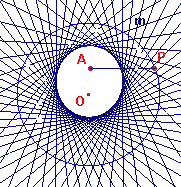 |
Binnen een cirkel met middelpunt O kiezen we een vast punt A. Het variabele punt P ligt op de cirkel. m is de middelloodlijn van het lijnstuk AP. We tekenen nu een groot aantal lijnen m bij verschillende posities van het punt P op de cirkel (zie figuur 12). Uit deze figuur blijkt nu, dat de lijnen m een figuur omsluiten.
| figuur 13 | 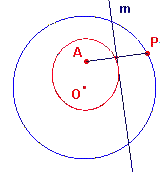 |
Alle lijnen m raken aan een kromme lijn; in dit geval is die
kromme lijn een ellips met de punten A en O als brandpunten (zie figuur 13). Een kromme lijn die op deze manier ontstaat, heet enveloppe van de lijn m (omhullende, of wellicht beter omhulde; zie ook de definitie van Dijksterhuis aan het begin van dit artikel). In figuur 13 is de ellips dus de omhulde van m (met betrekking tot P en de cirkel met middelpunt O). |
Iets dergelijks zal ook gebeuren met de lijn van Simson, als P de omgeschreven cirkel
van de driehoek doorloopt (zie figuur 14 en figuur 15).
In figuur 14 hebben we een aantal posities van de lijn van Simson getekend. In figuur 15
staat alleen de omhulde. De vorm daarvan is alleen afhankelijk van de vorm van de
driehoek.
We zien dat de vorm van de omhulde nogal gecompliceerd is. In figuur 15 is ook te zien,
dat de zijden van de driehoek aan de omhulde van de lijnen van Simson raken.
| figuur 14 | 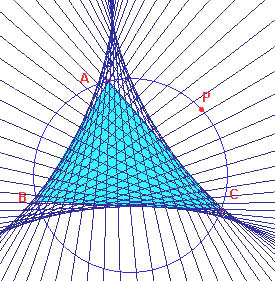 |
figuur 15 | 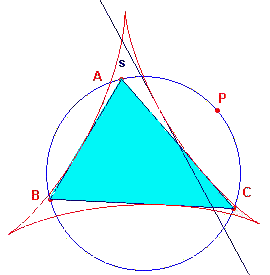 |
Klik hier ![]() voor een animatie van de raaklijnen aan de enveloppe (als in figuur 14).
voor een animatie van de raaklijnen aan de enveloppe (als in figuur 14).
4. Over de
hypocyclo?de ![]()
In hetgeen volgt zullen we aantonen, dat de vorm van de omhulde van de lijnen van Simson
bij een bepaalde driehoek een zogenoemde hypocyclo?de is.
| Hypocycloide (zie cycloide). Wanneer een cirkel over een anderen cirkel
rolt, terwijl hij dezen inwendig (vd. upo) raakt, beschrijft
ieder punt van zijn vlak een kromme, die gewone, verkorte of verlengde hypocycloide heet,
al naar gelang het punt op, binnen of buiten den rollenden cirkel ligt. Men noemt
tegenwoordig in den regel de gewonen hypocycloide zonder meer hypocycloide en vat de
andere twee samen onder den naam hypotrochoide (< Gr. trocVoV
= wiel). Wanneer echter de straal van den rollende cirkel groter is dan die van den
vasten, spreekt men wel van pericycloide, opv. -trochoide (zie trochoide). Uit: (Dr. E.J. Dijksterhuis, Vreemde woorden in de wiskunde, P. Noordhoff N.V., 1948, Groningen) |
We laten allereerst zien hoe een hypocyclo?de ontstaat als meetkundige plaats van een
punt op een cirkel die binnen een vaste cirkel rolt (zie figuur 16).
In figuur 16 is C de vaste cirkel. De cirkel C1 rolt aan
de binnenkant van deze cirkel, via het "rolpunt".A. We bekijken nu de
meetkundige plaats van het punt P dat op de omtrek van C1 ligt. Het rollen van
de cirkel C1 over C geschiedt "zonder wrijving". Dit betekent, dat
vanuit de startpositie X (van het punt A en het punt P) de lengte van boog XA (op C)
gelijk is aan de lengte van boog AP (op C1). In figuur 16
is bij een aantal posities van het punt A (na meer dan ??n omwenteling) de bijbehorende
positie van het punt P weergegeven.
| figuur 16 | 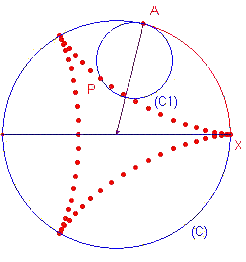 |
figuur 17 | 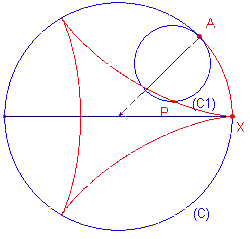 |
Klik hier ![]() voor een animatie van de hypocycloide als in figuur 16.
voor een animatie van de hypocycloide als in figuur 16.
In figuur 17 staat de gewone hypocyclo?de getekend (het
punt P ligt op de rollende cirkel). De verhouding van de stralen van de cirkels C1
en C is in dit geval 1/3. Daardoor is het aantal keerpunten gelijk aan 3.
Wanneer we figuur 15 met figuur 17 vergelijken,
dan zien we een duidelijke overeenkomst. Het vermoeden dat er in figuur 15 (bij de omhulde
van de lijnen van Simson) sprake is van een hypocyclo?de ligt voor de hand. Dit vermoeden
wordt wellicht nog sterker, als we de omhulde van de Simson-lijnen construeren als de
driehoek gelijkzijdig (zie figuur 18).
| . |
Bewijs: De lijn s is de raaklijn aan de hypocyclo?de
in het punt M. Dus PM staat loodrecht op s. De lijn s snijdt daardoor de cirkel ook
in het tegenpunt Q van O.
Zijn nu K en K' de snijpunten van s met de lijn NA en de lijn door het punt N1
evenwijdig met NA.
Het punt H is de project van Q op de lijn OA.
Zij nu h(PNA) = j.
Wegen de gelijkheid van de bogen AP en IM is dan h(PN1M) = 3j.
En dus is h(PQM) = 3j / 2 (mod p),
waaruit volgt , dat h(KQN) = j/2 (mod p),
immers PQM is buitenhoek van driehoek KQN.
Als gevolg hiervan hebben we
(1) QH / HK = tan(j/2).
(2) En dus is QH = sin(j), immers NQ = 1 (= 1/3 van NP).
Uit (1) en (2) volgt dan weer HK = QH / tan(j/2) = sin(j) / tan(j/2).
Omdat sin(j) = 2sin(j/2)cos(j/2) vinden we dan
HK = 2cos2(j/2).
We beschouwen nu de vermenigvuldiging met factor 2/3 en ten opzichte van N. Hierdoor gaat
ABC over in driehoek A'B'C.
| figuur 19 | 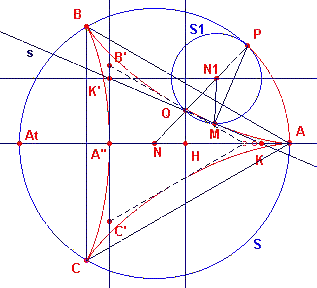 |
Zij nu verder A" het snijpunt van NA met de A'B'. Het punt A"
is het beeld van het tegenpunt At van A op de omgeschreven cirkel. Dus NA' = 1. Dan is A"H = A"N + NH = 1 + cos(j) = 2 cos2(j/2). H is dus het midden van het lijnstuk KA". Omdat Q het midden is van KK', ligt K' dus op B'C'. Dus K' is de loodrechte projectie van N1 op B'C' of anders gezegd, K' is het voetpunt van de loodlijn uit N1 op B'C'. |
Op dezelfde manier (vervanging van A door B of C, en j door j + 2p/3 of j -
2p/3) kunnen we aantonen, dat de voetpunten van de loodlijnen
uit N1 op de beide andere zijden van driehoek A'B'C' eveneens op s
liggen.
Uit de vermenigvuldiging met 2/3 met centrum O blijkt verder, dat N1 gelegen is
op de omgeschreven cirkel van driehoek A'B'C. s is dus de lijn van Simson van N1
bij driehoek A'B'C'. ?
Gevolg
| figuur 20 | 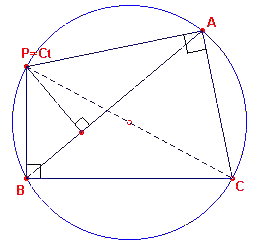 |
Dat de zijden van de driehoek aan de omhulde raken, wordt veroorzaakt
door een bijzondere ligging van het punt P op de omgeschreven cirkel van de driehoek (zie
figuur 20). Als P namelijk samenvalt met het tegenpunt van een van de hoekpunten van de driehoek (in figuur 20 is P = Ct), dan is de vierhoek APBC een koordenvierhoek waarvan hoek A en hoek B recht zijn. De voetpunten van de hoogtelijnen uit P op de zijden BC en CA vallen dan samen met opvolgend B en A. De zijde AB is in dit geval dus de lijn van Simson behorend bij P. En zo'n lijn raakt immers aan de omhulde. |
? Zie verder de
pagina "Meer bijzonderheden van de Simson-lijn"
? Zie ook de pagina
"Generalisatie van de Simson-lijn"
? Zie ook de pagina
"Over de Siimson-lijn van het Steiner-punt en
van het Tarry-punt"
De figuren op deze pagina zijn gemaakt met behulp van Cabri Geometry II.
[simson.htm] laatste wijziging op: 29-12-2008