We gaan uit van een driehoek ABC waarvan de omgeschreven cirkel middelpunt O heeft. We bekijken daarbij de "bovenste stukken" van de hoogtelijnen van de driehoek; dit zijn de lijnstukken AH, BH en CH (zie figuur 1).
Over de cirkel van Feuerbach en de lijn van Euler
Negenpuntsirkel | Euler-lijn | Simson-lijn | Meer collineaties | Stelling van Feuerbach ][ DK & meetkunde
Zie ook: Cabri-werkblad / Negenpuntscirkel
Opmerking
Op deze pagina wordt de notatie h(XYZ) gebruikt voor de hoek bepaald door de punten X, Y
en Z met Y als hoekpunt.
[einde Opmerking]
1.
Negenpuntscirkel - de cirkel van Feuerbach ![]()
We gaan uit van een driehoek ABC waarvan de omgeschreven cirkel middelpunt O heeft. We
bekijken daarbij de "bovenste stukken" van de hoogtelijnen van de driehoek; dit
zijn de lijnstukken AH, BH en CH (zie figuur 1).
| figuur 1 | 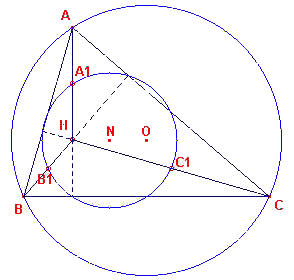 |
De middens van deze lijnstukken noemen we opvolgende A1, B1
en C1. Uiteraard liggen deze punten op een cirkel. De ligging van het
middelpunt N van deze is echter bijzonder: N is het midden van het lijnstuk HO. We kunnen dit eenvoudig aantonen. We bekijken de vermenigvuldiging ten opzichte van H met factor ?. Hierdoor gaan de punten A, B, C over in A1, B1, C1. Het middelpunt O van de omgeschreven cirkel gaat daardoor over in N, waarbij HN = ?HO. Opmerking |
Deze cirkel, die de cirkel van Feuerbach (Karl Feuerbach, 1800-1834), of ook wel negenpuntscirkel
heet; en soms ook wel cirkel van Euler, heeft aan aantal
bijzondere eigenschappen.
De tweede naam doet al iets vermoeden: er liggen namelijk negen bijzondere punten op deze
cirkel.
Klik hier ![]() voor een animatie
van de cirkel van Feuerbach en de later te behandelen lijn van Euler.
voor een animatie
van de cirkel van Feuerbach en de later te behandelen lijn van Euler.
| figuur 2 | 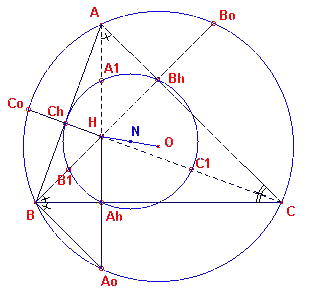 |
We kijken (zie figuur 2) naar de voetpunten Ah, Bh
en Ch van de hoogtelijnen van de driehoek (deze vormen de zogenoemde
voetpuntsdriehoek van driehoek ABC). We zullen aantonen, dat ook de voetpunten van de
hoogtelijnen op de negenpuntscirkel liggen. De rechthoekige driehoeken AAhC en BBhC hebben hoek C gemeenschappelijk. Hieruit volgt dus dat h(AhAC) = h(BhBC) We verlengen nu de hoogtelijn uit A tot deze de omgeschreven cirkel in Ao snijdt. Nu geldt ook h(AoAC) = h(CBAo), omdat beide omtrekshoeken op dezelfde boog AoC van de omgeschreven cirkel staan. Dus: h(AhBAo) = h(AhBH). Omdat BAh loodrecht staat op AoH geldt dus HAh = AhAo. We kunnen op dezelfde manier bewijzen, dat HBh = BhBo en HCh = ChCo. Bij de vermenigvuldiging ten opzichte van H met factor ? gaan nu de punten Ao, Bo, Co van de omgeschreven cirkel over in de punten Ah, Bh, Ch van de negenpuntscirkel. |
Vervolgens kijken we (zie figuur 3) naar de middens van de zijden Am, Bm, Cm van de driehoek. We zullen ook van deze punten aantonen dat ze op de negenpuntscirkel gelegen zijn.
| figuur 3 | 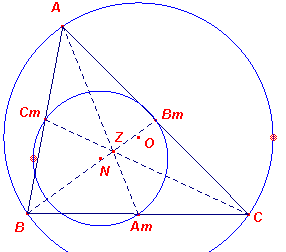 |
Ook nu maken we gebruik van een vermenigvuldiging, namelijk met centrum
Z, het zwaartepunt van de driehoek, maar dit keer met een factor -?. Zoals bekend geldt
voor de stukken waarin de zwaartelijnen door het punt Z wordt verdeeld: AZ : ZAm = BZ : ZBm = CZ : ZCm = 2 : 1. Door de laatst genoemde vermenigvuldiging gaan de punten A, B, C van de omgeschreven cirkel dus over in de punten Am, Bm, Cm van de negenpuntscirkel. En inderdaad op de negenpuntscirkel liggen negen bijzondere
punten van driehoek ABC. |
We hebben dus bewezen:
| Stelling 1 De middens van de zijden, de voetpunten van de hoogtelijnen en de middens van de "bovenste stukken" van de hoogtelijnen van een driehoek liggen op een cirkel. |
Opmerkingen
[1]
Voor een (gedeeltelijke) generalisatie van het bovenstaande zie de pagina "Oppervlakte van voetpuntsdriehoeken".
[2]
Klik hier voor een (eenvoudig) bewijs dat gebaseerd
is op gelijkvormigheid en de macht van een punt tov. een cirkel.
[einde Opmerking]
2.
Euler-lijn ![]()
We zullen nu nog aantonen dat ook het punt H collineair is met Z en O.
De lijn door de punten H. N, Z en O heet de lijn van Euler (naar Leonard Euler, 1707-1783, Zwitserland).
Klik op ![]() voor een animatie
van de lijn van Euler.
voor een animatie
van de lijn van Euler.
We bewijzen dus:
| Stelling 2 Het zwaartepunt Z, het middelpunt O van de omgeschreven cirkel en het hoogtepunt H van driehoek ABC zijn collineair, waarbij HZ : ZO = 2 : 1. |
We geven twee bewijzen voor deze stelling.
1e bewijs:
(zie figuur 4a). We gaan uit van een vermenigvuldiging ten opzichte van Z met factor -?.
Bij die vermenigvuldiging gaat driehoek ABC over in driehoek AmBmCm.
Het hoogtepunt H en de bijbehorende hoogtelijnen van ABC gaan dan over in het hoogtepunt
H' en hoogtelijnen van AmBmCm. Hierdoor zijn H, Z en H'
dus collineair.
| figuur 4a | 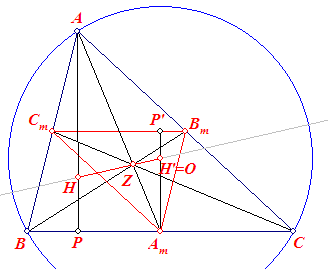 |
In figuur 4a hebben we ??n van de hoogtelijnen getekend, AP en zijn
beeld AmP'. Nu staat dus AmP' loodrecht op BmCm.
Omdat BmCm // BC, staat AmP' dus eveneens loodrecht op BC. AmP', een hoogtelijn van driehoek AmBmCm, is dus tevens middelloodlijn van driehoek ABC. En dit geldt ook voor de beide andere hoogtelijnen. Het hoogtepunt H' van driehoek AmBmCm valt dus samen met het middelpunt O van de omgeschreven cirkel van driehoek ABC. Omdat H' = O zijn dus H, Z en O collineair. ? Opmerking |
2e bewijs: (zie figuur 4b).
| figuur 4b | 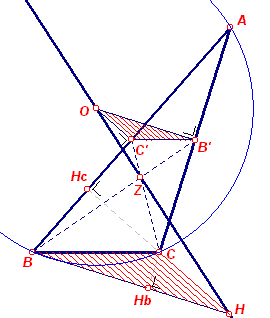 |
B' en C' zijn de middens van AB en AC. O is het middelpunt van de
omcirkel. Nu is OB' _|_ AC en OC' _|_ AB. Maar ook voor de hoogtelijnen BH en CH geldt: BH _|_ AC en CH _|_ AB. Zodat BH // OB' en CH // OC'. Verder is ook B'C' // BC (middenparallel). De driehoeken OB'C' en HBC zijn dus gelijkstandig (homothetisch). Verbindingslijnen van overeenkomstige hoekpunten zijn dus concurrent. BB' en CC' zijn zwaartelijnen van ABC die snijden in Z. Dus ook OH gaat door Z, of anders O, Z, H zijn collineair. De vermenigvuldigingsfactor is -?, zodat OZ : ZH = 1 : 2 ? |
Verwijzingen
Er zijn verschillende verbanden tussen bijzondere punten van een driehoek.
Zie hiervoor bijvoorbeeld de pagina "Fuhrmann-cirkel"
en het Cabri-werkblad "Over Spieker en Nagel".
3. De
negenpuntscirkel en de lijn van Simson ![]()
Eigenschappen van punten die op de omgeschreven cirkel van een
driehoek liggen, worden door de gelijkvormigheid van deze cirkel met de negenpuntscirkel
dus overgedragen op die laatste cirkel.
| figuur 5 | 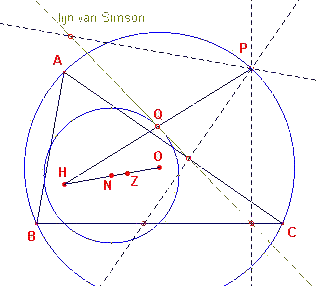 |
Uit de vermenigvuldiging met centrum H en factor -?, die uit de
omgeschreven cirkel de negenpuntscirkel laat ontstaan, volgt nu eenvoudig, dat het midden
Q van het lijnstuk HP waarbij P op de omgeschreven cirkel ligt, steeds op de
negenpuntscirkel ligt (zie figuur 5). Deze eigenschap is weliswaar niet zo erg interessant, maar hij brengt in ieder geval de lijn van Simson en de negenpuntscirkel enigszins met elkaar in verband. (De lijn van Simson is de collineatie-as van de voetpunten van de loodlijnen neergelaten vanuit een punt op de omgeschreven cirkel op de zijden van een driehoek). Merk op, dat het punt Q eveneens op de lijn van Simson ligt! |
Klik hier ![]() voor
een animatie van het punt P in samenhang met de lijn van Simson.
voor
een animatie van het punt P in samenhang met de lijn van Simson.
Klik hier voor een uitvoeriger behandeling van
de Simson-lijn.
4. Meer
collineaties ![]()
Klik hier voor enkele andere
collineaties, waarvan het bewijs min of meer op dezelfde manier verloopt als het bovenstaande.
Figuur 6 staat op een achterliggende pagina.
5. De
stelling van Feuerbach ![]()
De resultaten uit de laatste paragraaf (zie de pagina "Collineaties") kunnen we gebruiken om onderstaande
curieuze stelling te bewijzen.
| Stelling 3 (stelling van Feuerbach) De negenpuntscirkel van een driehoek raakt aan de ingeschreven cirkel (en aan de aangeschreven cirkels) van die driehoek. |
Bewijs: We tonen hieronder alleen de raking van de
negenpuntscirkel en de ingeschreven cirkel aan (zie figuur 7).
Voor het bewijs van de stelling voor raking aan de aangeschreven cirkels: zie
Opmerkingen.
| figuur 7 | 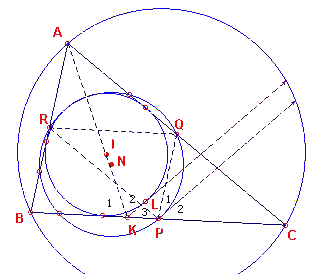 |
Het bewijs valt uiteen in drie stukken. (1) We tonen eerst aan, dat de raaklijnen een punt aan de negenpuntscirkel en in een punt aan de ingeschreven cirkel evenwijdig zijn. (2) We tonen aan dat er tussen de lijnstukken die door die punten worden bepaald, een vaste verhouding bestaat. (3) We tonen met behulp van de resultaten van 1 en 2 aan, dat er sprake is van raking. De bedoelde punten zijn (zie figuur 7) het midden P van de zijde BC (op de negenpuntscirkel) en het snijpunt K van de bissectrice van hoek A en de zijde BC. |
(1)
Zij L het raakpunt van de tweede raaklijn uit K aan de ingeschreven cirkel . Nu is
h(K1) = ? h(A) + h(C) (K1 is buitenhoek van driehoek
AKC)
h(K12) = h(A) +2h(C) (AL is bissectrice van hoek K12), en dus
h(K3) = 180o - h(A) - 2h(C) = 180o - h(A) - h(C)
- h(C) = h(B) - h(C).
Vanwege de raaklijn in P aan de negenpuntscirkel hebben we:
h(P12) = h(B), immers BA en PQ zijn evenwijdig.
h(P1) = ? bg(PQ) (omtrekshoek)
h(R1) = h(C) (overstaande hoeken in parallellogram PCQR)
h(R1) = ? bg(PQ) (omtrekshoek), zodat
h(P2) = h(B) - h(C), waaruit de evenwijdigheid van de beide
raaklijnen volgt.
| figuur 8 |  |
(2) (zie figuur 8) Bekend is GB = GI en GBK GAB.(hoeken zijn gelijk). Daaruit volgt dan GB2 = GK . GA = GI 2. Door projectie op BC blijft deze verhouding intact, zodat PI12 = PK . PD. Deze verhouding zullen we gebruiken in de beschouwing van figuur 9. (3) (zie nu figuur 9) Hierin hebben we voor de duidelijkheid een iets andere stand van driehoek ABC gekozen. |
PI1 raakt aan de ingeschreven cirkel; KL eveneens. PL snijdt de ingeschreven
cirkel voor de tweede keer in een punt S. We zullen aantonen, dat S het inwendig
raakpunt is van beide cirkels; dus dat S ook op de negenpuntscirkel ligt..
Nu geldt PI12 = PL . PS
Uit (2) vinden we nu PL . PS = PK . PD. Hieruit volgt dat de punten L, S, K, D op een
cirkel liggen (deze cirkel staat niet in de figuur). Uit de eigenschap van de
koordenvierhoek LSKD volgt dan:
h(S1) = h(K3)
Verder weten we uit (1), dat h(K3)=h(P2)
Wegens h(P2)=h(P3)=? bg(PFD) (dit is een boog van de
negenpuntscirkel) volgt dan
h(S1) = ? bg(PFD).
Dus ligt het punt S ook op de negenpuntscirkel. De ingeschreven cirkel en de
negenpuntscirkel hebben dus het punt S gemeenschappelijk.
| figuur 9 | 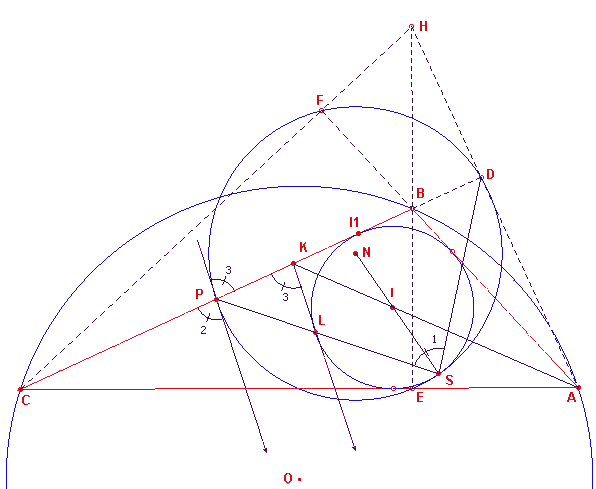 |
We moeten nu nog aantonen dat in het punt S inderdaad sprake is van raking. De
raaklijnen in L (op de ingeschreven cirkel) en P (op de negenpuntscirkel) zijn evenwijdig.
Die in S (een punt op beide cirkels) zijn dus ook evenwijdig.
Dus het punt S is raakpunt van de negenpuntscirkel en de ingeschreven cirkel. ?
Opmerkingen
[1a]
Door gebruik te maken van de theorie der inversie.kan de
stelling van Feuerbach iets eenvoudiger dan bovenstaand (en dan ook voor raking van de
aangeschreven cirkels) worden bewezen.
Klik hier voor het bewijs met inversie.
[1b]
Een bewijs, anders dan dat via de hierboven staande link, staat in het artikel "De
stelling van Feuerbach, een bewijs met inversie" (PDF-bestand, ca. 13 Kb).
Klik hier
om dat bestand te downloaden.
[2]
De omgekeerde Stelling van Casey heeft de stellling van Feuerbach eveneens tot gevolg.
Klik hier voor het bewijs.
[3]
De Stelling van Feuerbach kan ook met complexe getallen worden bewezen.
Klik hier voor dit bewijs.
[4]
Het bewijs kan ook worden gebaseerd op de voetpuntcirkels van een punt en daarmee
samenhangende isogonale verwantschap.
Klik hier voor het daarop gebaseerde bewijs.
[5]
Zie ook het artikel
D. Klingens: Draaistrekking en negenpuntscirkel. In: Euclides 81(7), mei
2006. Download (PDF-bestand, ca. 200
Kb)
[einde Opmerkingen]
De figuren op deze pagina zijn gemaakt met behulp van Cabri Geometry II.
![]()
[feuerbach.htm] (14-08-2000) laatste
wijziging op: 25-02-2008