| figuur 1 | 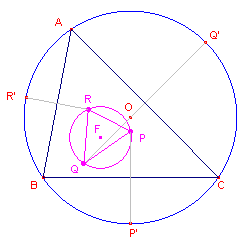 |
Deze cirkel wordt als volgt gedefinieerd (zie figuur 1):
|
Overzicht ][ Punt van Nagel | Over Spieker en Nagel | Meetkunde
1. Inleiding
Een bijzondere cirkel bij een driehoek (vergelijkbaar met de cirkel van Feuerbach
of Negenpuntscirkel) is de Fuhrmann-cirkel, genoemd
naar de Duitse wiskundige Wilhelm Fuhrmann (1833-1904).
| figuur 1 |  |
Deze cirkel wordt als volgt gedefinieerd (zie figuur 1):
|
Driehoek PQR heet Fuhrmann-driehoek (Fuhrmann zelf noemde deze driehoek Spiegeldreieck).
De cirkel door P, Q, R (de omcirkel van driehoek PQR dus) heet Fuhrmann-cirkel
(hieronder met F-cirkel) van driehoek ABC.
Het middelpunt F van deze cirkel heet het Fuhrmann-punt van driehoek ABC.
2. Eigenschappen van de Fuhrman-cirkel
| figuur 2 | 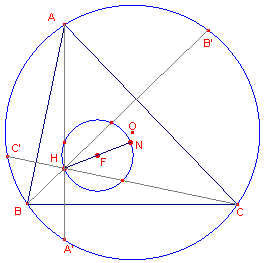 |
De eigenschappen van de Fuhrmann-cirkel staan in de volgende stelling en zijn ge�llustreerd in bovenstaande figuur (figuur 2).
Stelling
|
3. Bewijzen van
de eigenschappen
[0]
Allereerst bewijzen we de volgende
| Hulpstelling HP staat loodrecht op AP' (en ook HQ loodrecht op BQ', HR loodrecht op CR'). |
| . |
| figuur 3 | 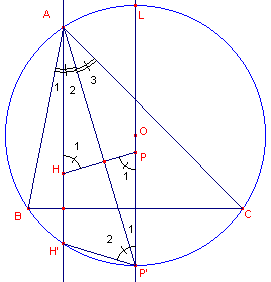 |
Bewijs: Volgens een bekend eigenschap (*) ligt het spiegelbeeld van het punt H in elk van de zijden van een driehoek op de omcirkel (zie H en H' in bovenstaande figuur). Uit de spiegeling in BC volgt dan, dat hoek HPP' = hoek H'P'P, zodat wegens de evenwijdigheid van AH' en OP' geldt: hoek H1 + hoek A2 = hoek P12 + hoek A2 = � bg H'BAL + � bg H'P' = � bg PH'BAL = 90� .� (*) |
Bewijs van [1], [2] en [3]
We maken hierbij gebruik van een eigenschap van het punt van Nagel (klik hier voor een behandeling van het punt van Nagel in
verband met Transversalen).
Voor het punt van Nagel van een driehoek (N) geldt namelijk:
het incentrum van een driehoek valt samen met het punt van Nagel van de
centrumdriehoek van die driehoek
(klik hier voor een behandeling van het bewijs van die
eigenschap - op een Cabri-werkblad).
We construeren daarom een driehoek UVW waarvan ABC de centrumdriehoek is (zie figuur 4).
| figuur 4 | 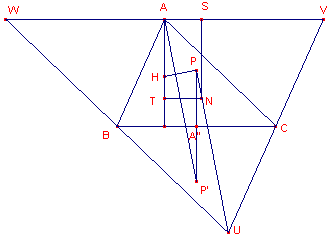 |
Het punt N is dus incentrum van driehoek UVW, zodat de lijn UN bissectrice is van hoek
U in driehoek UVW.
Verder is ABUC een parallellogram, waarvan A" het midden is van BC (op basis van de
definitie van P').
Uit de puntspiegeling s met centrum A" volgt, dat het beeld van PU (we weten nu nog
niet of N daarop ligt), en dat is P'A, ermee evenwijdig is. Dus P'A // PU.
Uit het feit, dat P' het midden is van boog BC volgt, dat P'A de bissectrice is van hoek A
in driehoek ABC.
De benen van BAP' zijn evenwijdig met de benen van PUC: BAP' = PUC.
De benen van CAP' zijn evenwijdig met de benen van BUP: CAP' = BUP.
Zodat ook UP bissectrice is van hoek U. Maar dat is de lijn UN ook.
De punten P, N en U zijn dus collineair.
Uit de hulpstelling volgt nu, dat hoek HPN = 90�
.
De punten H, P en N liggen dus op een cirkel met middellijn HN.
Op dezelfde manier kunnen we bewijzen, dat ook de punten Q en R op deze cirkel liggen.
De cirkel is dus de F-cirkel van driehoek ABC, waarvan we nu weten, dat HN een middellijn
is.
Het Fuhrmann-punt van driehoek ABC is het midden F van HN. �
Bewijs van [4]
Kijken we nu nog eens naar bovenstaande figuur (figuur 4).
Het voetpunt van N op VW is het punt S.
Omdat N het middelpunt van de incirkel is van driehoek UVW is dus NS gelijk aan de straal
van die incirkel. Wegens het feit dat ABC centrumdriehoek is van UVW is de straal van de
incirkel van UVW 2 maal de straal van de incirkel (grootte is r) van ABC. Zodat
NS = 2r.
Het voetpunt van M op AH zij nu het punt T. T ligt ook op de F-cirkel van driehoek ABC,
immers hoek HTM = 90� .
T is dus het tweede snijpunt van de hoogtelijn uit A met de F-cirkel.
AT = NS = 2r. �
| figuur 5 | 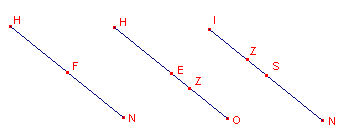 |
Door de Fuhrmann-cirkel (middelpunt F, FH = FN) wordt een verband gelegd tussen het hoogtepunt H en het punt van Nagel N.
Andere verbanden. Op enkele andere pagina's
van deze website worden andere verbanden tussen cirkels en bijzondere punten bij
een driehoek behandeld.
[1]
Door de negenpuntscirkel (middelpunt E, EH = EO) wordt een verband gelegd
tussen H (hoogtepunt), Z (zwaartepunt) en O (middelpunt omcirkel).
Klik hier voor een behandeling van de
negenpuntscirkel.
[2]
Door de Spieker-cirkel (middelpunt S, SI = SN) wordt een verband gelegd
tussen I (incentrum), Z (zwaartepunt) en N (het punt van Nagel).
Klik hier voor een behandeling van de
Spieker-cirkel en het punt van Nagel (Cabri-werkblad).
[3]
Klik hier voor de pagina over
"Transversalen", waarop het punt van Nagel eveneens wordt behandeld.
[4]
Het Furhmann-punt is het punt X355
in de Kimberling-codering van bijzondere punten van de
driehoek.
5. Download
De op deze pagina gebruikte figuren zijn in ��n bestand via deze
website te downloaden.
De figuren worden geladen met het programma Cabri
Geometry II (Windows-versie). In het bestand zijn ook enkele
Cabri-macro's en andere figuren opgenomen.
Klik hier om het downloaden te beginnen [ZIP-formaat, 9Kb].
Van deze pagina is in een iets gewijzigde vorm ook een PDF-versie
beschikbaar.
![]() fuhr.pdf [41Kb]
fuhr.pdf [41Kb]