Transversalen: de stelling van Ceva en van Menelaos
Overzicht ][ Volledige vierzijde en dubbelverhouding | DK & Meetkunde
1. Transversalen ![]()
Zie figuur 1.
Voor willekeurige punten P1 en P2 op een lijn t door het
hoekpunt van hoek S vinden we bij beschouwing van de afstand van zo'n punt tot de benen
van de hoek
P1Q1 : P1R1 = P2Q2
: P2R2
| figuur 1 | 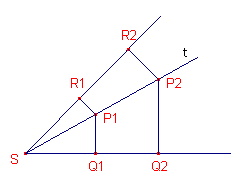 |
De lijn t is dus de verzameling van de punten die een vaste
verhouding v hebben tot de benen van de hoek, mits t binnen de hoek S
ligt. Een dergelijke lijn t heet hoektransversaal (in een driehoek ook wel ceviaan genoemd). |
2. Concurrente hoektransversalen in een driehoek (cevianen) ![]()
Zie figuur 2.
| figuur 2 | 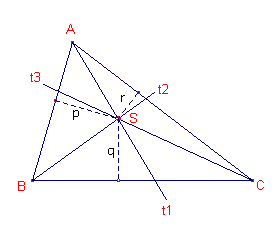 |
Voor de (punten op de) lijn t1 geldt de verhouding v1;
voor de lijn t2 geldt de verhouding v2 ; voor de
lijn t3 geldt de verhouding v3. Voor het snijpunt S van t2 en t3 geldt dus voor de afstanden, opvolgend p, q, r, tot de zijden van de driehoek p : q = v2 : 1 q : r = v3 : 1 Zodat p : q : r = v2v3 : v3 : 1 Gaat nu de ceviaan t1 ook door het punt S, dan is, r : p = v1 : 1 zodat v2v3 : 1 = 1 : v1 |
Gevolg: v1v2v3 = 1 �
3. Stelling van
Ceva ![]()
We kunnen een ceviaan ook kenmerken door de verhouding u1 van de
oppervlakte-delen waarin de driehoek door de ceviaan verdeeld wordt.
Zodat, nog steeds ervan uitgaande dat de drie cevianen door ��n punt gaan, immers dan
is v1v2v3 = 1,
u1u2u3 = 1 �
In deze vorm is de eigenschap bekend als de "beperkte" stelling van
Ceva (Giovanni Ceva, 1647-1734, Itali�; geformuleerd in
1678).
| figuur 4 | 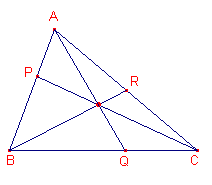 |
We kunnen dus bij concurrente cevianen schrijven (zie figuur 4), volgens (1) hierboven : PA/PB . QB/QC . RC/RA = 1 Het bovenstaande geldt alleen als de cevianen de zijden van de driehoek inwendig snijden. |
We kunnen echter generaliseren door gebruik te maken van een afspraak van M�bius (August Ferdinand M�bius, 1790-1868, Duitsland; geformuleerd in 1827).
| figuur 5 | 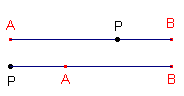 |
| Definitie Voor P op het lijnstuk AB geldt (ABP) = - PA/PB (zie figuur 5) Voor P op een verlengde van het lijnstuk AB geldt (ABP) = PA/PB Het getal (ABP) heet deelverhouding. |
De "algemene" stelling van Ceva luidt dan, met gebruik making van deze definitie:
| Stelling van Ceva Voor drie door ��n punt gaande hoektransversalen van driehoek ABC die de (verlengden van de) zijden in P,Q,R snijden geldt (ABP)(BCQ)(CAR) = -1 (noodzakelijk en voldoende) |
� Klik hier voor een iets ander bewijs van het eerste deel van de Stelling van Ceva.
4. Bijzondere
hoektransversalen ![]()
Overzicht
4.1. Bissectrices
4.2. Zwaartelijnen
4.3. Hoogtelijnen
4.4. Stelling van Pythagoras
4.5. Punt van Gergonne ![]()
4.6. Punt van Nagel ![]()
4.1. Bissectrices ![]()
Voor de bissectrices van een driehoek geldt (zie paragraaf 2):
v1 = 1, v2 = 1, v3 = 1
Nu is: v1v2v3 = 1, zodat volgens de
"beperkte" stelling van Ceva de bissectrices concurrent zijn. �
Zie ook Opmerking 2.
We kunnen een en ander nog eens nader toelichten met de bissectricestelling:
| Stelling Een bissectrice van een driehoek deelt de overstaande zijde in stukken die zich verhouden als de zijden die de hoek insluiten. |
Bewijs: (zie figuur 6)
| figuur 6 | 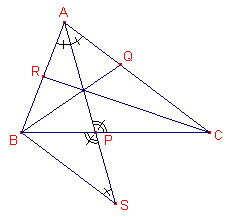 |
Maak BS (met S op de bissectrice van A) gelijk aan AB. Nu is: APC ~ SPB, waaruit volgt: CP : BP = CA : BS = CA : BA = b : c Voor de deelverhoudingen op de zijden vinden we (ABR)(BCP)(CAQ) = (-b/a).(-c/b).(-a/c) = -1 � |
Opmerkingen
[1] Zie de pagina "Stelling van Stewart" voor
de lengtes van de bissectrices.
[2] Zie de pagina "Incirkel"
voor een ander bewijs voor de concurrentie van de bissectrices.
[einde Opmerkingen]
4.2. Zwaartelijnen ![]()
Elke deelverhoudingen op de zijden zijn gelijk aan -1, met als product -1
Dus de zwaartelijnen zijn concurrent. �
Opmerkingen
[1] Zie paragraaf 7.1 voor de deelverhouding op de
zwaartelijnen zelf.
[2] Zie ook de pagina "Concurrentie van
zwaartelijnen" voor enkele andere bewijzen"
[3] Zie de pagina "Stelling van Stewart"
voor de lengte van de zwaartelijnen.
[einde Opmerkingen]
4.3. Hoogtelijnen ![]()
4.3.1. Met goniometrie (zie figuur 7a):
4.3.2. Met antiparallellen (zie figuur 7b):
Op dezelfde manier als hierboven vinden we nu
BP : BR = c : a en CP : CQ = b :
a
Zodat
| (BCP)(CAQ)(ABR) | = - PB/PC . QC/QA .
RA/RB = (wisselen van de noemers) = - PB/ RB . QC/CP . RA/QA = - c/a . a/b . b/c = -1 |
De hoogtelijnen zijn dus concurrent. �
4.3.3. Volgens Gudermann (Christoph Gudermann, 1798 - 1852, Duitsland; geformuleerd in 1835):
| figuur 7c | 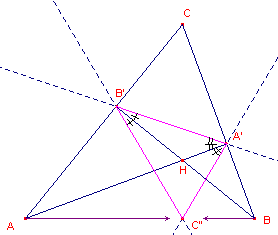 |
Zijn AA' en BB' hoogtelijnen van
driehoek ABC die elkaar snijden in het punt H (zie figuur 7c). |
(*)
Ook het concurrent zijn van ��n binnenbissectrice en twee buitenbissectrices van een
driehoek kan worden bewezen met de stelling van Ceva. �
4.3.4. Met koordenvierhoeken (zie figuur 7d)
4.4. Stelling van Pythagoras ![]()
Bij het bewijs van de stelling van Pythagoras (in boek
I, propositie 47) van de Elementen van Euclides is gebruik
gemaakt van de lijnen AE, BF en CD.
Deze lijnen zijn concurrent in het punt S (zie figuur 8).
Opmerkingen
[1]
Heron van Alexandri� (10-75, Egypte) heeft (naar het schijnt)
als eerste een bewijs van deze eigenschap gegeven.
Klik hier voor Heron's bewijs.
[2]
Zie ook de pagina "Figuur van Vecten",
Stelling 2 - Tussenresultaat
[einde Opmerkingen]
| figuur 9 | 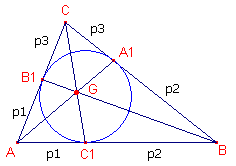 |
We gaan hierbij uit van de hoektransversalen naar de raakpunten van de
ingeschreven cirkel van de driehoek. Nu is |
Klik hier ![]() voor een animatie van bovenstaande eigenschap.
voor een animatie van bovenstaande eigenschap.
Opmerkingen
[1]
Deze eigenschap is op te vatten als een bijzonder geval van de Stelling
van Brianchon:
De verbindingslijnen van overstaande hoekpunten van een raaklijnenzeshoek (aan een
kegelsnede; in dit geval een cirkel) zijn concurrent.
De punten A1, B1 en C1 zijn in dit geval
"ontaarde" hoekpunten van zo'n zeshoek.
[2]
Klik hier voor een iets uitvoeriger
behandeling van het punt van Gergonne.
[3]
Zie ook de pagina "Barycentrische
co�rdinaten"
[einde Opmerkingen]
| figuur 10 | 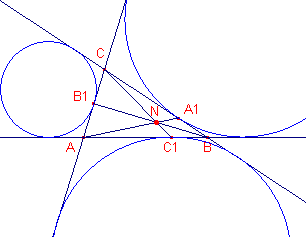 |
Hierbij nemen we de hoektransversalen naar de raakpunten van de
aangeschreven cirkels aan de zijden van de driehoek. Zoals gebruikelijk schrijven we: 2s = a + b + c. Nu is AC1 = s - b, BC1 = s - a, BA1 = s - b CA1 = s - b, CB1 = s - a, AB1 = s - c zodat (ABC1)(BCA1)CAB1) = = - (s - b)/(s - a) . (s - c)/(s - b) . (s - a)/(s - c) = -1. Het gemeenschappelijk punt van de hoektransversalen is nu N, het punt van Nagel (Christian Heinrich von Nagel, 1803-1882, Duitsland). |
Klik hier ![]() voor een animatie van bovenstaande eigenschap.
voor een animatie van bovenstaande eigenschap.
Verwijzingen
Klik hier voor Cabri-werkblad
"Over Spieker en Nagel" waarin enkele andere eigenschappen van
het punt van Nagel worden behandeld.
Klik hier voor de pagina "Fuhrmann-cirkel"
waarin het verband wordt behandeld tussen het punt van Nagel, het
hoogtepunt van een driehoek en de Fuhrmann-cirkel.
Klik hier voor de pagina
"Barycentrische co�rdinaten".
Opmerking
De eigenschappen van de raaklijnstukken kunnen we afleiden uit de volgende figuur (zie
figuur 11).
| figuur 11 | 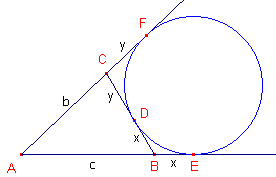 |
AE + EF = c + x + b + y = c + b + a = 2s AE = EF, zodat AE = s. Dus: BE = s - c en CF = s - b |
[einde Opmerking]
| figuur 12 | 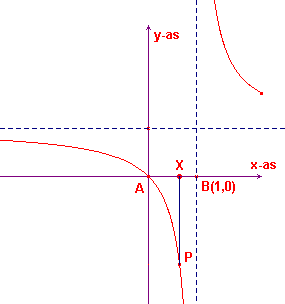 |
Kiezen we een variabel punt X(x, 0) op de lijn door de punten
A(0, 0) en B(1, 0) dan kunnen we de grafiek van de deelverhouding (ABX)
beschouwen. Nu is Hieruit volgt direct dat de deelverhouding niet gedefinieerd is voor X = B (x = 1). De grafiek heeft een horizontale asymptoot met vergelijking y = 1. |
Daarom volgt de
| Definitie ALS (ABP) = 1 DAN P heet oneigenlijk punt van de lijn door A en B. |
| Definitie Een transversaal van een driehoek is een lijn die elke zijde van een driehoek (of het verlengde ervan) snijdt in een niet-hoekpunt. |
De lijn l snijdt BC, CA en AB opvolgend in P, Q , R (zie figuur 13).
| figuur 13 | 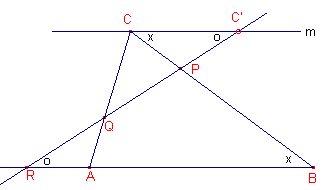 |
Met het lijnstuk CC’ (met C’ op l en CC’//AB)
vinden we BPR ~ CPC’, zodat BR : CC’ = PB : PC en RAQ ~ C’CQ, zodat AR : CC’ = AQ : CQ Nu is (ABR)(BCP)(CAQ) = = RA/RB . (BCP)(CAQ) = AQ/BP . PC/CQ . (- PB/PC) . (-QC/QA) = 1 � |
Deze eigenschap staat bekend als de stelling van Menelaos (Menelaos van Alexandri�, 70 - 130, Egypte)
| Omgekeerde stelling van Menelaos ALS (ABP)(BCQ)(CAR) = 1 DAN P, Q en R zijn collinear. |
Bewijs: (zie figuur 14).LET OP: namen van de snijpunten op de transversaal verschillen in figuur 13 en 14.
| figuur 14 | 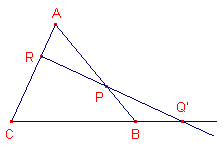 |
Stel PR snijdt CB in een punt Q’. Volgens de stelling van Menelaos is dan (ABP)(BCQ’)(CAR) = 1 Dus, samen met het gegeven, volgt dan (BCQ) = (BCQ’). En daaruit volgt dan Q’ = Q. � |
Het bovenstaande is gebaseerd op de volgende
| Stelling Voor elk re�el getal k (� 1) is er is precies ��n punt P van AB met (ABP) = k. |
Bewijs:
Zij (ABP) = k. Dan is PA : PB = k : 1
Met PA + AB = PB hebben we dan kPB - PB = - AB = BA; zodat
PB = BA / (k - 1)
Hierdoor is het punt P dus uniek bepaald. �
Opmerking
Van deze eigenschap is stilzwijgend gebruik gemaakt in de toepassingen op de bissectrices,
hoogtelijnen, ... hierboven.
[einde Opmerking]
7. Toepassingen
van de stelling van Menelaos ![]()
Overzicht
7.1. Deelverhouding bij zwaartelijnen
7.2. Drie gelijkvormigheidspunten
7.3. Stelling van d'Alembert
7.4. De Stelling van Desargues
7.5..De Stelling van Pascal voor
cirkels
7.1. Deelverhouding bij zwaartelijnen ![]()
| Stelling De zwaartelijnen van een driehoek verdelen elkaar in stukken die zich verhouden als 2:1. |
Eerste Bewijs (zie figuur 15a):
| figuur 15a | 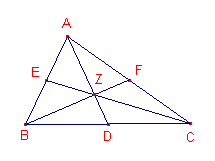 |
Beschouw de driehoek BCE met transversaal AD. Nu is: (BCD)(CEZ)(EBA) =
1. Dus ZC = 2 . ZE � |
Tweede bewijs - wat traditioneler (zie figuur 15b)
| figuur 15b | 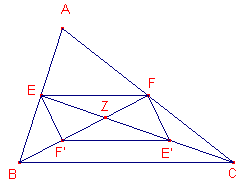 |
Zijn E' en F' de middens van CE en BF, dan is F'E'FE een parallellogram
(twee keer toepassing van de stelling van de middenparallel), zodat ZF = ZF' en daaruit volgt dan dat BZ : ZF = 2 : 1 � Opmerking |
| . |
| 7.2. Drie gelijkvormigheidspunten |
| Stelling Zijn G12, G23, G31 homothetie�n (vastgelegd als in figuur 16), dan zijn de drie gelijkvormigheidspunten collineair. |
Bewijs (zie figuur 16):
| figuur 16 | 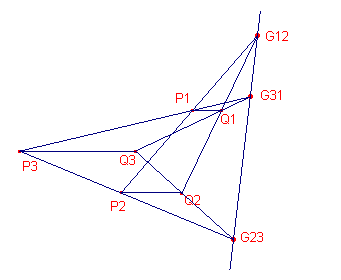 |
De centra van de homothetie�n (vermenigvuligingen tov. een punt) zijn
opvolgend (eveneens aangegeven met) G12, G23 en G31 . (P1P2G12)
= a1/a2 Het product hiervan is nu gelijk aan 1. |
7.3 Stelling van d'Alembert ![]()
Deze eigenschap genoemd in paragraaf 7.2 maar dan geformuleerd voor
cirkels, wordt wel genoemd naar Jean d'Alembert, 1717-1783, Frankrijk.
| Stelling van d'Alembert Van drie cirkels liggen de uitwendige gelijkvormigheidspunten op een rechte lijn. Twee inwendige (negatieve) gelijkvormigheidspunten en het daarbij niet behorende derde uitwendige (positieve) gelijkvormigheidspunt zijn eveneens collineair. |
Opmerking
Deze stelling wordt in de literatuur ook wel aangegeven als de Cirkelstelling
van Monge (naar Gaspard
Monge, 1746-1818, Frankrijk).
De eigenschap werd namelijk door d'Alembert aan Monge voorgelegd en ook, als eerste, door
Monge bewezen, via een 3-dimensionale voorstelling van het probleem: drie bollen waarvan
de middelpunten in hetzelfde vlak liggen, die twee aan twee een kegel bepalen.
[einde Opmerking]
Bewijs: zie figuur 17.
| figuur 17 | 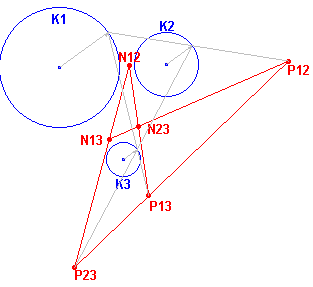 |
De drie cirkels K1, K2, K3 zijn bepaald
door hun middelpunten en stralen. Lijnen door overeenkomstige stralen bepalen de in- en
uitwendige gelijkvormigheidspunten. Volgens de eigenschap in paragraaf 7.2 zijn de uitwendige gelijkvormigheidspunten dus collineair. Het product van de factoren van de verschillende homothetie�n moet positief zijn. Met andere woorden, het gestelde geldt eveneens voor twee inwendige en het overblijvende uitwendige gelijkvormigheidspunt. � |
| Gevolg De mogelijkheden voor drie cirkels zijn: |
| cirkel 1 | cirkel 2 | cirkel 3 | as | |
| + | + | + | P12P13P23 | |
| + | - | - | P23N13N12 | |
| - | + | - | P13N23N12 | |
| - | + | - | P12N23N13 |
Er zijn dus (maximaal) 4 collineatie-assen, ook wel gelijkvormigheidsassen
genoemd.
[einde Gevolg]
Klik hier ![]() voor een animatie van de stelling van
d'Alembert.
voor een animatie van de stelling van
d'Alembert.
Opmerking
De stelling van d'Alembert is onder andere van belang bij de oplossing van het algemene
geval van het Raakprobleem van Apollonius (constructie van alle
cirkels die raken een drie gegeven cirkels).
[einde Opmerking]
7.4. De stelling van Desargues ![]()
| Definities Twee driehoeken ABC en A'B'C' heten (punt)perspectief vanuit een punt P (Eng. copolair) als de lijnen AA', BB', CC' door het punt P gaan. Twee driehoeken ABC en A'B'C' heten lijnperspectief (Eng. coaxial) als de snijpunten van de lijnenparen (AB, A'B'), (AC, A'C") en (CA, C'A') collineair zijn. |
| Stelling van Desargues Twee driehoeken die puntperspectief zijn, zijn ook lijnperspectief (en omgekeerd). |
Bewijs: zie figuur 18a.
| figuur 18a | 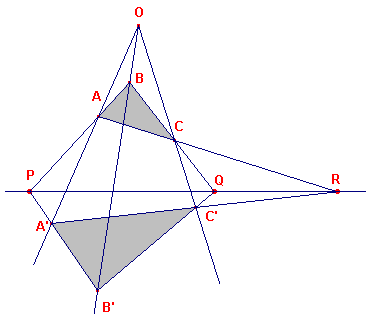 |
De driehoeken ABC en A'B'C' zijn puntperspectief in het punt O P,Q,P zijn de snijpunten van de overeenkomstige zijden. Nu moeten P,Q,R collineair zijn. We beschouwen de driehoeken BCO, CAO en OAB met opvolgend de transversalen QC'B', RC'A' en PA'B'. Volgens de stelling van Menelaos hebben we dan (BCQ).(COC').(OBB') = 1 (CAR).(AOA').(OCC') = 1 (ABP).(BOB').(OAA') = 1 Vermenigvuldigen we de linker en rechter leden van deze uitdrukkingen, dan vinden we (BCQ)(CAR)(ABP) = 1 De punten P,Q,R zijn dus collineair. |
Omgekeerd.
Stel P, Q, R zijn collineair. Zij O het snijpunt van AA' en CC'. We moeten nu laten zien,
dat BB' ook door O gaat.
De driehoeken APA' en CQC' zijn puntperspectief met R als perspectiefpunt, immers de
lijnen AC, PQ, A'C' gaan door R.
Volgens (het hierbovenstaande eerste deel van) de stelling van Desargues zijn dan de
snijpunten van AP en CQ (=B), AA' en CC' (=O), PA' en QC' (=B') collineair.
O ligt dus op BB'. �
Klik hier ![]() voor een animatie van de stelling van
Desargues.
voor een animatie van de stelling van
Desargues.
Opmerkingen
[1]
De stelling van Desargues (Girard
Desargues, 1591-1661, Frankrijk; gepubliceerd in 1636), speelt een
belangrijke rol (oa. als axioma) in de projectieve meetkunde en bij het onderzoek naar de
gronslagen van de meetkunde.
Klik hier voor een
("projectief") bewijs van de stelling gebaseerd op een pooltransformtie.
[2]
Klik hier voor een behandeling van de Gegeneraliseerde
stelling van Desargues.
| figuur 18b | 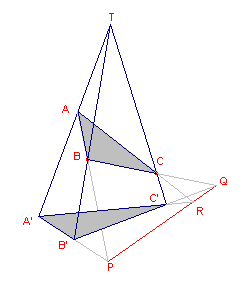 |
[3] Een fraaie illustratie van de Stelling van Desargues vinden we in de stereometrie. Een piramide T.A'B'C' wordt gesneden door een vlak ABC dat niet evenwijdig is met het grondvlak. De beide vlakken ABC en A'B'C' snijden elkaar volgens een rechte lijn, waarop uiteraard de snijpunten P, Q, en R liggen. |
[einde Opmerkingen]
7.5. De Stelling van Pascal voor cirkels ![]()
De stelling van Pascal (voor cirkels) (Blaise Pascal, 1623-1662, Frankrijk) is wellicht (naast
de Cirkel van Feuerbach) de stelling waaraan de meest fraaie
resultaten kunnen worden ontleend.
Algemeen geformuleerd luidt de stelling
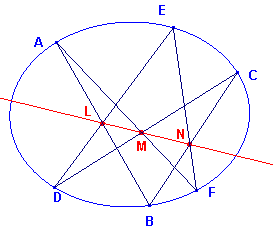
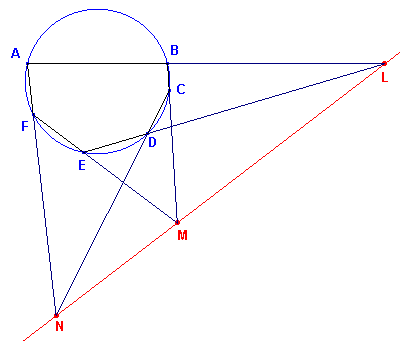
| Stelling van Pascal Van een zeshoek (niet noodzakelijk convex) waarvan de hoekpunten op een kegelsnede liggen, zijn de snijpunten van de drie paren overstaande zijden verschillend en collineair (en omgekeerd) |
| figuur 19a | figuur 19b |
 |
 |
De stelling kan algemeen bewezen worden door gebruik te maken van de theorie der
projectieve meetkunde.
Maar als de hoekpunten van zeshoek liggen op een cirkel, dan kunnen we een eenvoudig
bewijs geven op basis van de Stelling van Menelaos.
| Stelling van Pascal voor cirkels Van een zeshoek (niet noodzakelijk convex) waarvan de hoekpunten op een cirkel liggen, zijn de snijpunten van de drie paren overstaande zijden verschillend en collineair. |
Klik hier voor een behandeling van deze stelling (inclusief een animatie) en enkele gevolgen ervan.