Het raakprobleem van Apollonius
Overzicht ][ Inversie | Geschiedenis | Meetkunde
| Zie ook de pagina "Raakprobleem(2)"
waarop enkele constructies worden behandeld op basis van standaard bewerkingen, zoals
vermenigvuldiging en machten. Bij de deelproblemen (zie paragraaf 2) wordt verwezen naar deze standaard oplossingen. |
1. Inleiding
![]()
In twee verloren gegane boeken, getiteld De Tactionibus (Over aanrakingen),
beschrijft Apollonius van Perga (~262 - ~190 vC) een beroemd
geworden raakprobleem :
| Gegeven drie dingen, waarvan elk een punt, een lijn of een cirkel kan zijn. Bepaal een cirkel die door elk der gegeven punten gaat en die de gegeven lijnen of cirkels raakt. Zie figuur 3. |
Voor een reconstructie van de inhoud van de boeken van Apollonius zie Th. Heath, History
of Greek Mathematics I, pg 182 ev.
Ook eerdere wiskundigen hebben zich uiteraard met het raakprobleem bezig gehouden; oa.
- Francois Viete, ook wel Vieta (1540-1603, Frankrijk), heeft getracht het
werk van Apollonius te reconstrueren (1600).
- C.F. Gauss, Complete Works, vol. IV, pg 399
- J. Gergonne, Annales de Math�matiques, vol. IV (De oplossing
van het probleem zoals Gergonne dat deed, wordt, met weglating van de vele details,
weergegeven in paragraaf 3)
- J. Petersen, Methoden und Theorien
2. Overzicht
deelproblemen ![]()
We kunnen het probleem opsplitsen in de volgende gevallen:
| punten | lijnen | cirkels | code | standaard | |||||
| I. | 3 | - | - | A300 | |||||
| II. | 2 | 1 | - | A210 | I | S210 | |||
| III. | 2 | - | 1 | A201 | I | S201 | |||
| IV. | 1 | 2 | - | A120 | I | S120 | |||
| V. | 1 | - | 2 | A102 | I | S102 | |||
| VI. | 1 | 1 | 1 | A111 | I | S111 | |||
| VII. | - | 3 | - | A030 | |||||
| VIII. | - | 2 | 1 | A021 | |||||
| IX. | - | 1 | 2 | A012 | |||||
| X. | - | - | 3 | A003 |
Alle gevallen kunnen met, zij het soms niet eenvoudige, elementaire constructiemethoden
worden opgelost (zie daarvoor ook de pagina "Raakprobleem(2)"),
maar voor de meeste gevallen ligt het gebruik van inversie
toch zeker voor de hand ligt (deze zijn hierboven met een I aangegeven).
Overigens kunnen we alle gevallen tot ��n terug brengen door punten op te vatten als
cirkels met een straal gelijk aan 0 en rechte lijnen als cirkels met een oneindig grote
straal (in beide gevallen spraken we dan van ontaarde cirkels).
Dat de gevallen waarbij geen punt betrokken is, niet direct met het gebruik
van inversie kunnen worden opgelost, ligt eigenlijk voor de hand. Immers, bij inversie
worden lijnen meestal op cirkels en cirkels op lijnen afgebeeld. Passen we op deze
gevallen inversie toe, dan verandert er meestal niet veel aan het probleem.
Soms echter kan een bijzondere ligging en/of het handig kiezen van de inversiecirkel,
evenwel inversie toelaten (zie A003).
I - A300 - drie punten
![]()
Eenvoudiger kan het niet.
De gevraagde cirkel is de omgeschreven cirkel van de driehoek met die punten als
hoekpunten.
Als de drie punten collineair zijn, dan valt de gevraagde (ontaarde) cirkel samen met de
drager van de punten.
II - A210 - twee punten P en Q en
een lijn l ![]()
Zie figuur A210.
| figuur A210 |  |
Zij R het voetpunt van de loodlijn uit P op l. We kiezen nu de cirkel met middelpunt P en straal PR als inversiecirkel. Door deze
inversie gaat de lijn l over in een cirkel l' en het punt Q in een punt
Q'. Opmerking |
III - A201 - twee punten P en Q en
een cirkel K ![]()
Zie figuur A201a, waarin we de beide punten buiten de cirkel K plaatsen.
| figuur A201 a |
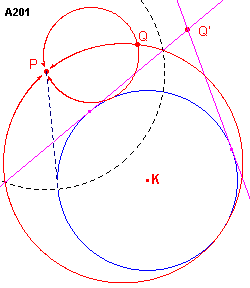 |
We kiezen het punt P als centrum van inversie en de macht van P tov. de
cirkel K als inversiemacht. Door deze inversie gaat de cirkel K over in zichzelf en het
punt Q in een punt Q'. Ook indien beide punten binnen K liggen, kunnen we het probleem oplossen. De macht van
P is hier negatief, zodat we eerst een inversie toepassen met de cirkel K zelf als
inversiecirkel. |
| figuur A201 b |
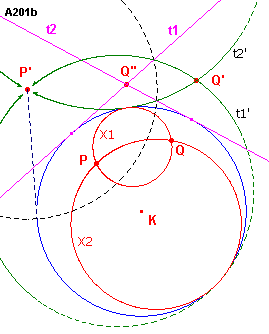 |
De punten P', Q' zijn de beelden van P, Q bij inversie ten opzichte van
cirkel K. We kiezen nu P' als centrum van de inversie, waarvan de inversiemacht gelijk is aan de macht van P' ten opzichte van K. Bij deze laatste inversie gaat K over in zichzelf. Q' wordt hierbij afgebeeld op het punt Q". We gaan nu op dezelfde manier te werk als beschreven bij A201a. t1, t2 zijn de raaklijnen uit Q" aan K. De beide inversies geven dan opvolgend de beelden t1', t2' (cirkels) en X1, X2 (de gevraagde cirkels). Opmerking |
IV - A120 - een punt P en twee
lijnen l en m ![]()
Zie figuur A120/
| figuur A120 | 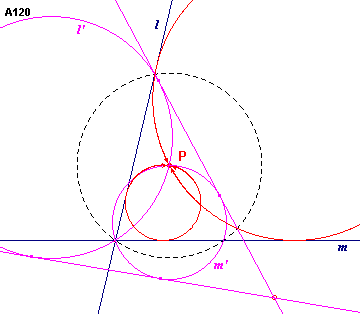 |
We kiezen het punt P als middelpunt van de inversiecirkel, die we laten
gaan door het snijpunt van de lijnen l en m. Door deze inversie gaan
de lijnen l, m over in twee (elkaar snijdende cirkels l' en m'. Opmerking |
V - A102 - een punt P
en twee cirkels K1 en K2 ![]()
Zie figuur A102.
| figuur A102 | 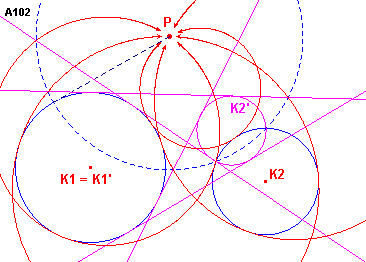 |
We kiezen het punt P als centrum van de inversie met als inversiemacht de
macht van P tov. de cirkel K1. Door deze inversie gaat de cirkel K1
over inzelf en wordt de cirkel K2 afgebeeld op een cirkel K2'. Opmerking |
VI - A111 - een punt P,
een lijn l en een cirkel K ![]()
Zie figuur A111.
| figuur A111 | 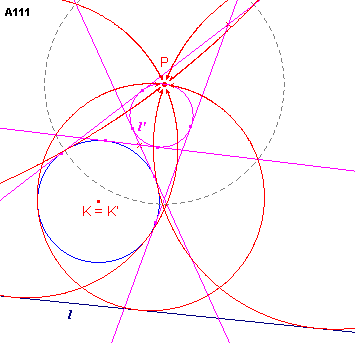 |
We kiezen het punt P als inversiecentrum en de macht van P ten opzichte
van de cirkel K als inversiemacht. Door deze inversie gaat de cirkel K over in zichzelf,
terwijl de lijn l wordt afgebeeld op een cirkel l'. Opmerking |
VII - A030 - drie lijnen
![]()
De (maximaal vier) te construeren cirkels zijn de incirkel en de drie uitcirkels
van de driehoek die door de drie lijnen wordt ingesloten.
VIII - A021 - twee lijnen l, m
en een cirkel K ![]()
Zie figuur A021.
| figuur A021 | 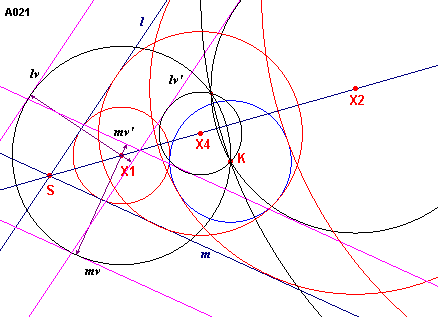 |
We kunnen dit geval terugbrengen tot geval IV, A120, en wel door de volgende redenering. Als een cirkel X moet raken
aan l en m en aan de cirkel K, dan bestaat er een (met X) concentrische
cirkel door het middelpunt van K die raakt aan de lijnen lv en mv
(de over de straalafstand van K evenwijdig verschoven lijnen l en m). |
IX - A012 - een lijn l en
twee cirkels K1 en K2 ![]()
Zie figuur A012.
| figuur A012 | 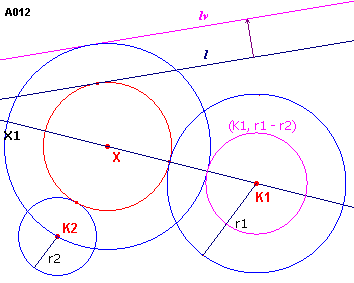 |
We onderstellen hierbij, dat voor de stralen van r1 en r2
van K1 en K2 geldt r1 > r2. We kunnen nu de constructie terugbrengen tot geval VI, A111, en wel door de volgende redenering. Een cirkel X die raakt aan l en aan K1
en K2, is concentrisch met een cirkel X1 die raakt aan lv
(de lijn die evenwijdig aan l verschoven is over de afstand r2), gaat
door K2 en raakt aan de cirkel (K1, r1-r2). |
| In figuur A012b zijn 4 van deze 8 mogelijke oplossingen weergegeven. |
| figuur A012 b |
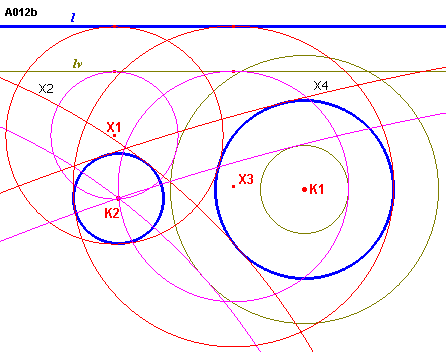 |
Het zijn de 4 cirkels die als basis de raakcirkels hebben aan lv
(de hulpcirkels Xi'). Van deze hulpcirkels Xi' is de straal verminderd met r2. X1'
en X2' raken aan de cirkel (K1, r1+r2) Aanloog kunnen de overige 4 cirkels worden geconstrueerd. |
X - A003 - drie cirkels K1,
K2 en K3 ![]()
We lossen dit probleem eerst op in het geval de drie cirkels door ��n punt M gaan en de
centralen niet samenvallen. Zie figuur A003a.
| figuur A003 a |
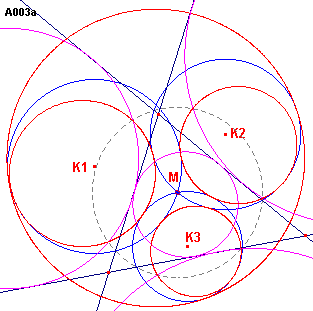 |
Kiezen we M als centrum van een inversie met een
inversiecirkel die de drie cirkels snijdt, dan gaan de cirkels Ki over in
rechte lijnen, die een driehoek insluiten. |
Zoals opgemerkt kunnen we soms door een bijzondere ligging het probleem terugbrengen
tot een eerder behandeld geval.
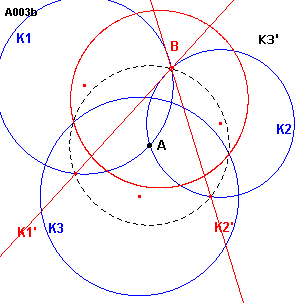
In figuur A003b zien we dat de drie cirkels elkaar twee aan twee snijden.
| figuur A003 b |
figuurA003 c |
|
 |
 |
Snijden K1 en K2 elkaar in A en B dan kunnen we A als centrum van
inversie en de lengte van AB als inversiemacht nemen.
Hierdoor gaan K1, K2 over in de rechte lijnen K1', K2',
terwijl K3 overgaat in een nieuwe cirkel K3'.
Het probleem is hierdoor teruggebracht tot geval VIII, A021, twee
lijnen en een cirkel.
Hieraan is evenwel gemakkelijk te zien, dat het algemene geval maximaal 8 oplossingen
toelaat.
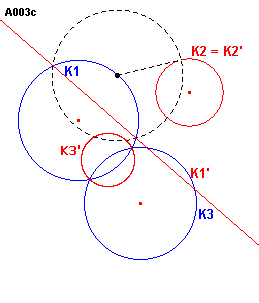
Indien de cirkels elkaar niet snijden (zie figuur A003c), dan kunnen we reduceren tot geval IX, A012, een lijn en twee cirkels, door het inversiecentrum te
plaatsen op (bijvoorbeeld) K1 en de inversiemacht gelijk te nemen aan de macht
van het centrum ten opzichte van (bijvoorbeeld) K2.
Hierdoor gaar K1 over in de rechte lijn K1', K2 in
zichzelf en K3 in een nieuwe cirkel K3'.
3. Algemene
oplossing van A003 ![]()
Voor een algemene oplossing van het geval X, A003, kunnen we gebruik maken van elementaire
eigenschappen van homothetie�n (dit zijn vermenigvuldigingen tov. een punt) en van de hoofdstelling van de pooltheorie (die evenwel samenhangt met de theorie der inversies).
De oplossing van het raakprobleem valt in vier delen uiteen:
3.1. Raking van drie cirkels en de
gelijkvormigheidspunten van twee ervan ![]()
We gaan uit van twee cirkels A en B, waaraan een derde cirkel X raakt (opvolgend in de
punten P en Q); zie figuur 1.
| figuur 1 | 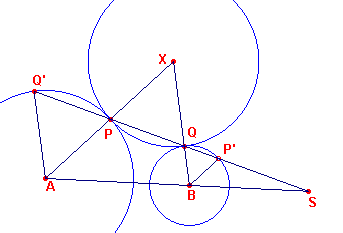 |
De lijn PQ snijdt AB in het punt S en de cirkels A en B ook nog in Q' en
P'. Duidelijk is, dat de driehoeken APQ', XPQ, BP'Q gelijkvormig zijn (gelijkbenige driehoeken). Het punt S is dus het (uitwendig) gelijkvormigheidspunt van de cirkels A en B. Zodat: SP' : SP = SQ : SQ' De producten SP � SQ en SP' � SQ' zijn dus aan elkaar gelijk. Stel ze beide gelijk aan w. Nu is w2 = (SP' � SQ) � (SP � SQ') |
en dit is het product van de machten van S ten opzichte van de cirkels A en B. w2
= I is dus constant. Geldt ook
SP � SQ = �I
eveneens constant. Deze waarde is dus onafhankelijk van de ligging van de cirkel X (en van
de raakpunten)..
We komen zo tot de volgende in paragraaf 3.2 te gebruiken
| Raakcirkel-stelling Het (uit- of inwendig) gelijkvormigheidspunt van twee cirkels heeft dezelfde macht ten opzichte van alle cirkels die aan beide cirkels raken. De lijn die de raakpunten verbindt, gaat steeds door het betreffende gelijkvormigheidspunt. |
3.2. Verband met machten ![]()
Gaan we uit van het paar cirkels X1 en X2 dat opvolgend raakt aan de
cirkels A, B, C.
Raken de cirkels X1, X2 aan de drie cirkels in opvolgend P1
en P2, Q1 en Q2, R1 en R2, dan gaan
de koorden P1P2, Q1Q2, R1R2
door het machtpunt van A,B,C. Dit volgt voor het paar X1,
X2 en telkens cirkel A, B of C daaraan rakend uit de Raakcirkel-stelling.
Drie van de zes gelijkvormigheidspunten van A,B,C liggen telkens op een rechte lijn,
een gelijkvormigheidsas van de drie cirkels (dit is de Stelling
van d'Alembert).
Noteren we zo'n gelijkvormigheidspunt van A,B met S(AB), dan geldt eveneens volgens de Raakcirkel-stelling:
S(AB) heeft gelijke machten ten opzichte van X1 en X2
S(BC) heeft gelijke machten ten opzichte van X1 en X2
S(CA) heeft gelijke machten ten opzichte van X1 en X2
De gelijkvormigheidsas waarop deze drie punten, liggen is dus de machtlijn van X1
en X2.
3.3. Verband met de pooltheorie
![]()
Zie hiervoor figuur 2.
| figuur 2 | 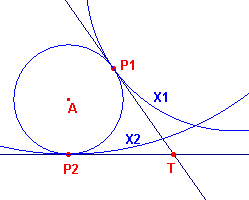 |
Zij T het snijpunt van de (gemeenschappelijke) raaklijnen in P1
en P2 aan cirkel A (en aan X1 opvolgend X2). Het punt T ligt ook op de machtlijn van X1 en X2, immers T heeft gelijke machten ten opzichte van cirkel A. Maar T is eveneens de pool van de lijn P1P2 ten opzichte van de cirkel A. Analoog kan worden geredeneerd voor de raakpunten op de cirkels B en C. |
3.4. De constructie van de raakcirkels ![]()
Op basis van hetgeen gevonden is in de paragraaf 3.1, paragraaf
3.2 en paragraaf 3.3 kunnen we de constructie dus als volgt
beschrijven:
Het resultaat van het bovenstaande staat in figuur 3.
| figuur 3 |
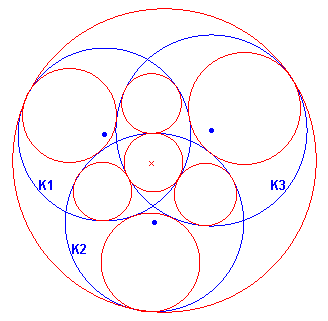 |
Opmerkingen
[1]
De behandeling van de oplossing van het Raakprobleem van Apollonius in paragraaf
3 komt overeen met de wijze waarop het probleem is opgelost door Gergonne.
[2]
Indien de drie cirkels in geval A003 elkaar twee aan twee raken hebben we de Cirkelstelling
van Descartes. Er zijn dan twee oplossingen van het raakprobleem. Deze
oplossingen worden Soddy-cirkels (naar Sir Frederick Soddy, 1877-1956,
Engeland) genoemd.
Zie hiervoor de pagina "Soddy-cirkels".
[3] Zie ook de pagina "Raakprobleem(2)"
waarop enkele constructies worden behandeld op basis van standaard bewerkingen, zoals
vermenigvuldiging en machten.
[einde Opmerkingen]