De macht van een punt tov. een cirkel

Overzicht  ][  Meetkunde

Zie ook het Cabri-werkblad "Machtlijn van twee cirkels".

0. Overzicht begin pagina

  1. Definitie: macht van een punt cabrisignal.gif (160 bytes)
  2. Gevolgen
  3. Machtlijn cabrisignal.gif (160 bytes)
           Machtpunt en machtcirkel
  4. Constructie machtlijn cabrisignal.gif (160 bytes)
  5. Hoogtepunt cabrisignal.gif (160 bytes)

1. Definitie: macht van een punt begin pagina

Definitie
Onder de macht van een punt P ten opzichte van een cirkel met middelpunt M en straal R wordt verstaan het getal
   m(P) = d2 - R2
waarin d = PM.
.
figuur 1 figuur 1 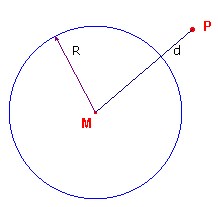Uit deze definitie volgt
  • m(P) > 0 DESDA P ligt buiten de cirkel
  • m(P) = 0 DESDA P ligt op de cirkel
  • m(P) < 0 DESDA P ligt binnen de cirkel

Opmerking
De macht van een punt P ten opzichte van een cirkel C wordt ook wel een genoteerd als
   m(P, C)
[einde Opmerking]

Klik hier >Animatie< voor een CabriJavapplet van de macht van een punt ten opzichte van een cirkel.

2. Gevolgen begin pagina

Stelling 1
Een punt buiten een cirkel verdeelt alle koorden die bij verlenging door dat punt uitwendig in twee stukken met een constant product
.
figuur 2a 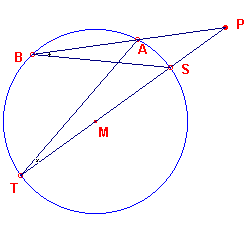figuur 2 Bewijs:
Zij AB een koorde die bij verlenging door P gaat. Nu is hoek ATP = hoek SBP. Immers, beide omtrekshoeken staan op dezelfde boog AS.
Dus is driehoek BPS gelijkvormig met driehoek TPA. Daaruit volgt
   BP/PS = TP/PA
of
PA x PB = PS x PT
= (d - R) (d + R)
= d2 - R2

Het product van de stukken is dus constant. ?
.
Gevolg van Stelling 1
De macht van een punt buiten een cirkel is gelijk aan het kwadraat van de lengte van een raaklijnstuk uit dat punt aan die cirkel.
In figuur 2b: PA x PB = PS2 .

Bewijs:

figuur 2b 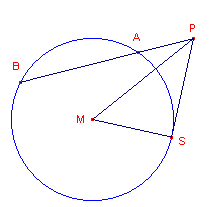macht2b.gif (1255 bytes) Driehoek PSM is rechthoekig in S.
Volgens de stelling van Pythagoras is dan:
   PS2 = PM2 - SM2
dus
   PS2 = d2 - R2 ?

Ook voor een punt binnen de cirkel kunnen we eenzelfde eigenschap bewijzen.
Merk echter op, dat het punt P nu kan samenvallen met het middelpunt van de cirkel.

Stelling 2
Een punt binnen een cirkel verdeelt alle koorden door dat punt in twee stukken met een constant product.
figuur 3a 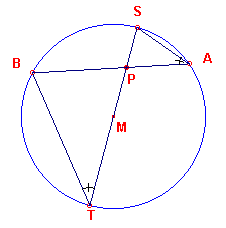figuur 3 Bewijs:
Zij AB nu een koorde door het punt P.
Als P samen valt met M is PA x PB = R2, dus constant.
Valt P niet samen met M, dan bekijken we de driehoeken PAS en PBT. Hierin is hoek A gelijk aan hoek T, zodat geldt PAS ? PTB. Hieruit volgt PA/PT = PS/PB.
Of
PA x PB = PS X PT
= (R - d)(R + d)
= R2 - d2

Het product van de stukken is dus constant. ?

Wegens de definitie van macht kunnen we dus stelling 1 en stelling 2 ook als volgt formuleren.

Stelling 3
De macht van een punt P binnen een cirkel is gelijk aan het tegengestelde van het product van de stukken waarin P een willekeurige koorde door P verdeelt.
De macht van een punt P buiten een cirkel is gelijk aan het product van de stukken waarin een willkeurige koorde die door P gaat, uitwendig verdeelt.
De macht van een punt op de cirkel is gelijk aan 0.

Opmerking
Rekentechnisch is de macht van een punt binnen een cirkel negatief (zie de definitie), immers d < R.
[einde Opmerking]

Gevolg van Stelling 2

figuur 3b 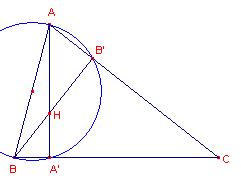macht3b.gif (1316 bytes) Zie figuur 3b.
In driehoek ABC geldt voor het hoogtepunt H:
HA . HA' = HB . HB' = HC . HC'.

[einde Gevolg]

3. Machtlijn begin pagina

Stelling 4
De meetkundige plaats der punten waarvoor het verschil van de kwadraten der afstanden tot twee gegeven punten constant (c2) is, is een loodlijn op de lijn door deze twee punten.

Bewijs:
Zijn de twee gegeven punten M en N, waarbij MN = d, en is l de lijn door M en N
We tonen eerst aan, dat op l een punt S ligt dat tot de meetkundige plaats behoort (zie figuur 4).
Voor S moet dan gelden SM2 - SN2 = c2. Hieruit volgt, dat SM > SN, zodat S alleen kan liggen op het verlengde van MO, waarbij O het midden is van MN.
Stellen we SM = x, dan geldt voor elk punt S op het verlengde van MO: SM = ?d + x en SN = | ?d - x |.

figuur 4 figuur 4 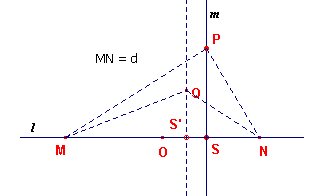Nu is SM2 - SN2 = (?d + x)2 - (?d - x)2 = 2dx
Wil S op de meetkundige plaats liggen, dan moet dus voldaan zijn aan
   2dx = c2
of
   x = c2/(2d)
Er ligt dus inderdaad een punt (S) van de meetkundige plaats op de lijn l.

Zij nu de lijn m door S loodrecht op l.
Is P een punt van m dat niet met S samenvalt.
Dan is:
PM2 - PN2 = (SP2 + SM2) - (SP2 + SN2)
= SM2 - SN2
= c2

Dus voor elk punt P van de lijn m is PM2 - PN2 = c2

Omgekeerd: Stel Q is een punt dat niet op l ligt en waarvoor geldt QM2 - QN2 = c2 (zie ook figuur 4)
Is S' het voetpunt van de loodlijn uit Q op l, dan is
   S'M2 - S'N2 = (QM2 - S'Q2) - (QN2 - S'Q2) = QM2 - QN2 = c2.
Het punt S' valt dus samen met het punt S, want het enige punt op l waarvor die relatie geldt, is het punt S.
Hieruit volgt weer dat de loodlijn uit Q samenvalt met m, zodat Q dus een punt is van m.

De lijn m is dus de meetkundige plaats van de punten P, waarvoor geldt PM2 - PN2 = c2. ?

Met behulp van stelling 4 kunnen we een stelling bewijzen over de macht van een punt ten opzichte van twee cirkels.

Stelling 5
De meetkundige plaats van de punten die gelijke machten hebben ten opzichte van twee niet-concentrische cirkels, is een loodlijn op de centraal van beide cirkels.
Deze meetkundige plaats heet de machtlijn van die cirkels.

Klik hier Animatie voor een CabriJavapplet van de machtlijn van twee cirkels.

Bewijs: We onderscheiden twee gevallen: (1) R1 ? R2 en (2) R1 = R2, waarbij R1 de straal is van de cirkel met middelpunt M en R2 de straal is van de cirkel met middelpunt N (zie figuur 5).

figuur 5 figuur 5 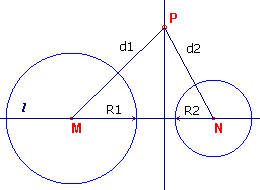(1) R1 ? R2; we kunnen hierbij onderstellen, dat R1 > R2.
Berekening van R12 - R22 levert nu een positief getal; stel dat gelijk aan c2.
Heeft het punt P gelijke machten ten opzichte van de cirkels en noemen we PM = d1 en PN = d2, dan is
   d12 - R12 = d22 - R22
Waaruit volgt, dat d12 - d22 = R12 - R22 = c2.
Volgens stelling 4 is nu de meetkundige plaats van de punten P een loodlijn op de lijn l (de centraal).

(2) R1 = R2 (= R)
Heeft P gelijke machten ten opzichte van beide cirkels, dan is
   d12 - R2 = d22 - R2
Waarut volgt d12 = d22. Dus d1 = d2.
In dit geval is de meetkundige plaats van de punten P (zoals bekend) de middelloodlijn van het lijnstuk MN. ?

Opmerking
Bij twee concentrische cirkels kunnen we geen enkel punt P bepalen met gelijke machten tov. beide cirkels Immers, met PM = PN = d vinden we nu
   m(P, M) = d2 - R12
   m(P, N) = d2 - R22
Hieruit zou volgen, dat de beide cirkels gelijke stralen hebben. Er is dus geen sprake van twee cirkels.
[einde Opmerking]

Gevolg
Als twee cirkels elkaar snijden, dan hebben de snijpunten een macht 0 ten opzichte van beide cirkels.
? De machtlijn van twee snijden cirkels gaat dus door de snijpunten van die cirkels
Als twee cirkels elkaar raken, dan heeft het raakpunt een macht 0 ten opzichte van beide cirkels.
? De machtlijn van twee rakende cirkels is dus de gemeenschappelijke raaklijn van beide cirkels.
Zie paragraaf 3b voor de constructie van de machtlijn als de cirkels elkaar niet snijden.
[einde Gevolg]

Stelling 6 begin pagina
De machtlijnen van drie cirkels waarvan de middelpunten niet collineair zijn, gaan door ??n punt.
Dit punt is het machtpunt van de drie cirkels.

Bewijs: (zie figuur 6)

figuur 6 figuur 6 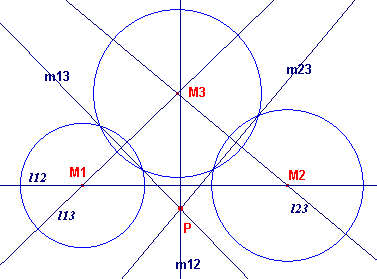De middelpunten M1, M2, M3 zijn niet collineair, dus de lijnen l12, l13, l23 (de centralen) snijden elkaar.
De lijnen m12 en m23, die loodrecht staan op l12 en l23 snijden elkaar dus ook. Zij dit snijpunt het punt P.
P heeft nu niet alleen gelijke machten ten opzichte van cirkel M1 en cirkel M2 (P ligt op m12), maar ook ten opzichte van cirkel M2 en cirkel M3 (P ligt op m23).

Hieruit volgt, dat P dus ook gelijke machten heeft ten opzichte van cirkel M1 en cirkel M3.
P ligt dus ook op de machtlijn m13 van de cirkels M1 en M3.
Met andere woorden: de lijn m13 gaat dus ook door P. ?

Opmerkingen
[1]
Stelling 6 is onder andere van betekenis bij de oplossing van het algemene geval van het Raakprobleem van Apollonius (constructie van de cirkels die raken aan drie gegeven cirkels).
[2]
De cirkel met het machtpunt als middelpunt die de drie cirkels loodrecht snijdt heet machtcirkel van de drie cirkels.
Over de machtcirkel in samenhang met de pooltheorie staat een stelling op de pagina "Pool en poollijn".
[einde Opmerkingen]

4. Constructie van de machtlijn begin pagina
We kunnen het machtpunt van drie cirkels gebruiken voor een eenvoudige constructie van de machtlijn van twee cirkels, in ieder geval te gebruiken als de cirkels elkaar niet snijden.

  1. Kies een derde cirkel die beide gegeven cirkels snijdt.
  2. Bepaal de machtlijnen van deze cirkel met de gegeven cirkels.
  3. Bepaal het snijpunt van deze machtlijnen (dit is het machtpunt van de drie cirkels).
  4. Laat een loodlijn neer uit dit punt op de centraal van de gegeven cirkels.
    Deze loodlijn is de machtlijn van de gegeven cirkels.

Klik hier cabrismall.gif (1087 bytes) voor een CabriJavapplet van bovenstaande constructie.

Opmerking]
Zie ook de pagina "Gelijkvormigheid bij cirkels" voor een andere constructie van de machtlijn (met inversie).
[einde Opmerking]

5. Hoogtepunt van een driehoek begin pagina
Stelling 6 geeft in een andere configuratie een eenvoudig bewijs van de concurrentie van de hoogtelijnen van een driehoek:

Stelling 7
De hoogtelijnen van een driehoek gaan door ??n punt, het hoogtepunt van de driehoek.

Bewijs: (zie figuur 7)

figuur 7 figuur 7 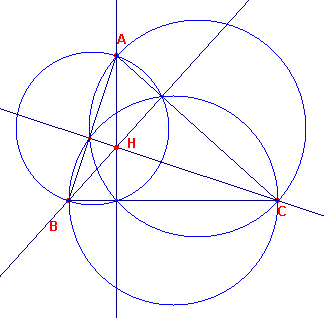De machtlijnen van de drie cirkels met de zijden van de driehoek als middellijn gaan door ??n punt. De machtlijnen zijn de hoogtelijnen van driehoek ABC. ?

Opmerking
Zie ook het Gevolg van Stelling 2.
H is dus het machtpunt van de drie cirkels.
Zie verder Stelling 8.
[einde Opmerking]

Stelling 7 kan ook iets algemener worden geformuleerd.

Stelling 8
Het hoogtepunt van een driehoek is het machtpunt van de drie cirkels op hoektransversalen door de hoekpunten van die driehoek.

Bewijs: zie figuur 8.

figuur 8 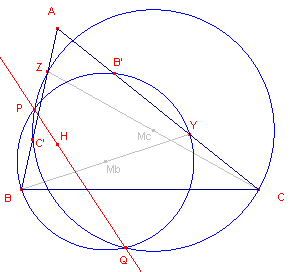macht8.gif (2919 bytes) De punten Y (op AC) en Z (op AB) bepalen twee hoektransversalen.
De punten Mb en Mc zijn de cirkels met BY en CZ als middellijn.
Deze cirkels snijden elkaar in P en Q.
De lijn PQ gaat nu door het punt H.

De cirkels snijden de zijden behalve in Y en Z ook nog in B' en C' (de voetpunten van de hoogtelijnen uit B en C).
Nu is HB . HB' = HC . HC' (zie gevolg van Stelling 2).
Het punt H heeft dus gelijke machten tov. de beide cirkels.
Het punt H ligt dus op de machtlijn PQ van deze cirkels.

Kiezen we nu een derde hoektransversaal (door A), dan is H dus het machtpunt van de drie cirkels. ?

Klik hier cabrismall.gif (1087 bytes) voor een CabriJavapplet van Stelling 8.

begin pagina
[machtpunt.htm] laatste wijziging op: 25-03-2006