Gergonne-punt, Gergonne-driehoek, Gergonne-lijn
Overzicht ][ Transversalen | Tucker-cirkels | Meetkunde
| figuur 1 | 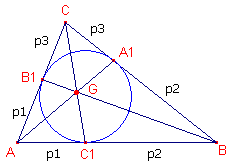 |
| . |
| Stelling 1 De hoektransversalen door de raakpunten van de incirkel van een driehoek met de zijden, zijn concurrent. Hun snijpunt heet het punt van Gergonne van de driehoek (naar Joseph Gergonne, 1771-1859, Frankrijk). |
Bewijs: zie figuur 1.
Volgens de stelling van Ceva is nu: (ABC1)(BCA1)(CAB1) =
- p1/p2 . p2/p3 . p3/p1
= -1.
De transversalen zijn dus concurrent. �
Opmerkingen
[1] Bovenstaand bewijs staat ook op de pagina "Transversalen".
[2] Een tweede bewijs staat, als een bijzonder geval van de Stelling van
Brianchon, op de pagina "Stelling van Pascal".
[3] Zie hiervoor ook de pagina "Barycentrische
co�rdinaten".
[einde Opmerkingen]
2.
Gergonne-driehoek ![]()
We geven eerst het bewijs van de volgende hulpstelling.
| Hulpstelling De raaklijnen in twee hoekpunten van een driehoek aan de omcirkel snijden elkaar op de symmediaan van het derde hoekpunt. |
Nb.
De symmedianen van een driehoek snijden elkaar in het punt K van Lemoine.
Bewijs: zie figuur 2.
| figuur 2 | 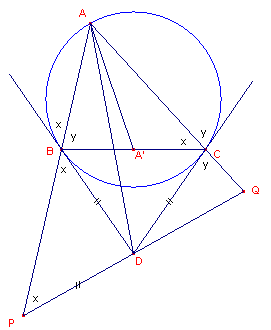 |
De raaklijnen in B en C snijden elkaar in D. We moeten aantonen, dat AD
een symmediaan is van driehoek ABC. We doen dit door te bewijzen, dat hoekBAD' = hoek CAA', waarbij A' het midden is van BC. We kiezen het punt P op het verlengde van AB zo, dat PD=BD. PD snijdt het verlengde van AC in Q. De gelijke hoeken in de figuur zijn aangegeven met x en y. De driehoeken ABC en APQ hebben nu twee hoeken gelijk (namelijk hoek A en hoek C. Dus is hoek Q gelijk aan hoek B. Driehoek CDQ is dus eveneens gelijkbenig, waardoor D het midden is van PQ. AD is dus mediaan (zwaartelijn) van driehoek APQ. De driehoeken ABC en AQP zijn gelijkvormig. De, door de mediaan naar de overeenkomstige zijde, gesplitste driehoeken daarvan (AA'C en ADP) dus ook. De hoeken bij A in beide driehoeken zijn dus gelijk. � |
Opmerking
Deze hulpstelling wordt op de pagina "Isogonalen" (als Stelling 10) bewezen met behulp van de
theorie van pool en poollijn.
[einde Opmerking]
| Definitie De driehoek gevormd door de raakpunten van de incirkel met de zijden van een driehoek heet driehoek van Gergonne van die driehoek. |
| . |
| Stelling 2 Het punt van Gergonne van een driehoek is het symmediaanpunt (punt van Lemoine) van zijn Gergonne-driehoek. |
Bewijs: zie figuur 3.
| figuur 3 | 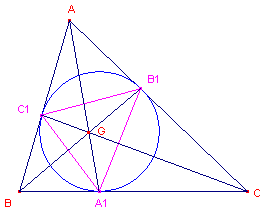 |
De incirkel van driehoek ABC is de omcirkel van de Gergonne-driehoek A1B1C1. Volgens de hulpstelling snijden de raaklijnen in twee van de hoekpunten elkaar op de symmediaan van het derde hoekpunt. Dus: Het punt A, als snijpunt van de raaklijnen in B1 en C1 aan de incirkel, ligt op de symmediaan van A1. AA1 is dus een symmediaan van driehoek A1B1C1. Evenzo ook BB1 en CC1. G is dus symmediaanpunt van driehoek A1B1C1. � |
Opmerkingen
[1]
Stelling 2 wordt gebruikt bij het bewijs over de Adams-cirkel
op de pagina "Tucker-cirkels".
[2]
Zie ook de pagina "Om- en incirkel"
voor een bewijs over het verband tussen de stralen van de om- en incirkel.
Op die pagina wordt ook bewezen, dat het beeld van de omcirkel bij inversie tov. de
incirkel de negenpuntscirkel van de Gergonne-driehoek is.
[einde Opmerkingen]
3. Gergonne-lijn ![]()
Klik hier voor
een behandeling van de Gergonne-lijn en de Nobbs-punten.