Overzicht ][ Inverse afstand | Meetkunde
Zie ook de pagina's "Incirkel" en "Uitcirkels"
1. De afstand tussen de middelpunten
van de om- en incirkel ![]()
| Stelling 1 Zijn (O, R) en (I, r) opvolgend de om- en incirkel van driehoek ABC, dan is OI2 = R2 - 2Rr |
| figuur 1 | 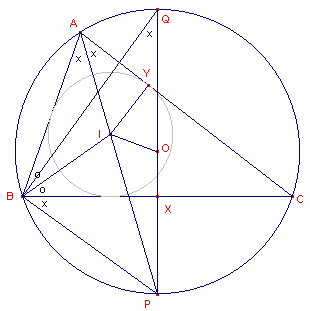 |
In de figuur is x is de grootte van de halve hoek A; o is de grootte van de halve hoek B; PQ is een middellijn van de omcirkel; IY = r en OI = m . Driehoek ABI heeft een buitenhoek bij I, waarvoor geldt �BIP = x + o. Maar ook �IBP = x + o. Driehoek BPI is dus gelijkbenig (PB = PI). We bekijken nu de macht van het punt I ten opzichte van de omgeschreven cirkel (de macht is negatief voor een punt binnen de cirkel): -(R2 - m2) = -(IP x IA) = -(BP x IA) ......(1) Nu zijn de driehoeken BPQ en YIA gelijkvormig (rechte hoek en hoek x gemeenschappelijk), zodat YI : BP = IA : PQ |
Vermenigvuldigen we nu het rechter lid van betrekking (1) met een herleiding op 1 van
deze verhouding, dan vinden we:

Dus R2 - m2 = r . 2R
waaruit volgt:
m2 = R2 - 2Rr
�
Opmerkingen
[1]
Deze formule is het eerst vermeld door Leonard Euler (1707-1783, Zwitserland).
[2]
Zie ook de pagina "Sluitingsstelling van Poncelet"
[3]
Zie ook het artikel "Over de lengte
van OH, OZ en OI in een willekeurige driehoek" (april
2007, PDF-bestand, ca. 97Kb)
[einde Opmerkingen]
2. Driehoeken met dezelfde om- en
incirkel ![]()
| Stelling 2 Bij een inversie tov. de incirkel van de driehoek gaan de zijden en de omcirkel over in vier cirkels met gelijke straal. |
Bewijs:
Zie voor de eigenschappen van de inversie de pagina "Inversie".
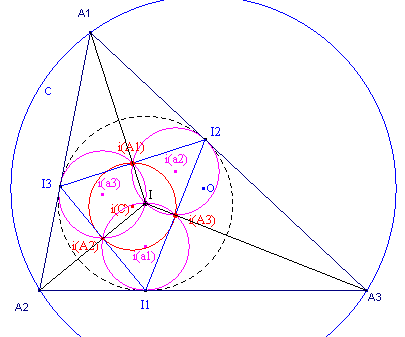 |
De lijn A1A2 gaat door de inversie over in
een cirkel door I en I3 (immers I3 ligt op de
inversiecirkel), en in I3 rakend aan A1A2. De straal van die cirkel is dus gelijk aan � r. Dit geldt mutatis mutandi ook voor de andere zijden van de driehoek. Voor de macht p van I tov. cirkel C (de omcirkel) geldt: p = IO2 - R2 = - 2Rr (zie Stelling 1) Het beeld van C is een productfiguur bij een vermenigvuldiging met factor (k2)/p, waarbij k de macht van de inversie (straal van de inversiecirkel) is. De straal van het beeld van C is dan gelijk aan (r2 / 2Rr) � R = � r. Het beeld van C gaat door de middens van de zijden van driehoek I1I2I3 (immers I1I2I3 is een vlieger). Die middens zijn de beelden van de punten A1, A2, A3 bij de inversie. � Opmerking |
| Stelling 3 ("beperkte" Sluitingsstelling van Poncelet) Zijn twee cirkels O(R) en I(r) zo gelegen, dat R2 - OI 2 = 2Rr dan bestaan er oneindig veel driehoeken met hoekpunten op de eerste cirkel waarvan de zijden raken aan de tweede cirkel. |
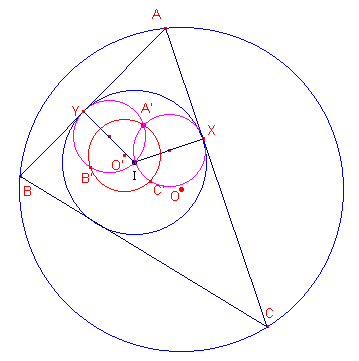 |
We geven een bewijs door middel van constructie. Cirkel O wordt door een inversie tov (I, r) afgebeeld op een cirkel met straal R' = r2 / (OI 2 - R2)�R (zie ook Stelling 2). Op basis van de gegeven relatie is nu R' = � r. Zij nu A' een willekeurig punt van de beeldcirkel O'. De cirkels met straal � r die gaan door A en I, raken beide aan cirkel I (in de punten X en Y). A' is daarbij het midden van XY (in te zien via Thales-cirkels op IX en IY). De punten B' en C' zijn de (tweede) snijpunten van cirkel O' en beide laatste cirkels. Het beeld A van A' bij de inversie ligt op cirkel O. De beelden van B en C van B' en C' bij deze inversie vormen samen met het punt A een driehoek die aan de gestelde eisen voldoet. Omdat A' willekeurig is op cirkel O', zijn er oneindig veel van deze driehoeken. � Klik hier Opmerking |
| [1] | O. BOTTEMA: Hoofdstukken uit de Elementaire Meetkunde, N.V. Servire, Den Haag, 1944 | |
| [2] | H.S.M. COXETER: S.L. GREITZER: Geometry Revisited, MAA, 1969 (Vol. 19) | |
| [3] | DICK KLINGENS: Over de lengte van OH, OZ en OI in een willekeurige driehoek. (PDF-bestand, ca. 97Kb) | |
| [4] | R.A. JOHNSON: Adavanced Euclidean Geometry, Dover Publications, 1960 | |
| [5] | FLOOR. VAN LAMOEN: De Porisme-cirkels (website) | |
| [6] | P. WIJDENES: Vlakke meetkunde voor voortgezette studie, P. Noordhoff N.V., Groningen, 1964 |
4. Download ![]()
Enkele figuren van deze pagina, waaronder de figuur die gebruikt is bij de CabriJavapplet,
kunnen via deze website worden gedownload.
Klik hier om het downloaden te
starten (ZIP-bestand, ca 4kB).