Sluitingsstelling van Poncelet

Overzicht ][ Om- en incirkel | Meetkunde

0. Overzicht begin pagina

  1. Probleemstelling cabrisignal.gif (160 bytes)
  2. Twee hulpstellingen en de stelling van Casey en Hart cabrisignal.gif (160 bytes)
  3. Bewijs van de sluitingsstelling  cabrisignal.gif (160 bytes)
  4. Projectief bewijs van de sluitingsstelling cabrisignal.gif (160 bytes)
  5. Referenties

Zie ook de pagina "Om- en incirkel" voor een bewijs van de (beperkte) Sluitingsstelling via inversie.

1. Probleemstelling begin pagina

Stelling 1
Zij P een punt van cirkel en raken de koorden door P aan twee met die cirkel coaxiale (*) cirkels, dan raken de sluitlijnen van de koorden aan een derde coaxiale cirkel, indien P de cirkel doorloopt.
(Sluitingsstelling van Poncelet,  naar Jean Victor Poncelet, 1788-1867, Frankrijk, gepubliceerd in 1822)
.
figuur 1 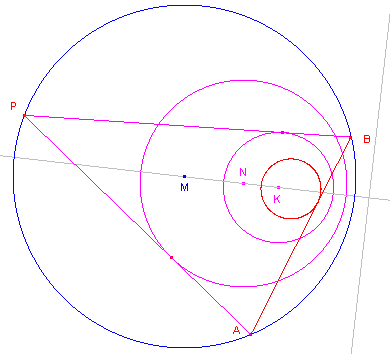sluitstel1.gif (4129 bytes) __________
(*)
Coaxiale cirkels (coaxiaalcirkels) zijn cirkels met dezelfde machtlijn. Men spreekt ook wel van een cirkelbundel.
Zie hiervoor het Cabri-werkblad "Cirkelbundels".
����������
Klik hier Animatie voor een CabriJavapplet van Stelling 1.

Het bewijs van stelling 1, op basis van enkele hulpstellingen, staat in paragraaf 3.

2. Twee hulpstellingen en de stelling van Casey en Hart begin pagina

Definitie
Onder een P-stelsel verstaan we een tweetal cirkels(M,R) en (N,r). Cirkel (M) heet wel de hoofdcirkel van het P-stelsel.
Indien MN = a, dan geven we de cirkel (N,R) aan met (a).
.
Stelling 2 (hulpstelling)
Als d de afstand is van het punt M tot de machtlijn van het P-stelsel, dan geldt
   2ad = R2 + a2 - r2

Bewijs:

figuur 2 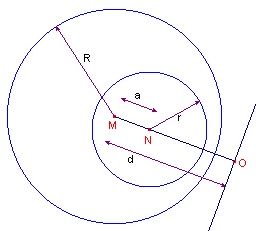sluitstel2.gif (2051 bytes) macht(O, cirkel(M)) = d2 - R2 ......(1)
macht(O, cirkel(N)) = (d - a)2 - r2 ......(2)
(1) = (2), zodat
   d2 - R2 = d2 - 2ad +a2 - r2
waaruit onmiddellijk volgt
   2ad = R2 + a2 - r2
�
.
Stelling 3 (hulpstelling)
Zij P een punt van de hoofdcirkel van een P-stelsel. Voor een cirkel (a) van het P-stelsel geldt dan:
   macht(P, (a)) = 2ax
waarbij x de afstand is van P tot de machtlijn van het P-stelsel.

Bewijs:

figuur 3 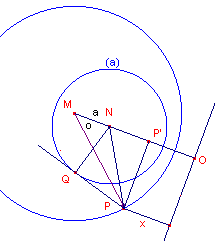sluitstel3.gif (2047 bytes) P' is de projectie van P op MO; Q is het raakpunt uit P aan cirkel (a)
Zij hoek(PMO) = M.
Nu is
macht(P, (a) = PQ2 = PN2 - r2 ......(3)
In driehoek PMN is volgens de cosinusregel:
   PN2 = R2 + a2 - 2aR.cosM ......(4)
zodat
   PQ2 = R2 + a2 - 2aR.cosM - r2
Volgens stelling 2 hebben we:
   PQ2 = 2ad -2aR.cosM = 2a(d - R.cosM) ......(5)
In driehoek PP'M is cosM = P'M/R waaruit P'M = RcosM

Met P'O = x en MO = d vinden we dan P'M = RcosM = d - x ......(6)
Uit (5) en (6) vinden we dan macht(P, (a)) = PQ2 = 2ax �

Stelling 4 begin pagina
A1A2 en B1B2 zijn koorden van de hoofdcirkel van een P-stelsel zo, dat A1B1 en A2B2 raken aan een cirkel (a) van het P-stelsel.
Zijn E en F raakpunten van A1A2 en B1B2 met coaxiaalcirkels ( a1 ) en ( a2 ), dan is
   a1 = a2.
(Stelling van Casey (1858) en Hart)

Klik hier Animatie voor een CabriJavapplet van Stelling 4.

Bewijs:

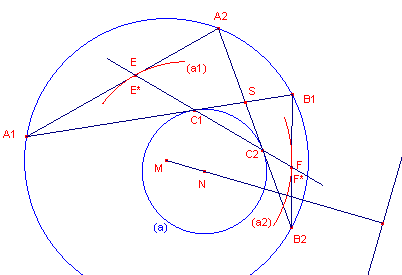figuur 4 sluitstel4.gif (3321 bytes) Zij xi de afstand van Ai tot de machtlijn van het P-stelsel; en zij yi de afstand van Bi tot die machtlijn (afstanden zijn niet getekend in figuur 4).
Zij verder E* = A1A2 /\ C1C2 en F* = B1B2 /\ C1C2, waarbij C1 en C2 de raakpunten zijn van opv. A1B1 en A2B2 aan (a).
Voorts zij S = A1B1 /\ A2B2.
Op driehoek A1A2S passen we de stelling van Menelaos toe met C2C1E* als transversaal. Dan is:
A1E*/E*A2 . A2C2/C2S . SC1/C1A1 = -1
Nu is SC1 = SC2 (raaklijnen uit S aan (a)), zodat
A1E*/E*A2 . A2C2/1 . (-1)/C1A1 = -1
waaruit volgt A1E*/E*A2 = C1A1/A2C2 ......(7)

Volgens stelling 3 is nu
   A1E = �(2a1x1)      B1F = �(2a2y1)
   A2E = �(2a1x2)      B2F = �(2a2y2)
Dus:
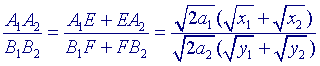sluitstel4a.gif (1919 bytes)......(8)
Verder geldt:
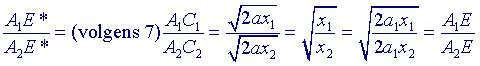
sluitstel4b.gif (2328 bytes)
De driehoeken A1SA2 en B2SB1 zijn gelijkvormig (hh; omtrekshoeken op dezelfde boog), zodat
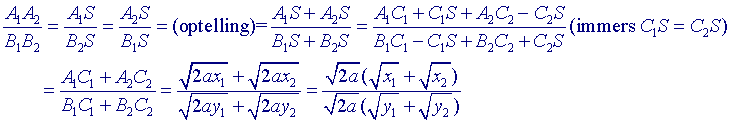sluitstel4c.gif (5291 bytes)......(9)

Vergelijking van (8) en (9) geeft
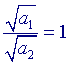
sluitstel4d.gif (587 bytes)
Dus a1 = a2. �

Opmerking
Bovenstaand bewijs is gebaseerd op het bewijs van Casey (1858).
Zie hiervoor ook [1], pag. 55.
[einde Opmerking]

De omgekeerde stelling van Casey en Hart (Stelling 4) luidt:

Stelling 5
Indien van coaxiaalcirkel (a1) de raakpunten E en F op de koorden A1A2 en B1B2 liggen, dan raken A1A2 en B1B2 eveneens aan een coaxiaalcirkel (a).

Het bewijs van stelling 5 laten we hier achterwege (het kan worden geleverd met een bewijs uit het ongerijmde).
We gebruiken de stelling in de volgende paragraaf.

3. Bewijs van de sluitingssteling begin pagina
We bewijzen nu stelling 1, de sluitingsstelling van Poncelet voor driehoeken.

figuur 5 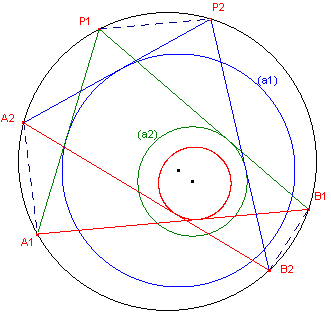sluitstel5.gif (4387 bytes) (1)...... P1A1 en P2A2 raken aan (a1).
Trek A1A2 en P1P2.
Deze lijnen raken volgens stelling 5 aan een (a3).
(2)...... P1B1 en P2B2 raken aan (a2).
Trek B1B2 en beschouw P1P2 en B1B2.
Deze lijnen raken volgens stelling 5 eveneens aan (a3).
(3)...... Uit (1) en (2) volgt nu:
A1A2 en B1B2 raken aan (a3)
Dus A1B1 en A2B2 raken aan een (a4) Deze cirkel is getekend in figuur 5. �

Gevolgen
[1]
Vallen (a1) en (a2) samen, dan is cirkel(M) de omgeschreven cirkel van de driehoek en cirkel (a1)=(a) de ingeschreven cirkel.
Zie de pagina "Om- en incirkel" voor een afleiding van nodige en voldoende voorwaarde voor sluiting.
Deze voorwaarde luidt: a2 = R2 - 2Rr.
In dit geval spreekt men wel van de "beperkte" Sluitingsstelling van Poncelet".
Zie voor een bewijs, gebaseerd op inversie, weer de pagina "Om- en incirkel".

Klik hier Animatie voor een CabriJavapplet ter illustratie.

[2]
Uitbreiding tot n-hoeken en kegelsneden
Stelling 1 is uit te breiden tot n-hoeken beschreven in een cirkel.
Bottema formuleert dit in [1] als volgt.

Stelling
Zijn twee cirkels C1 en C2 gegeven, kiest men op C1 een punt A1, zijn A1A2, A2A3, ... koorden van C1 die C2 raken, valt An+1 met A1 samen, zodat de alsus geconstrueerde gebroken lijn zich na n zijden sluit, dan heeft eveneens sluiting plaats, en wel eveneens na de nde zijde, als men begint in een willekeurig punt van C1.

Poncelet heeft de stelling bewezen voor kegelsneden in plaats van cirkels (1822). Een cirkel kan via een (centrale) projectie worden afgebeeld op een kegelsnede. Rakingseigenschappen zijn daarbij invariant.
Zie paragraaf 4 voor een projectief bewijs voor kegelsneden.

4. Projectief bewijs van de sluitingsstelling begin pagina

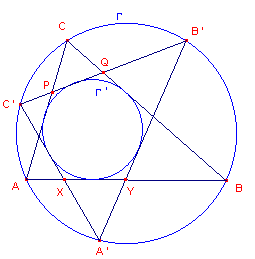figuur 6 sluitstel6.gif (2310 bytes) A, B, C, A', B', C' liggen op een kegelsnede (in figuur 6 moeten de cirkels G en G' worden opgevat als kegelsneden).
We kiezen twee punten, bijvoorbeeld A' en C als toppen van lijnenwaaiers.
Nu is er een projectieve afbeelding f van waaier A' op waaier C, en wel zo, dat
   fA'A=CA    fA'C'=CC'    fA'B'=CB'    fA'B=CB
f induceert een projectieve afbeelding g van AB op B'C', waarbij
   gA=P    gX=C'    gY=B'    gB=Q
De lijnen AP, XC', YB', BQ omhullen dus een kegelsnede die ook raakt aan de dragers AB en B'C' van deze puntenreeksen (immers G raakt tevens aan de voortbrengenden; de kegelsnede is nu vastgelegd door 5 lijnen).

Er is ��n en slechts ��n kegelsnede die raakt aan AP, XC', YB', BQ en AB, nl. de kegelsnede G'.
Dus B'C' raakt aan G'. �

Klik hier Animatie voor een CabriJavapplet van de sluitingsstelling voor kegelsneden..

5. Referenties begin pagina

[1]    O. BOTTEMA, Hoofdstukken uit de Elementaire Meetkunde, N.V. Servire, Den Haag, 1924
[2] A. HEIJTING, Projectieve meetkunde, P. Noordhoff, Groningen, 1963
[2]    P. WIJDENES, Vlakke meetkunde voor voortgezette studie, P. Noordhoff N.V., Groningen, 1964

begin pagina

[sluitstel.htm] laatste wijziging op: 19-06-02