Cirkelbundels

Cabri-werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht – Cirkelbundels

Vooraf
Cirkelbundels
   Opdracht 1 - Snijdende cirkels
   Opdracht 2 - Rakende cirkels
   Opdracht 3 - Niet-snijdende cirkels
   Opdracht 4
   Opdracht 5 - Toegift
Download

1. Vooraf
De benodigde voorkennis bij dit werkblad is (onder meer) het begrip "machtlijn"; zie hiervoor het Cabri-werkblad "Machtlijn van twee cirkels" en de webpagina "De macht van een punt tov. een cirkel".

figuur 1a	figuur 1b	figuur 1c

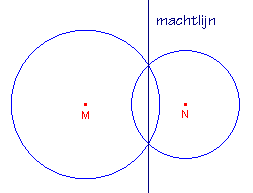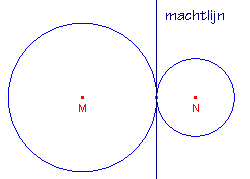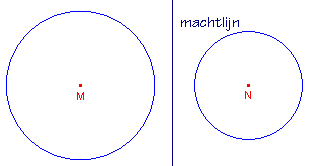We herhalen kort enkele zaken.

Elk tweetal cirkels (met uitzondering van twee verschillende concentrische cirkels) heeft een machtlijn (zie figuur 1).
De machtlijn staat loodrecht op de centraal van beide cirkels (de centraal is de verbindingslijn van de middelpunten).
Als we een punt R op de machtlijn van twee cirkels kiezen, dan zijn de lengtes van de raaklijnstukken uit dat punt aan die cirkels gelijk.
We kunnen de raaklijnstukken uit een punt aan een cirkel eenvoudig construeren (zie figuur 2); eventueel kan dit met een macro (zie daarvoor het Cabri-werkblad "De machtlijn van twee cirkels").

figuur 2

Bepaal het midden O van het lijnstuk PM.
Teken de cirkel (O, OP).
Bepaal de snijpunten van beide cirkels
Teken de lijnstukken PA en PB.
PA en PB zijn dan de gevraagde raaklijnstukken uit P aan de cirkel M.

Klik hier voor een CabriJavapplet bij deze constructie.

De machtlijn van snijdende en rakende cirkels kan eenvoudig worden bepaald (zie de figuren 1a en 1b hierboven).
Voor de constructie van de machtlijn van twee niet-snijdende cirkels gebruiken we een hulpcirkel die door de middelpunten van beide cirkels gaat (of een macro). Zie voor de constructie figuur 3.

figuur 3

Construeer de middelloodlijn van MN.
Kies het punt X daarop.
Teken de cirkel (X, XM).
Bepaal de snijpunten A₁, B₁ en A₂, B₂.
Teken de machtlijnen A₁B₁ en A₂B₂, met snijpunt R.
Teken de lijn door R evenwijdig aan de middelloodlijn.
Deze lijn is dan de machtlijn van beide cirkels.

Klik hier

voor een CabriJavapplet bij deze constructie.

2. Cirkelsbundels
Opdracht 1 – Snijdende cirkels

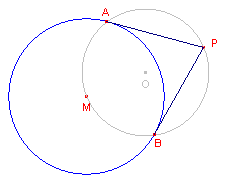a.	Teken twee, elkaar in de punten A en B snijdende cirkels (middelpunten M en N).
b.	Een derde cirkel gaat eveneens door de punten A en B. Op welke lijn ligt het middelpunt van deze derde cirkel? Teken een dergelijke cirkel.

De verzameling van alle
cirkels die door de punten A en B gaan, noemen we een cirkelbundel.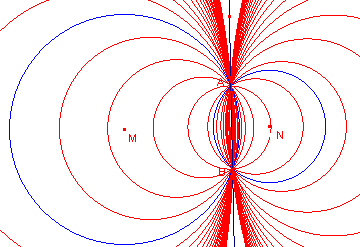
De beide cirkels die de machtlijn bepalen, noemen we wel de basiscirkels van de bundel.
In figuur 4 zijn aan aantal cirkels uit zo’n bundel getekend.

figuur 4 cirkb7.gif (5146 bytes)

c.	Wat is de meetkundige plaats van de middelpunten van de cirkels uit de bundel?
d.	Kies nu een punt R op de machtlijn van de bundel. Wat weet je van de raaklijnstukken uit R aan alle cirkels van de bundel. Wat is de meetkundige plaats van alle raakpunten van die raaklijnstukken aan alle exemplaren van de bundel? Maak die meetkundige plaats zichtbaar met de functie "Spoor aan/uit" uit het Extra-menu.
e.	Het construeren van een willekeurige cirkel uit de bundel (hier bepaald door twee snijdende cirkels) is eenvoudig. Schrijf kort op hoe je dat doet.
f.	Teken de cirkel met middelpunt R waarvan de straal gelijk is aan het raaklijnstuk uit R aan de cirkels van de bundel. Kies dan een punt X op deze cirkel, teken RX en de lijn die in R loodrecht staat op RX. Deze lijn snijdt de centraal in het punt Q. Teken de cirkel(Q, QX). Behoort deze cirkel tot de beschouwde cirkelbundel? Verklaar je antwoord.
g.	Heeft de bundel een kleinste cirkel? Zo ja, hoe groot is de straal van die cirkel?

Klik hier

voor een CabriJavapplet bij Opdracht 1.

Opdracht 2 – Rakende cirkels

a.	Teken op een nieuw Cabri-werkblad een punt M, een lijn door M en een cirkel met middelpunt M. Bepaal een snijpunt A van die lijn en de cirkel M (zie figuur 5a).
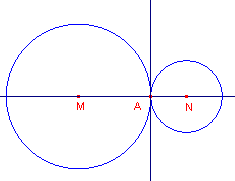
b.	Kies een punt N op de lijn en teken de cirkel met middelpunt N die door A gaat. Waarom raken beide cirkels elkaar? Teken ook de machtlijn van beide cirkels. Teken nu een derde cirkel uit de bundel.

figuur 5a	[figuur 5b]

c.	Voer nu de onderdelen c t/m g uit Opdracht 1 ook uit voor deze cirkelbundel.

Opdracht 3 – Niet-snijdende cirkels

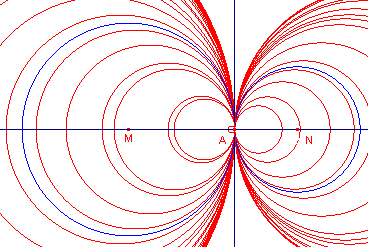
a.	Teken op een nieuw Cabri-werkblad twee elkaar niet-snijdende cirkels (teken ze buiten elkaar) en hun machtlijn. Op welke lijn ligt het middelpunt van een derde cirkel uit de bundel bepaald door de beide cirkels?
b.	Verklaar (bewijs) waarom zo’n derde cirkel de beide andere zeker niet snijdt.
c.	Kan je nu direct (zoals in Opdracht 1 en Opdracht 2) een derde exemplaar uit de bundel tekenen? Zo ja, beschrijf kort hoe je dat doet. Zo nee, waarom niet?

Opdracht 4

a.	Kies een punt R op de machtlijn van de bundel (uit Opdracht 3). Teken de cirkel met middelpunt R waarvan de straal gelijk is aan de lengte van het raaklijnstuk uit R aan de exemplaren van de bundel.
b.	Deze cirkel snijdt de centraal in de punten P₁ en P₂ (zie figuur 6). Verplaats nu het punt R over de machtlijn. Wat valt je op met betrekking tot de punten P₁ en P₂? Opmerking De punten P₁ en P₂ heten de punten van Poncelet van de bundel (naar Jean Victor Poncelet, 1788-1867, Frankrijk). Ze worden ook wel grenspunten van de bundel genoemd.

figuur 6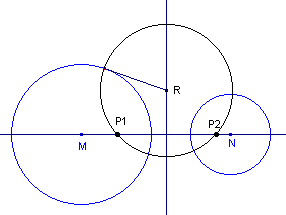

Klik hier

voor een CabriJavapplet bij figuur 6.

c.	Als je onderdeel c van Opdracht 3 nog eens bekijkt, kan je dan nu wel (als je dat eerder niet kon) een derde exemplaar uit de bundel construeren? Geef kort aan hoe je dat gedaan hebt.
d.	(facultatief) Probeer een bewijs te leveren voor de eigenschap van de punten P₁ en P₂. Als dat niet lukt, geef dan kort aan uit welke stappen dat bewijs volgens jou zou moeten zijn opgebouwd.
e.	Zijn er ook punten van Poncelet bij de bundel bepaald door twee snijdende cirkels? En bij de bundel bepaald door rakende cirkels?

Alle cirkels met middelpunt op de machtlijn die gaan door de punten P₁ en P₂, zijn exemplaren van een tweede cirkelbundel.

f.	Welke lijn is de machtlijn van die bundel? En welke lijn is de centraal?
g.	Bestaat een dergelijke cirkelbundel ook bij een bundel bepaald door snijdende cirkels? En bij een bundel bepaald door rakende cirkels. Zo ja, geef dan aan wat de centraal en de machtlijn is van die bundels.

figuur 7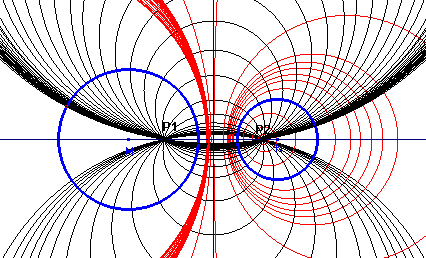

Opdracht 5 – Toegift

figuur 8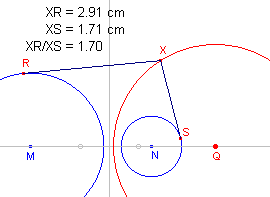

a.	Teken twee elkaar niet-snijdende basiscirkels van een cirkelbundel (middelpunten M en N) en de daarbij behorende machtlijn (zie figuur 8).
b.	Teken een derde cirkel uit de bundel (middelpunt Q), die niet gelegen is binnen ��n der basiscirkels. Kies een willekeurig punt X op cirkel Q. Teken de raaklijnstukken XR en XS uit X aan de beide basiscirkels.
c.	Bereken met de functie "Rekenmachine" de verhouding van de lengtes van XR en XS (dus XR/XS). Wat valt je op als je de positie van het punt X op de cirkel Q wijzigt?
d.	(facultatief) Bewijs?
e.	Als het punt X op de machtlijn van de bundel ligt, waaraan is XR/XS dan gelijk?

Klik hier voor een CabriJavapplet bij Opdracht 5.

3. Download
Dit werkblad is NIET MEER beschikbaar in PDF-formaat.
cirkb.pdf (ca. 376 Kb)
Een PDF-bestand kan met Acrobat^� Reader worden gelezen:

Enkele van de op deze pagina gebruikte figuren, inclusief die van alle applets, staan in een bestand.
Klik hier om dit bestand te downloaden (ca. 7Kb, ZIP-formaat).

[cirkb.htm] laatste wijziging op: 19-01-18