- Gergonne-punt
- Nagel-punt
- Symmediaan-punt (Lemoine-punt)
Meer over barycentrische co?rdinaten
Overzicht ][ Co?rdinatenstelsels | Meetkunde | Anal.Meetkunde
Overzicht ![]()
Bijzondere punten
- Gergonne-punt
- Nagel-punt
- Symmediaan-punt
(Lemoine-punt)
| Definitie Onder het spoor van een punt P verstaan we het snijpunt van een ceviaan door P met de overstaande zijde van de referentiedriehoek. |
Nb.
Een ceviaan van een driehoek is een lijn door een hoekpunt van die driehoek.
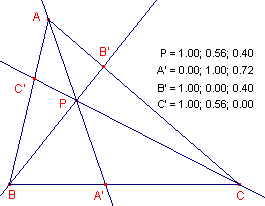 |
In de hiernaast staande figuur kunnen de co?rdinaten van de punten A',
B', C' ook worden weergeven als: A' = 0.00 : 0.56 : 0.40 (vermenigvuldiging met k = 0.56) B' = 1.00 : 0.00 : 0.40 C' = 1.00 : 0.56 : 0.00 |
Gevolg
Het Gergonne-punt van een driehoek ![]()
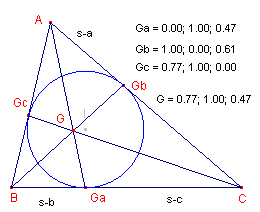 |
Nu geldt op BC: BGa = s-b, CGa = s-c Dus: Ga = 0 : s-c : s-b En ook: Gb = s-c : 0 : s-a Gc = s-b : s-a : 0 Of ook (na vermenigvuldiging met de juiste factoren): Ga = 0 : (s-a)(s-c) : (s-a)(s-b) Gb = (s-b)(s-c) : 0 : (s-a)(s-b) Gc = (s-b)(s-c) : (s-a)(s-c) : 0 |
Waarmee bewezen is dat de cevianen van de raakpunten van de incirkel (met de
overstaande zijde) concurrent zijn.
Dit punt is het Gergonne-punt G (ook wel aangegeven met Ge) van de
driehoek.
We hebben:
G = (s-b)(s-c) : (s-a)(s-c) : (s-a)(s-b)
of ook
G = 1/(s-a) : 1/(s-b) : 1/(s-c)
Het Nagel-punt van een driehoek ![]()
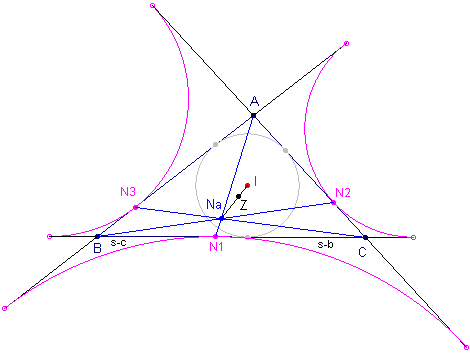 |
Op de zijde BC is BN1 = s-c, en CN1 = s-b, zodat N1 = 0 : s-b : s-c Analoog vinden we N2 = s-a : 0 : s-c N3 = s-a : s-b : 0 Volgens Stelling 1 zijn de lijnen AN1, BN2, CN3 concurrent in het punt Na = s-a : s-b : s-c Dit is dus het Nagel-punt van driehoek ABC. |
We hebben nu verder, op basis van de barycentrische eigenschappen:
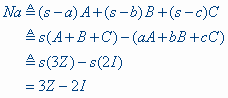
Of: 3Z = Na + 2I, of ook Z = 1/3 Na + 2/3 I
In bovenstaande afleiding betekent ![]() , dat het rechterlid genormaliseerd is.
, dat het rechterlid genormaliseerd is.
De laatste uitdrukking houdt in, dat het punt Z (het zwaartepunt van driehoek ABC) ligt op
de lijn INa, en wel zo, dat
NaZ : ZI = 2 : 1
Opmerking
Zie verder ook de pagina "Isotomische
verwantschap"
[einde Opmerking]
Symmediaan-punt (Lemoine-punt) ![]()
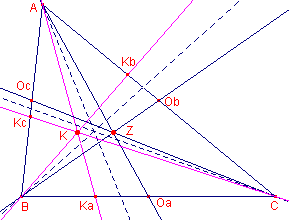 |
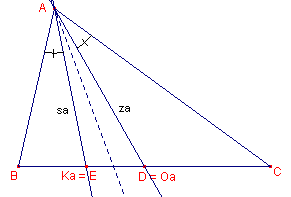 |
Zij E = Ka en D = Oa. Zij verder z = |AKa| en s = |AOa|.
Nu is:
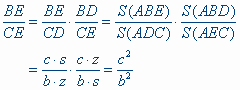
Zodat Ka = 0 : b2 : c2
Voor overeenkomstige punten Kb, Kc op de andere zijden vinden we dan
Kb = a2 : 0 : c2, Kc = a2 : b2
: 0
De lijnen AKa, BKb, CKc zijn dus concurrent in een punt K
met K = a2 : b2 : c2, het Lemoine-punt
van driehoek ABC.
Opmerkingen
Bewijs:
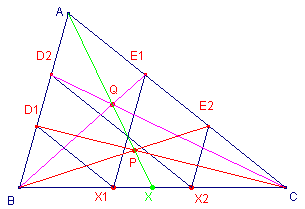 |
We beschouwen de cevianen BE1, CD2. Nu is, op basis van de constructie van de parallellogrammen: 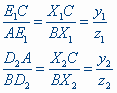 |
Uit de stelling van Ceva volgt nu (voor het punt P):
![]()
zodat
![]()
X is dus het punt met X = 0 : y1y2 : z1z2
Met eenzelfde berekening via het punt Q vinden we eveneens het punt X, waarmee het
gestelde is aangetoond. ?
| Definitie Voor de punten Pi = xi : yi : zi (i = 1,2) defini?ren we de sporen Pa, Pb, Pc met Pa = 0 : y1y2 : z1z2 Pb = x1x2 : 0 : z1z2 Pc = x1x2 : y1y2 : 0 |
Op basis van Stelling 1 gaan nu de cevianen APa, BPb, CPc door hetzelfde punt P, zodat we kunnen vastleggen:
| Definitie Onder het (barycentrisch) product P = P1 ? P2 met Pi = xi : yi : zi (i = 1,2) verstaan we het punt P = x1x2 : y1y2 : z1z2. Daarbij gebruiken we een vaste referentiedriehoek. |
| . |
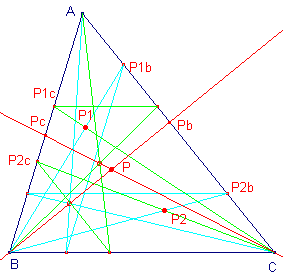 |
We kunnen het punt P, uitgaande van P1 en P2 met de sporen daarvan op twee zijden, construeren door gebruik te maken van Hulpstelling 2. |
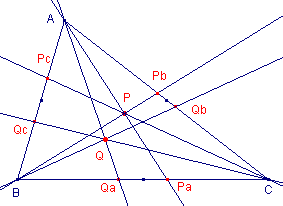
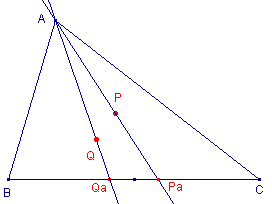
| Definitie De cevianen van de spiegelbeelden van de sporen van een punt P in de middens van de zijden zijn concurrent in een punt Q. Dit punt Q heet de isotomisch geconjugeerde van P. De isotomisch geconjugeerde van P geven we, in dit verband, vaak aan met P-1. |
| . |
| Stelling 3 Is P = x : y : z, met P niet op de zijden van de referentiedriehoek, dan is P-1 = 1/x : 1/y : 1/z. |
Bewijs:
Opmerking
Zie verder ook de pagina "Isotomische verwantschap"
[einde Opmerking]
| Definitie De spiegelbeelden van de cevianen van een punt P in de bissectrices van de referentiedriehoek zijn concurrent in een punt Q. Dit punt Q heet de isogonaal geconjugeerde van P. De isogonaal geconjugeerde van P geven we, in dit verband, vaak aan met P*. |
| . |
| Stelling 4 Is P = x : y : z, met P niet op de zijden van de referentiedriehoek, dan is de isogonaal geconjugeerde van P het punt P* = a2/x : b2/y : c2z. |
Bewijs:
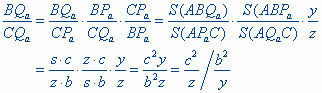
| Stelling 5 [1] De isogonaal geconjugeerde van Z = 1 : 1 : 1 is het Lemoine-punt van de driehoek: K = a2 : b2 : c2.: [2] Voor ieder punt P geldt P ? P* = K. |
Bewijs:
Klik hier ![]() voor een CabriJavapplet
bij Stelling 5.
voor een CabriJavapplet
bij Stelling 5.
| Stelling 6 Voor het incentrum I van een driehoek geldt: I2 = I ? I = K. |
Bewijs:
Opmerking
Zie ook de pagina "Isogonale verwantschap"
[einde Opmerking]
| Hulpstelling 7 Zij X een punt op het lijnstuk BC van driehoek ABC. De loodlijn in X op BC snijdt de cirkel met middellijn BC in X". De bissectrice van hoek BX"C snijdt BC in X'. Dan is X' ? X' = X. |
Bewijs:
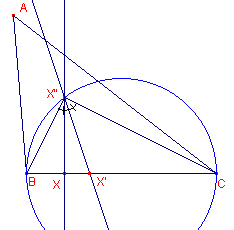 |
Volgens de bissectricestelling is BX' : CX' = BX" : CX". Zo dat Is nu X = 0 : b : c, dan is X = 0 : ? b : ? c, waaruit het gestelde volgt.? Opmerking |
Voorbeeld
Te construeren:
het punt P binnen een driehoek waarvoor de afstanden tot de zijden evenredig zijn
met de vierkantswortels van de lengten van die zijden.
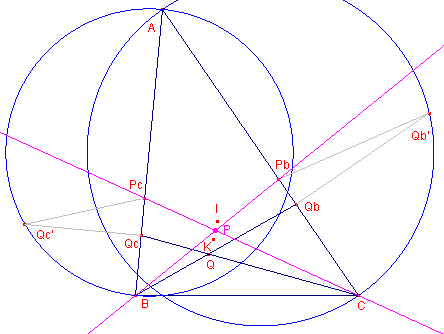
Als normaalco?rdinaten van P hebben we nu, op basis de voorwaarde waaraan P
moet voldoen:
Pnorm = ? a : ? b : ? c.
De barycentrische co?rdinaten van P zijn dan Pbary = a?
a : b? b : c? c
P is dus het vierkantswortelpunt van het punt Q = a3 : b3 : c3.
Maar voor Q geldt – en dat is onmiddellijk duidelijk –, dat Q = I ? K.
Waarmee de constructie kan worden uitgevoerd.
Opmerking
Het geconstrueerde punt P heet het vierkantswortelpunt van driehoek ABC.
In [Kimberling] wordt het dit punt aangegeven met X365.
[einde Opmerking]
[einde Voorbeeld]
6. Mittenpunkt
![]()
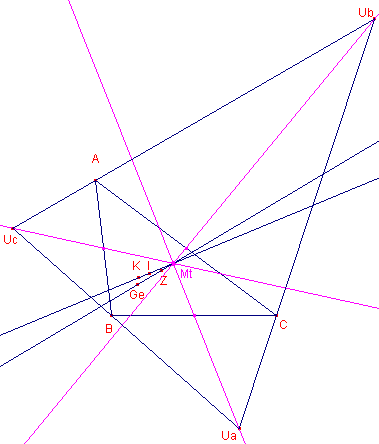
Het zogenoemde Mittenpunkt (Mt; Kimberling: X9) van een driehoek ABC wordt gedefinieerd als het
gemeenschappelijk punt van de verbindingslijnen van de uitcentra Ui van die
driehoek met het midden Oi van de bijbehorende zijde van de driehoek.
Opmerking
Zie ook de pagina "Uitcirkels"
[einde Opmerking
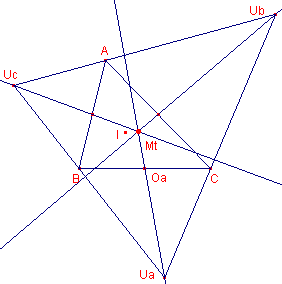 |
We weten Ibary = a : b : c, zodat Ua = -a : b : c. Voor de vergelijking van de lijn UaOa die gaat door de punten Ua en Oa = 0 : 1 : 1 vinden we (na enig rekenwerk): UaOa: (b-c)x + ay – az =0 Zo ook is de vergelijking van UbOb: UbOb: bx + (a-c)y – bz =0 Voor het snijpunt Mt van deze lijnen vinden we dan Mt = a(-a+b+c) : b(a-b+c) : c(a+b-c) of ook Mt = a(s-a) : b(s-b) : c(s-c) Eenvoudig is na te gaan, dat dit punt ook op de lijn UcOc met vergelijking cx – cy + (a-b)z =0 ligt. |
We hebben gevonden dat Mt bary = a(s-a) : b(s-b) : c(s-c)
We zien hieruit, dat Mt = I ? Na, waarin Na het Nagel-punt is
van de driehoek.
Nu is
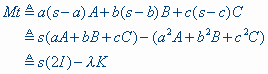
zodat
![]()
waaruit volgt, dat het Mt collineair is met het incentrum I (Kimberling: X1) en het Lemoine-punt K (Kimberling: X6). ?
| Hulpstelling 8 |
Bewijs:
 |
Schrijven we Zodat 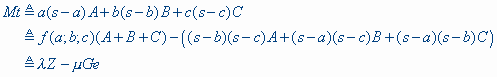 We zien hieruit, dat het Mittenpunkt Mt ook collineair is met het zwaartepunt Z (Kimberling: X2) en het Gergonne-punt Ge (Kimberling: X7). ? |
[einde Gevolg]
| [1] | O. BOTTEMA: Hoofdstukken uit de Elementaire Meetkunde, Epsilon (Utrecht, 1997) | |
| [2] | CLARK KIMBERLING: Triangle Centers and Central Triangles, Utilitas Mathematical Publishing Inc. (Winnipeg, Canada, 1998) | |
| [3] | CLARK KIMBERLING: Encyclopedia of Triangle Centers - ETC (website). | |
| [4] | PAUL YIU: The uses of homogeneous barycentric coordinates in plane euclidean geometry, in: International Journal of Mathematical Education in Science and Technology, 31 (2000) 569-578 |
8. Download ![]()
De in de CabriJavapplets gebruikte figuren kunnen in ?en bestand via deze website worden
gedownload.
Klik hier om het downloaden te starten
(ZIP-bestand; ca. 4kB).