Isotomische verwantschap bij een driehoek, ellipsen van Steiner
 |
N.b.
|
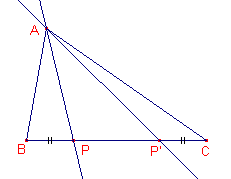
| Gevolg De zwaartelijnen van een driehoek zijn isotomisch verwant met zichzelf. |
| . |
| Stelling 1 Zijn drie lijnen door opvolgend A, B, C (hoekpunten van een driehoek) concurrent, dan zijn de isotomisch verwanten van die lijnen (tov. de driehoek) eveneens concurrent. |
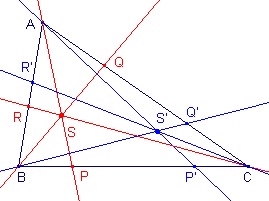 |
Snijden de lijnen AP, BQ en CR elkaar in het punt S, dan geldt volgens de
stelling van Ceva: Vanwege de isotomie hebben we: AR' = - BR, BR' = - AR, …, zodat uit deze betrekking volgt: Volgens de (omgekeerde) stelling van Ceva zijn de lijnen AP', BQ' en CR' nu concurrent. � |
Opmerking
| Gevolg Het zwaartepunt van een driehoek is isotomisch verwant met zichzelf. |
| . |
| Stelling 2 De hoekpunten van de driehoek gevormd door de lijnen door de hoekpunten die evenwijdig zijn met de overstaande zijde, zijn isotomisch verwant met zichzelf. |
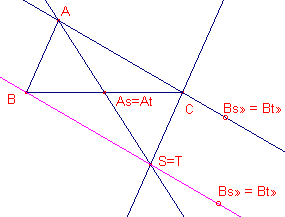 |
Zij S het hoekpunt gevormd door de lijnen evenwijdig met AB en AC. En zij
T het met S verwante punt. Nu is As = At (op BC; immers As is het midden van BC). BS snijdt AC in Bs. Bs is dus het oneigenlijk punt van AC en BS (= Bs�; in nevenstaande figuur aangegeven met Bs�). Het punt Bt� valt daarmee samen. De lijn BBt� snijdt de lijn AAt in het punt T, dat dus samenvalt met S. � Klik hier |
| . |
| Stelling 3 Snijdt een transversaal de zijden van driehoek ABC in de punten P, Q, R dan zijn de isotomisch verwante punten P', Q', R' (tov. de driehoek ABC) collineair. |
Bewijs:
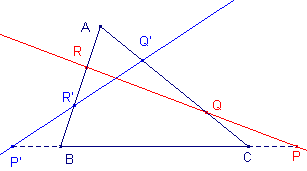 |
Volgens de stelling van Menelaos is nu: Voor de isotomisch verwante punten P', Q', R' van P, Q, R geldt nu: PB = - P'C, PC = -P'B, …, zodat waaruit weer volgens de omgekeerde stelling van Menelaos volgt dat P', Q, R' collineair zijn. � |
| . |
| Stelling 4 Het Gergonne-punt en het Nagel-punt van een driehoek zijn isotomisch verwant. |
Zie ook de pagina "Barycentrische co�rdinaten"
Bewijs:
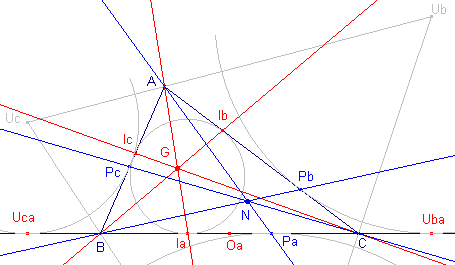 |
G is het Gergonne-punt van driehoek ABC; N is het Nagel-punt. Oa is het midden van BC. De punten Ia, Ib, Ic zijn de raakpunten van de incirkel met de zijden; de punten Pa, Pb, Pc zijn de raakpunten van de uitcirkels met de zijden. Uba en Uca zijn de andere raakpunten op de zijde BC. We dienen nu aan te tonen, dat OaIa = OaPa. Volgens
een bekende eigenschap van de raaklijnstukken aan de incirkel en aan de uitcirkels is nu: |
| . |
| Stelling 5 Twee punten die isogonaal verwant zijn tov. een gelijkzijdige driehoek, zijn isotomisch verwant tov. die driehoek (en omgekeerd). |
Zie ook de pagina "Barycentrische co�rdinaten"
Bewijs:
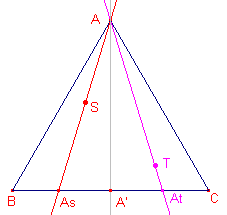 |
Zijn S en T twee isogonaal verwante punten;
dwz. dat de verbindingslijnen van die punten met een hoekpunt (bijvoorbeeld het punt A)
elkaars beeld zijn bij een spiegeling in de bissectrice van de hoek. In de figuur is dus AAt het spiegelbeeld van AAs in AA' (die de middelloodlijn is van BC). Hieruit volgt eenvoudig, dat A'As = A'At. � |
2. Ellipsen van
Steiner ![]()
Er is een ellips die door de middens van de zijden van een driehoek
gaat en in die punten aan de zijden van die driehoek raakt (ingeschreven ellips).
Immers, een ellips is bepaald door vijf elementen. We kunnen daarvoor drie punten en twee
raaklijnen gebruiken. We kiezen twee middens van de zijden en de zijden zelf, en het
midden van de derde zijde.
Volgens de stelling van Brianchon is dan de derde zijde
eveneens raaklijn.
Deze ingeschreven ellips heet de (eerste) Steiner-ellips van de driehoek; het middelpunt van de ellips is het zwaartepunt Z van de driehoek.
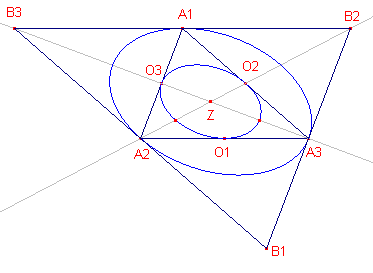 |
Uit deze ellips kunnen we een tweede laten ontstaan door
vermenigvuldiging met factor –2 tov. het punt Z. Deze ellips (een omgeschrevn ellips) is de (tweede) Steiner-ellips van de driehoek. De hoekpunten van de driehoek liggen op de ellips en de raaklijnen in die hoekpunten zijn evenwijdig met de overstaande zijden. |
Voor die tweede Steiner-ellips geldt nu:
| Stelling 6 De isotomisch verwante rechten van de verbindingsrechten van de punten van de tweede Steiner-ellips met de hoekpunten van de driehoek zijn evenwijdig. |
Bewijs:
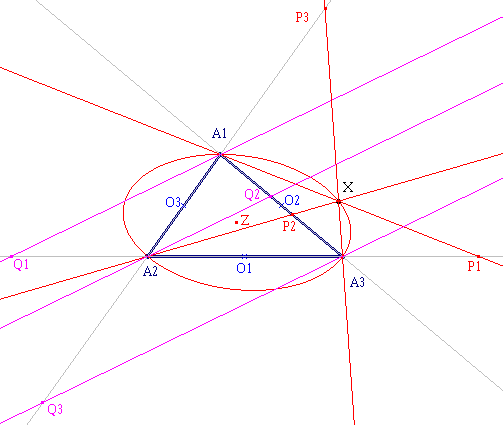 |
In nevenstaande figuur willen we nu aantonen, dat de lijnen A1Q1,
A2Q2, A3Q3 evenwijdig zijn. De punten Q1, Q2, Q3 zijn de isotomisch verwanten van de punten P1, P2, P3. O1, O2, O3 zijn de middens van de zijden van driehoek ABC. Klik hier We geven het bewijs van de stelling met behulp van een affiene afbeelding. |
We gaan nu uit van een gelijkzijdige driehoek ABC.
We kiezen een affiniteitsas m en bepalen de afbeelding verder met behulp van het
punt A1, dat het beeld is van A.
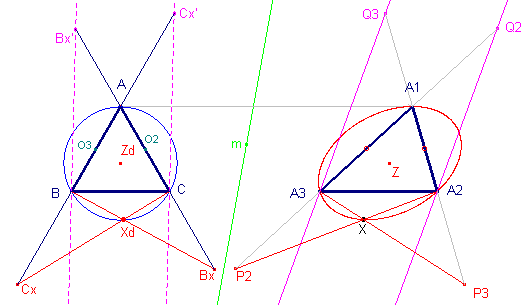 |
Volgens Stelling 5 zijn punten die isotomisch verwant (tov. driehoek ABC) zijn nu ook isogonaal verwant (tov. driehoek ABC). Het beeld van de
omcirkel bij een isogonale afbeelding is de oneigenlijke rechte (zie Stelling 3c op de pagina "Isogonale
verwantschap"). X is het affiene beeld van Xd. |
De affiene beelden van BBx' en CCx' zijn nu A2Q2 en
A3Q3.
Deze laatste lijnen zijn dus eveneens evenwijdig. �
Klik hier ![]() voor een CabriJavapplet
bij de laatste figuur.
voor een CabriJavapplet
bij de laatste figuur.
De figuren gebruikt in de CabriJavapplets kunnen in een bestand via deze websiet worden
gedownload. In het bestand zijn ook enkele andere figuren betrekking hebbend op deze
pagina opgenomen.
Klik hier om het downloaden te starten
(ZIP-bestand; ca. 10kB).