Overzicht ][ Lemoine en Kiepert | Grebe's constructie | Meetkunde
1. Loodrechte
stand en concurrentie ![]()
| Stelling 1 Op de zijden van driehoek ABC zijn uitwendig vierkanten beschreven (zie figuur 1). De lijnenparen (ABc , BAc ), (BCa , CBa ), (CAb , ACb ) staan loodrecht op elkaar. (Stelling van Vecten, 1817) |
| . |
| figuur 1 | 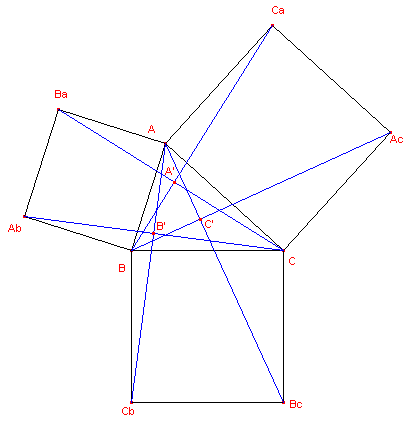 |
Bewijs: We bekijken de rotatie met centrum A over een hoek van 90� (positief). A wordt afgebeeld op A; Ba wordt afgebeeld op B; C wordt afgebeeld op Ca. Uit de laatste twee regels volgt dan dat CBa wordt afgebeeld op CaB. Dus staat CBa loodrecht op CaB. Op dezelfde manier bewijzen we de beide andere eigenschappen. � Zie in dit verband ook de pagina "Constructie van Grebe". |
| . Gevolg |
| figuur 2 | 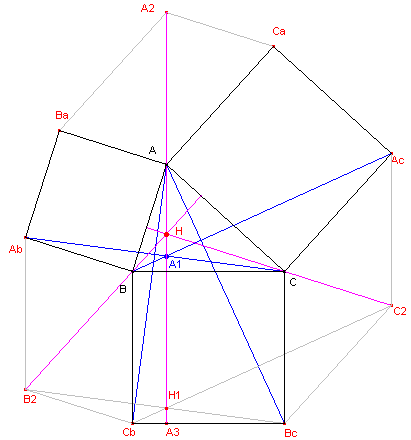 |
Bewijs: |
Tussenresultaat
We bewijzen nu, dat het snijpunt A1 van de lijnen BAc
en CAb op de lijn AA3 ligt.
We bekijken daartoe de translatie T over de vector BcC.
We hebben:
T(CbC2) = BAc
T(B2Bc) = AbC
en
T(AA3) valt langs AA3.
H1 is snijpunt van CbC2, B2Bc
en AA3. Het beeld van H1 ligt dus op
de beelden van deze drie lijnen. Dus:
T(H1) = A1.
[einde Tussenresultaat; zie verder ook onderstaande Opmerking mbt. de Stelling
van Pythagoras]
Zie nu verder figuur 3.
| figuur 3 | 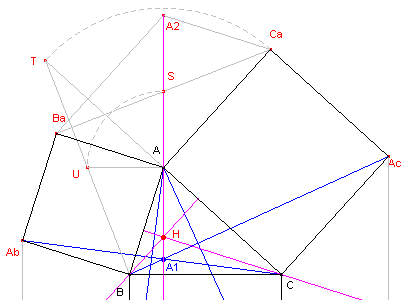 (dit is een deel van figuur 2) |
We zullen bewijzen, dat AA2 loodrecht staat op
BC. Bekijken we nu de rotatie R met centrum A en hoek 90� (positief). Nu is: R(Ba) = B R(Ca) = T zodat R(BaCa) = BT Het punt T ligt op het verlengde van CA. Zij S het midden van BaCa. Het beeld U = R(S) is dus het midden van BT. UA is middenparallel van driehoek BCT. UA is evenwijdig met BC. Maar, AA2 staat loodrecht op UA, dus AA2 staat loodrecht op BC. AA2 is dus hoogtelijn uit A van driehoek ABC. |
Op dezelfde manier bewijzen we, dat BB2 en CC2
hoogtelijnen zijn van driehoek ABC (zie figuur 2).
De lijnen AA2, BB2 en CC2
zijn dus concurrent in het punt H. �
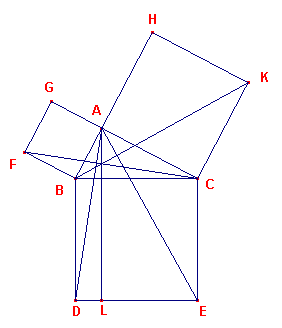 |
Het bovenstaande tussenresultaat voor een in A
rechthoekige driehoek laat zien dat de hulplijnen in het bewijs van Euclides
van de Stelling van Pythagoras (zie de
figuur hiernaast) inderdaad concurrent zijn (hier in het punt A1). Dit resultaat staat bekend als de Stelling van Heron. |
[einde Opmerking]
| Stelling 3a AbBa2 + BcCb2 + CaAc2 = 3 (AB2 + BC2 + CA2) (zie figuur 4) |
| . |
| figuur 4 | 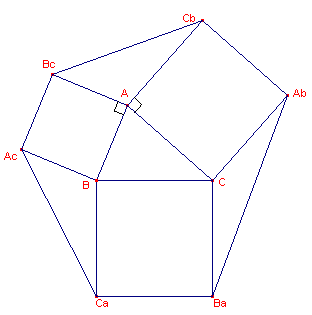 |
Bewijs: In driehoek ACbBc geldt: BcCb2 = BcA2 + CbA2 - 2 BcA . CbA cos BcACb Verder is hoek(BcACb) = pi - hoek(ABC), zodat BcCb2 = AB2 + AC2 + 2 AB.AC cos A In driehoek ABC hebben we BC2 = AB2 + AC2 - 2 AB.AC cos A, zodat BcCb2 = 2 AB2 + 2 AC2 - BC2 ......(1) Evenzo: AbBa2 = 2 BC2 + 2 AC2 - AB2 ......(2) en AcCa2 = 2 AB2 + 2 BC2 - AC2 ......(3) Optelling van (1), (2) en (3) geeft AbBa2 + BcCb2 + CaAc2 = 3 (AB2 + BC2 + CA2) � |
| Stelling 3b.
De oppervlaktes van de drie "verbindingsdriehoeken" zijn gelijk. |
Bewijs: zie figuur 4
Zij OX de oppervlakte van de "verbindingsdriehoek" bij
het hoekpunt X van driehoek ABC (bijv. OA = oppervlakte van ACbBc).
Voor de driehoek bij A geldt OA=�bc . sinA
Voor die bij B en C geldt OB=�ac . sinB
en OC=�ab . sinC
Zodat aOA/sinA = �abc, bOB/sinB =
�abc, cOC/sinC = �abc
Wegens a/sinA = b/sinB = c/sinC (sinusregel) vinden we dus
OA = OB = OC
�
| Stelling 4a De verbindingslijnen van de middelpunten van de vierkanten op de zijden met de tegenoverliggende hoekpunten zijn concurrent (dit punt heet het (eerste) punt van Vecten). |
Bewijs: zie figuur 5
| figuur 5 | 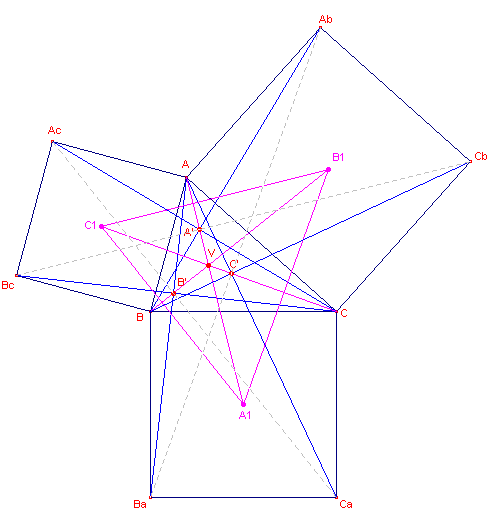 |
We willen dus aantonen, dat AA1, BB1,
CC1 concurrent zijn in het punt V. Uit stelling
1 weten we: |
A'A1 is dus ook bissectrice van hoek BA'C. Dus de lijnen AA' en A'A1 liggen in elkaars verlengde.
In driehoek ABcCb is C1B1
middenparallel. Zodat C1B1 // BcCb.
De lijn AA1 staat loodrecht op BcCb
en dus ook AA1 loodrecht op C1B1.
AA1 dus hoogtelijn van driehoek A1B1C1.
Analoog zijn ook BB1 en CC1
hoogtelijnen van die driehoek.
AA1, BB1, CC1
zijn dus concurrent in het hoogtepunt V (het punt van Vecten) van driehoek A1B1C1.
�
Opmerking
Het eerste punt van Vecten kan natuurlijk ook gevonden worden door op de zijden van
driehoek ABC rechthoekige gelijkbenige driehoeken AC1B, BA1C,
CB1A te construeren.
Stelling 4 kan dus ook geformuleerd worden als
| Stelling 4b De verbindingslijnen van de toppen van die driehoeken met de overeenkomstige hoekpunten van de driehoek zijn dus concurrent. |
Zie de pagina "Probleem van Lemoine en de Stelling van
Kiepert".
Op deze pagina wordt het (eerste en het tweede) punt van Vecten behandeld
in samenhang met de Kiepert-hyperbool van de driehoek.
Op de pagina "De stelling van Van Aubel" wordt in Stelling 3 een ander bewijs voor de concurrentie van de lijnen in het punt van Vecten gegeven.
[einde Opmerking]
3. Tweede punt
van Vecten ![]()
Ook indien de vierkanten binnenwaarts worden beschreven op de de zijden, gaan de bedoelde
verbindingslijnen door ��n punt.
Dit punt wordt het Tweede punt van Vecten genoemd (het punt V in figuur 6).
| figuur 6 | 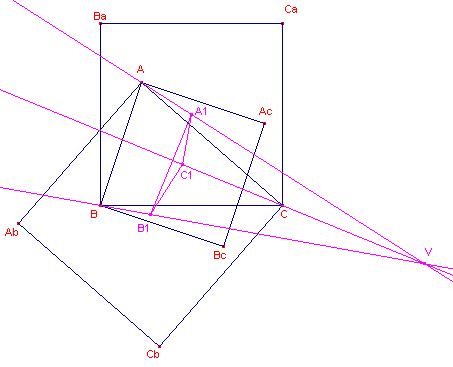 |
Het bewijs verloopt analoog aan dat van stelling 4. |