Complex bewijzen - 5 (Over bissectrices)
Overzicht ][ Complexe vlak | Meetkunde
Naar pagina 1 | Naar pagina 2 | Naar pagina 3 | Naar pagina 4
12. Het midden van een
cirkelboog ![]()
We kiezen de punten A en B (affixen a en b) op de eenheidscirkel.
De punten met affixen a2 en b2 liggen
dan ook op die cirkel.
De beide middens M van de bogen tussen a2 en b2
geldt dan m = ab en m = -ab.
Echter, de plaats van bijvoorbeeld m = ab op de kleinste of op de grootste boog ligt niet
vast, immers de berekening verloopt via de argumenten modulo p.
Klik hier ![]() voor een CabriJavapplet
waarin dat wordt ge�llustreerd.
voor een CabriJavapplet
waarin dat wordt ge�llustreerd.
13. Bissectrices van
een driehoek ![]()
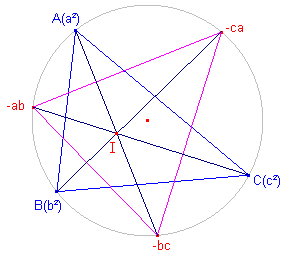
We kiezen de punten A, B, C op de eenheidscirkel (affixen a2, b2,
c2).
We tekenen de bissectrices van de hoeken die elk gaan door het midden van die boog tussen
de beide andere hoekpunten die het betreffende hoekpunt niet bevat.
We kiezen de ligging zo, dat de snijpunten van de bissectrices met de eenheidscirkel
opvolgend zijn:
-bc, -ca, -ab.
Voor de vergelijking van de bissectrice van A vinden we dan (zie
paragraaf 6.5):
x - a2bcx_ = a2 - bc
......(1)
Voor die van de bissectrice van B vinden we analoog:
x - b2cax_ = b2 - ca
......(2)
Oplossing van het stelsel (1) en (2) naar x geeft:
(b - a)x = a2b - b2c
- ab2 + ac2 ......(3)
Duidelijk is dat het rechter lid van (3) deelbaar is door (b - a), waardoor
x = -ab - bc - ca
Deze oplossing is symmetrisch.
Het snijpunt, dat we aangeven met I, ligt dus ook op de derde bissectrice van de driehoek.�
| Stelling 12 De (binnen)bissectrices van driehoek ABC zijn concurrent in I. Het punt I is het middelpunt van de incirkel van de driehoek. |
| . |
 |
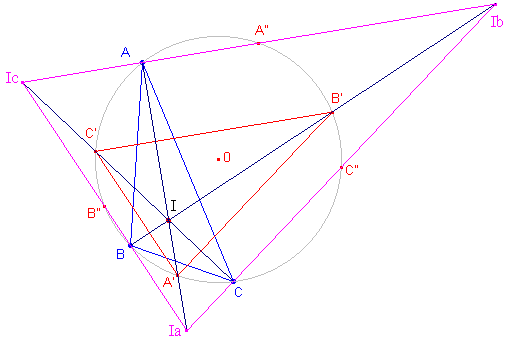
Gevolg Bekijken we de oplossing x = -ab - bc - ca dan zien we dat I tevens het hoogtepunt is van de driehoek met als hoekpunten de "voetpunten" van de bissectrices op de omcirkel (zie Samenvatting na Stelling 11; en zie ook de punten A',B',C' in onderstaande figuur). De punten bc, ca, ab zijn de tegenpunten van deze
hoekpunten op de eenheidscirkel (in onderstaande figuur aangegeven met A", B",
C"). |
 |
Voor de punten A", B", C" hebben we: A": z = bc B": z = ca C": z = ab Een vergelijking van de lijn BB" is nu: x + b2cax_ = b2 + ca ......(4) We hadden reeds: De vergelijking van CC": |
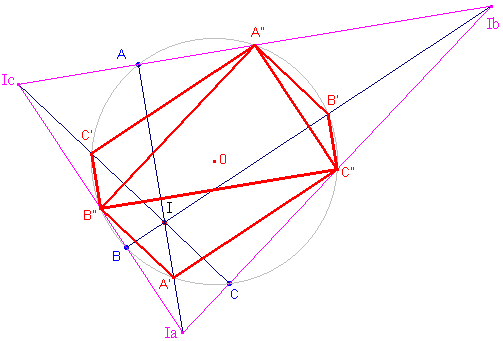 |
We vinden: Ia: z = -bc + ca + ab Evenzo: Ib: z = -ca + ab + bc Ic: z = -ab + bc + ca Opmerking |
14. Straal van de
incirkel en van de uitcirkels (Stelling van Feuerbach) ![]()
14.1 Incirkel
14.2 Uitcirkels
Bij berekeningen komen de volgende "afkortingen" soms goed van pas:
s = a + b + c
t = ab + bc + ca
u = abc
14.1. Incirkel ![]()
BC: x + b2c2x_ = b2
+ c2 ......(6)
De loodlijn hierop door I (z = - t) : x - b2c2x_
= -t + b2c2t_ ......(7)
Nu is t_ = 1/ab + 1/bc + 1/ca = c/u + a/u + b/u = s/u = s/abc
Zodat (7) overgaat in
x - b2c2x_ = -t +
bcs/a ......(8)
Oplossing van (6) en (8) naar x geeft de affix van het raakpunt van de incirkel op BC:
z = �(b2 + c2 - t
+bcs/a)
Voor de straal r van de incirkel vinden we dan:
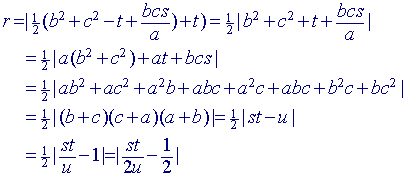 ......(9)
......(9)
Nb. Hierbij hebben we gebruik gemaakt van het feit dat |u| = 1.
Zij nu N het middelpunt van de negenpuntscirkel.
Dan is:
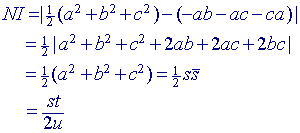 ......(10)
......(10)
Bij de laatste afleiding is gebruik gemaakt van s_ = 1/a + 1/b + 1/c = t/u.
Voor d = NI vinden we uit (9) en (10):![]()
Nu is d < 1/2, zodat
r = 1/2 - d geeft d = 1/2
- r
�
We hebben nu bewezen:
Klik hier voor een synthetische behandeling van de Stelling van Feuerbach.
[bissec.htm] laatste wijziging op: 16-05-02