Complexe getallen en meetkundige bewijzen

Overzicht  ][ Meetkunde | Complexe vlak

Zie voor de basisbegrippen de pagina: "Afbeeldingen van het complexe vlak [1]", 1. Inleiding.
Zie ook de pagina "Afbeeldingen van het complexe vlak [3] (ivm. "oneindig" en dubbelverhouding).

0. Overzicht terug

op deze pagina (1)
  1. Inleiding
  2. Driehoeksongelijkheid
  3. Stelling van Ptolemaeus-Euler
pagina 2
  1. Gelijkvormige driehoeken
  2. Drie punten op een lijn
  3. Vergelijking van een lijn / loodrechte stand
pagina 3
  1. Middelloodlijnen van een driehoek
  2. Stelling van Napoleon
  3. Stelling(en) van Clifford cabrisignal.gif (160 bytes)
pagina 4
  1. (Generalisering van de) Negenpuntscirkel cabrisignal.gif (160 bytes)
  2. Referenties
pagina 5
  1. Het midden van een cirkelboog cabrisignal.gif (160 bytes)
  2. Bissectrices van een driehoek
  3. Straal van de incirkel en van de uitcirkels

1. Inleiding terug
In het onderstaande maken we gebruik van complexe getallen bij het bewijzen van meetkundige eigenschappen van figuren.

Afspraken
[1] In het euclidische vlak is een orthonormaal assenstelsel gedefinieerd, met centrum O. De x-as noemen we in hetgeen volgt de re�le as; de y-as heet de imaginaire as.
[2] Aan een (euclidisch) punt A(a1, a2) voegen het complexe getal a = a1 + a2i toe, de affix van A.

2. Driehoeksongelijkheid terug

Definities
[1] De modulus van een complex getal a = (a1, a2): bewijsf1.gif (808 bytes)
[2] Re(a) = a1; Im(a) = a2

Opmerking: Voor de geconjugeerde (a1, -a2) van a schrijven we op deze website vaak a_.

Gevolg
Re(a) = (a + a_)/2
Re(ab_) = (ab_ + a_b)/2, zodat 2Re(ab_) = ab_ + a_b
[einde Gevolg]

Stelling 1 (Driehoeksongelijkheid)
Voor willekeurige complexe a en b geldt: bewijsf2.gif (783 bytes)
Het gelijkteken in het tweede deel geldt als a/b > 0.

Bewijs:
Tweede deel:
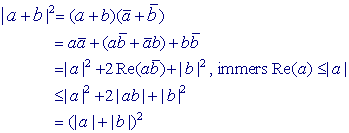
bewijsf3.gif (2491 bytes)
    |a + b| en |a| + |b| zijn beide positief, zodat
    |a + b| � |a| + |b|

Eerste deel:
    a = (a + b) - b
    |a| = |(a + b) + (-b)| � |a + b| + |-b| = |a + b| + |b|
Dus
    |a| - |b| � |a + b|
Maar door rolwisseling van a en b blijkt ook |b| - |a| � |a| + |b|, zodat
    | |a| - |b| | � |a + b|

Interessant is te weten wanneer in het tweede deel het gelijkteken geldt.
Triviaal is dit, als a = 0 of b = 0.
We onderstellen dus ab � 0.
In bovenstaand bewijs zien we dat het gelijkteken geldt als Re(ab_) = |ab|
Voor een complex getal p dat voldoet aan Re(p) = |p|, geldt p is re�el en p is niet-negatief.
De gelijkheid geldt dus als ab_ � 0.
Deling door |b|2 geeft dan a/b > 0.
a is dus een positief veelvoud van b. �

3. Stelling van Ptolemaeus-Euler terug

Lemma
Voor complexe getallen a, b, c, d geldt
(a - b)(c - d) + (a - d)(b - c) = (a - c)(b - d)

Bewijs: door uitschrijven.  �

Stelling 2 (Ptolemaeus-Euler)
Voor vier punten A, B, C, D in een vlak geldt: AB.CD + BC.DA � AC.BD
De gelijkheid geldt DESDA de punten op een cirkel (of op een rechte lijn) liggen.

Opmerking
De gelijkheid is ontdekt door Ptolemaeus (100-168). Zie ook de pagina: Stelling van Ptolemaeus en de sinusregel.
De algemene formulering is ontdekt door Leonard Euler (1707-1783).
[einde Opmerking]

Bewijs:
Zij a, b, c, d de affixen van A, B, C, D.
Volgens het Lemma en de driehoeksongelijkheid hebben we nu:
|(a - b)(c - d)| + |(a - d)(b - c)|  �  |(a - c)(b - d)|
|a - b| . |c - d| + |a - d| . |b - c|  �  |a - c| . |b - d|
Het gelijkteken geldt als (a-b)(c-d) / (a-d)(b-c) een positief re�el getal is (zie Driehoeksongelijkheid).
Dan is ( (a-b)/(a-d) ) / ( (c-b)/(c-d) ) een negatief getal.
Dus arg( (a-b)/(a-d) ) / ( (c-b)/(c-d) ) � p (mod 2p)
Zodat ook arg(a-b)/(a-d) - arg(c-b)/c-d) � p (mod 2p), immers arg(p/q) = arg(p) - arg(q).
Uit dit laatste volgt, dat a, b, c, d op een cirkel liggen (in de gegeven alfabetische volgorde). �

Opmerking
De uitdrukking ( (a-c)/(a-d) ) / ( (b-c)/(b-d) ) is de dubbelverhouding van a,b,c,d.
Deze wordt geschreven als: (a,b,c,d).
[einde Opmerking]

Gevolg

Stelling 3
(a,b,c,d)  is re�el DESDA a,b,c,d liggen op een cirkel.

Opmerkingen
[1]
Deze stelling is op de pagina "Afbeeldingen van het complexe vlak [3]" eveneens voor complexen bewezen.
Klik hier voor dat bewijs.
[2]
Vormen A, B, C, D een rechthoek, dan volgt uit de stelling van Ptolemaeus:
   AB2 + BC2 = AC2 (Stelling van Pythagoras)
[einde Opmerkingen]

� Klik hier voor de volgende pagina
begin pagina

[bewijs1.htm] laatste wijziging op: 09-06-02