Overzicht ][ Rotaties | Meetkunde
Zie ook de pagina "Bewegingen".
| Definitie Een draaivermenigvuldiging is de meetkundige afbeelding die bestaat uit een vermenigvuldiging gevolgd door een rotatie (zie figuur 1a). We geven een dergelijke afbeelding aan met D(O, h, k), of ook wel (O, h, k) waarbij O het centrum is van de rotatie, h de rotatiehoek en k de vermenigvuldigingsfactor (hierbij is, indien niet anders vermeld, k > 0). |
| figuur 1a | 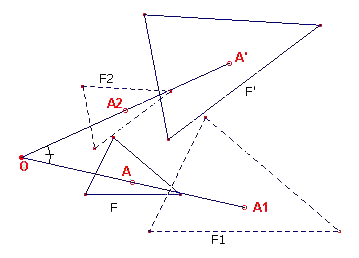 |
Eenvoudig is aan te tonen, dat D = RoV = VoR,
waarbij R de rotatie en V de vermenigvuldiging is. [einde Opmerking] |
1.2. Constructie van het
centrum ![]()
Een draaivermenigvuldiging is ook vastgelegd door het geven van twee punten en hun
beeldpunten.
Daaruit kan dan het centrum, de factor en de rotatiehoek worden bepaald.
| figuur 1b | 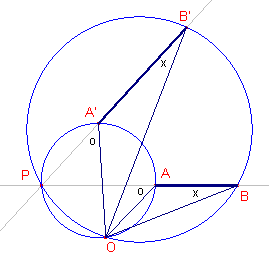 |
In de figuur hiernaast is D(A)
= A' en D(B) = B', waarbij D een draaivermenigvuldiging is. P is het snijpunt van de dragers van AB en A'B'. Voorts zijn getekend de omcirkels van de driehoeken PAA' en PBB'. Deze snijden elkaar (naast P) in het punt O. Nu is O het centrum van de draaivermenigvuldiging. Daarvoor is het nodig aan te tonen, dat de driehoeken OAB en OA'B" gelijkvormig zijn. In de hiernaast staande figuur is dan: � OAP = � OA'P (omtrekshoeken op dezelfde boog van cirkel PAA'), waaruit we
vinden |
Opmerking
Bij andere ligging van de lijnstukken moet het bewijs iets worden aangepast.
[einde Opmerking]
| figuur 1c | 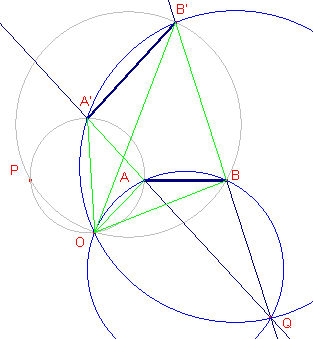 |
De gelijkvormigheid van de driehoeken OAB en OA'B' heeft ook de
gelijkvormigheid van de driehoeken OAA' en OBB' tot gevolg (en omgekeerd). Het lijnstuk BB' is dus beeld van AA' bij dezelfde draaivermenigvuldiging (met centrum O); zie figuur 1c. Zij nu Q het snijpunt van AA' en BB', dan gaan de omcirkels van de driehoeken QAB en QB'A' eveneens door het punt O. We hebben hiermee bewezen (voor de lijnen AB, A'B', AA', BB'):
|
Opmerking
Zie voor een ander bewijs van bovengenoemde stelling de pagina "De stelling van Miquel".
Op die pagina staat ook een CabriJavapplet
die de stelling illustreert.
[einde Opmerking]
2. De som van twee
draaivermenigvuldigingen ![]()
We gaan uit van twee draaivermenigvuldigingen. We bewijzen nu:
| Stelling 1 De som van twee draaivermenigvuldigingen D1(O1, h1, k1) en D2(O2, h2, k2) is - indien k1k2 = 1 en h1 + h2 = 360, een translatie; - anders, een draaivermenigvuldiging over de hoek h1 + h2 met factor k1k2. |
Bewijs: zie figuur 2.
| figuur 2 | 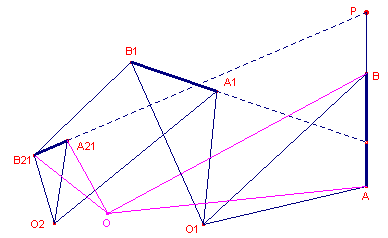 |
We bekijken het beeld van het lijnstuk AB (als deel van een figuur F)
onder de afbeelding D2oD1: D1(AB)=A1B2; D2(A1B1)=D2D1(AB)=A21B21. Uit de opvolgende vermenigvuldigingen vinden we eenvoudig: A21B21/AB = A21B21/A1B1 x A1B1/AB = k1k2 Uit de rotaties volgt direct (zie de pagina "Rotaties"), dat de lijnstukken A21B21 en AB dan een hoek h1 + h2 vormen. Het bijzondere geval (de translatie) volgt eveneens uit de eigenschappen van de som van twee rotaties. � |
3. Centrum van de som
![]()
Weer uitgaande van D1(O1, h1,
k1) en D2(O2,
h2, k2) hebben we (zie
figuur 3):
| figuur 3 | 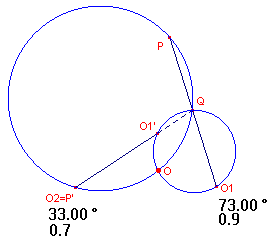 |
D2D1(O1) = O1' Zij P het punt waarvoor geldt D2D1(P) = O2. Dan geldt D2D1(O1P) = O1'O2 We kunnen het punt O, het centrum van de afbeelding D2D1 dus vinden met behulp van de lijnstukken O1P en O1'O2. Zij Q het snijpunt van de dragers van deze lijnen. Het punt O is dan het tweede snijpunt van de omcirkels van de driehoeken QPP' en QO1O1' (zie voor het bewijs de pagina "Bewegingen", paragraaf 2.3). |
Opmerking
Is A'B' het beeld van een lijnstuk AB bij een draaivermenigvuldiging, en is Q het snijpunt
van de dragers, dan is O het tweede snijpunt van de omcirkels van de driehoeken QAB en
QA'B'.
[einde Opmerking]
4. Som als puntspiegeling
![]()
We bekijken nu de som van de draaivermenigvuldigingen (90�, k) en (90�, 1/k).
| Stelling 2 De som van twee draaivermenigvuldigingen D1(O1, 90�, k) en D2(O2, 90�,1/k) is een puntspiegeling om het punt O dat de top is van de driehoek O1OO2 waarbij OO2 = OO1 en de basishoeken gelijk zijn aan arctan(1/k). |
Bewijs: zie figuur 4.
| figuur 4 | 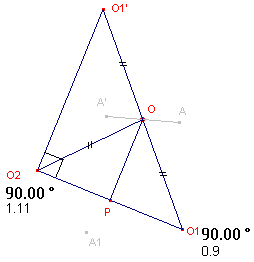 |
Duidelijk is nu dat we een rotatie hebben over 180� (immers k1k2 = 1).
Dus hebben we een puntspiegeling. Nu is D2D1(O1) = D2(O1) = O1'. Het punt O is dus het midden van het lijnstuk O1O1'. Dus is OO1 = OO2 (Thales-eigenschap in een rechthoekige driehoek). Stel O1O2 = a. Dan is O2O1' = (1/k) . a Zodat tan(OO2O1) = OP/O2P = O2O1'/O2O1 = 1/k. � |
5. Sylvester's rotator
![]()
Op de pagina "Rotaties" wordt een stangenmechanisme
behandeld, waarmee een draaivermenigvuldiging van een figuur wordt uitgevoerd, de
zogenoemde rotator (of pantograaf) van Sylvester.
[draaiverm.htm] laatste wijziging op: 19-08-02