Stelling van Thales (Prop. III-31)
Stelling | Omgekeerde
stelling | Prop III-31 (Elementen) | Toepassing ][ DK
& Meetkunde
Stelling - stelling van Thales
Van een rechthoekige driehoek is het midden van de schuine zijde het middelpunt van de
omgeschreven cirkel. |
Bewijs: zie figuur 1.
| figuur 1 |
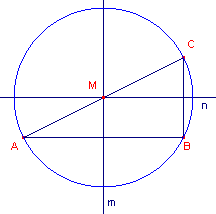 |
In deze figuur hebben we
- driehoek ABC waarvan hoek B recht is;
- m is de middelloodlijn van AB, n is de middelloodlijn van CB.
Omdat m evenwijdig is aan CB en door het midden gaat van AB, gaat m ook
door het midden M van AC (stelling van de middenparallel; zie Opmerking).
Hetzelfde geldt voor de lijn n.
Voor het punt M geldt dus MA = MB en ook MC = MB.
M ligt dus op gelijke afstanden van A, B, C.
M is dus middelpunt van de omgeschreven cirkel van driehoek ABC. �
Klik hier  voor een animatie van de stelling
voor een animatie van de stelling |
Opmerking
Deze stelling is genoemd naar Thales van Milete (624-547 vC). Vermoedelijk is de omgekeerde stelling de oudste ("netjes") bewezen
meetkunde-stelling.
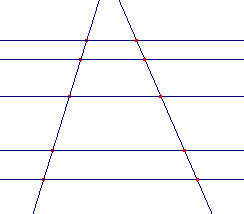
| figuur 2 |
 |
De stelling die in het bewijs is aangegeven met "stelling van de
middenparallel", wordt soms ook wel naar Thales genoemd, maar dan in een wat
algemenere vorm:
Stelling
Evenwijdige lijnen snijden van twee lijnen evenredige stukken af. (zie
figuur 2). |
|
[einde Opmerking]
Stelling - omgekeerde stelling van
Thales
Van een driehoek ABC waarvan AC de middellijn is van de omgeschreven cirkel, is hoek B
recht
of ook wel
Een hoek beschreven in een halve cirkel is recht. |
Bewijs: zie figuur 3.
| figuur 3 |
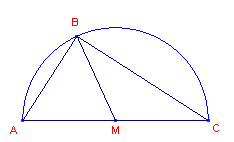 |
In deze figuur is M het midden van het lijnstuk AC.
M is het middelpunt van de cirkel met straal MA.
Het punt B is een punt van deze cirkel. We zullen nu bewijzen dat hoek B een rechte hoek
is.
Omdat MA = MB zijn de hoeken MAB en MBA gelijk.
Omdat MC = MB, zijn de hoeken MBC en MCB gelijk.
De som van deze hoeken is gelijk aan 180�. De hoeken MBA en MBC zijn dus samen 90�.
Met andere woorden, hoek B is een rechte hoek.� |
Klik hier  voor een animatie van de stelling.
voor een animatie van de stelling.
Opmerking
Deze laatste stelling komt voor als Propositie 31 in Boek III
van de Elementen van Euclides van Alexandri� (~325 - ~265 vC). Deze
propositie is echter uitgebreider dan de hierboven genoemde stelling.
Propositie III - 31
In een cirkel is de hoek in een halven cirkel een rechte, die in een grooter segment
kleiner dan een rechte, die in een kleiner segment grooter dan een rechte. En ook is de
hoek van het grootere segment grooter dan een rechte, de hoek van het kleinere segment
kleiner dan een rechte. |
Opmerking
Dijksterhuis merkt hierbij op (in De Elementen van Euclides, Noordhoff,
1930, deel II, pg. 41):
Het tweede deel der propositie is blijkbaar, [..], een
overblijfsel uit den tijd, dat de niet-rechtlijnige hoeken nog een rol speelden.
[einde Opmerking]
Hieronder volgt het bewijs (van het eerste deel van Prop. 31) zoals
dat voorkomt in Boek III van de Elementen.
| Bewijs: |
|
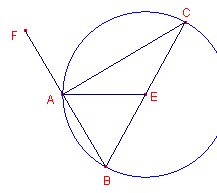 |
[...]
Men trekt AE en verlengt BA naar F.
Daar BE = EA, is ook ABE = BAE. Zo is ook, daar CE = EA, ACE = CAE. Dus is ook de gehele
BAC = ABC + ACB.
Bij driehoek ABC is buitenhoek FAC = ABC + ACB. Dus is BAC = FAC. Dus zijn beide hoeken
recht. Dus is hoek BAC in driehoek BAC een rechte hoek.
[...].� |
Toepassing
Gegeven:
Een cirkel met middelpunt O en een punt A buiten die cirkel.
Te construeren:
De raaklijnen uit het punt A aan cirkel O. |
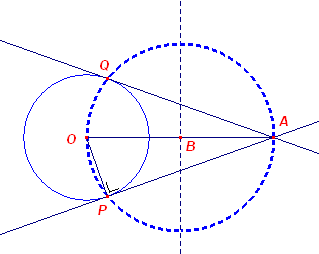
Constructie:
Bepaal het midden B van het het lijnstuk OA (met de middelloodlijn van het lijnstuk OA).
Teken dan de cirkel B(, BA). Deze cirkel snijdt de gegeven cirkel O in de punten P en Q.
De lijnen AP en AQ zijn dan de (gezochte) raaklijnen uit A aan cirkel O.
Bewijs:
Hoek OPA = 90�, volgens de Omgekeerde stelling van Thales. Dus is AP
raaklijn aan cirkel O.
Analoog voor AQ.� |
 |

[thales.htm] laatste wijziging op: 27-10-2004




