Bewegingen in het platte vlak
Zie ook de pagina "Rotaties"
Zie ook de pagina "Gelijkvormigheid
(van drie figuren)"
Opmerking
Op deze pagina wordt met h(XYZ) bedoeld de hoek gevord door de lijnstukken XY en ZY
(hoekpunt Y).
[einde Opmerking]
1. Bewegingen van congruente
figuren 
1.1. Inleiding 
Zijn F en F' twee direct congruente figuren (ze hebben dezelfde
ori?ntatie) in het platte vlak, dan kunnen deze figuren door middel van rotatie en/of
translatie samenvallen.
We beschouwen in hetgeen volgt de tussenliggende stappen die de figuur F doen samenvallen
met de figuur F'.
We kunnen dit bij een "oneindig" aantal stappen opvatten als een beweging.
1.2. Twee stellingen 
Zij F een figuur (bijvoorbeeld een driehoek) die wordt geroteerd om een punt O; dat wil
zeggen, dat de figuur beweegt rond een punt O, dat tot de figuur behoort, maar zelf
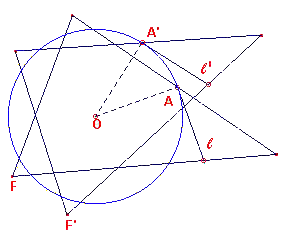
invariant is (zie figuur 1).
| figuur 1 |
 |
figuur 2 |
 |
In dit geval beschrijft elk punt van F een cirkel met middelpunt O (omdat de
afstand OA constant blijft); elke lijn l van F is ?f steeds rakend aan een vaste
cirkel met centrum O ?f gaat steeds door O (omdat de afstand van O tot l constant
blijft).
Het punt O is centrum van een rotatie voor elk tweetal posities van F.
Klik hier  voor een animatie
van figuur 1.
voor een animatie
van figuur 1.
Beschouwen we vervolgens een translatie van een figuur in een bepaalde richting, nl.
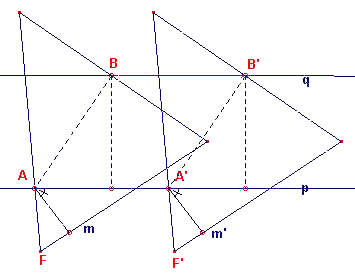
die van een gegeven lijn p (zie figuur 2). Bij deze beweging is de lijn p
(niet-puntsgewijs) invariant; hij beweegt langs zichzelf). Elk punt B van de figuur
beschrijft een lijn evenwijdig aan p (omdat de afstand van B tot P constant is).
Elke lijn m die niet evenwijdig is aan p beweegt zo, dat deze evenwijdig is
met de lijn in de uitgangspositie (omdat de hoek tussen m en p constant is).
Elke lijn q evenwijdig aan p is (niet-puntsgewijs) invariant (omdat de
afstand van q tot p constant is).
Bij elk tweetal posities van de figuur F hoort dus een translatie in de richting van p.
Als een figuur F zo beweegt, dat twee evenwijdige lijnen p en q steeds
door twee punten A en B (A op p, en B op q) gaan, dan is p
(niet-puntsgewijs) invariant (omdat de hoek tussen AB en p constant is.
Ook hier hebben we dus te maken met een translatie (zie hierboven, en zie
figuur 2).
Het wordt wat gecompliceerder als we twee niet-evenwijdige lijnen p en q
beschouwen die steeds door twee gegeven punten A (op p) en B (op q) gaan.
Voor dit geval bewijzen we de volgende
Stelling 1
Als een figuur F zo wordt bewogen in een vlak, dat twee gegeven niet-evenwijdige lijnen
p en q van F steeds door twee vaste punten A en B gaan, dan geldt
voor elke andere lijn van F ?f dat deze steeds gaat door een ander vast punt van F, ?f
dat deze steeds raakt aan een cirkel in het vlak. |
Bewijs: (zie figuur 3)
We gaan uit van de figuren F en F1, die we voor de duidelijkheid niet in figuur 3 hebben
getekend. Zijn O en O1 de snijpunten van de lijnen p en q en van p1
en q1. De punten O en O1 liggen op een cirkelboog van de cirkel, S, die de
meetkundige plaats is van de punten waaronder de koorde AB onder de hoek tussen p
en q wordt gezien.
| figuur 3 |
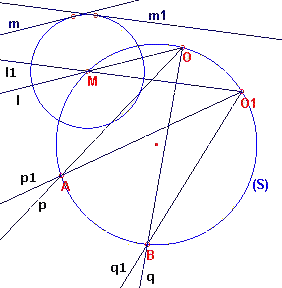 |
Zijn nu l en l1 twee posities van een lijn l die
door O gaat. Stel nu M en M1 zijn de snijpunten van l met de cirkel S. Omdat
h(MOA) = h(M1O1A) (omdat de hoek tussen l en p
constant is), blijkt dat bg(AM) = bg(AM1). En dit wil zeggen, dat M=M1.
We hebben dus laten zien, dat alle posities van de lijn l door M gaan.
Zij nu m een lijn die niet door O gaat. Trekken we nu een lijn l door O
evenwijdig aan m, dan weten we dat alle posities van deze lijn l door het
punt M gaan. Omdat de afstand tussen de lijnen m en l niet verandert, moeten
alle posities van de lijn m raken aan een cirkel met middelpunt M en met een straal
die gelijk is aan de afstand van l en m.
Hiermee is de stelling bewezen. ?
Kilk hier  voor een animatie
van figuur 3. voor een animatie
van figuur 3. |
Gevolg
We bekijken nu een gevolg van bovenstaande stelling.
| figuur 4 |
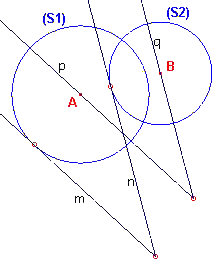 |
Stel dat de figuur F zo in het vlak beweegt dat twee niet evenwijdige
lijnen m en n van de figuur steeds raken aan twee gegeven cirkels S1 en S2
(zie figuur 4, waarin we weer voor de duidelijkheid de figuur F zelf hebben weggelaten).
De lijnen p en q die evenwijdig zijn met m en n gaan door de
middelpunten A en B van deze cirkels.
De afstand tussen m en p is gelijk aan de straal van S1; de afstand tussen n
en q is gelijk aan de straal van cirkel S2. Omdat die afstanden tijdens de beweging
niet veranderen, gaat de lijn p steeds door het vaste punt A. Evenzo vinden we dat
de lijn q steeds door het vaste punt B gaat.
We kunnen nu stelling 1 toepassen; we zien dat bij een dergelijke beweging elke lijn van F
?f steeds raakt aan een vaste cirkel, ?f steeds gaat door een gegeven vast punt.[einde
Gevolg] |
Als de figuur F zo in het vlak beweegt, dat twee punten A en B van de figuur
evenwijdige lijnen p en q beschrijven, dan zijn alle posities van het
lijnstuk AB aan elkaar evenwijdig (omdat de hoek tussen AB en p niet verandert).
Elke twee posities van F kan kunnen dus uit elkaar ontstaan door een translatie in de
richting van de lijn p. We hebben dus te maken met een translatie van de figuur die
we reeds eerder bekeken hebben (zie figuur 2).
De situatie wordt ingewikkelder als de eindpunten van een lijnstuk AB van de figuur
bewegen op twee niet evenwijdige (dus elkaar snijdende) lijnen. In dit geval
bewijzen we de volgende stelling.
Stelling 2
Als een figuur F zo in een vlak beweegt dat twee punten A en B in dat vlak lijnen p en
q beschrijven die elkaar snijden in het punt O, dan bestaat er een cirkel S, gekoppeld aan
figuur F, waarvan elk punt een lijn beschrijft die door O gaat. |
| figuur 5 |
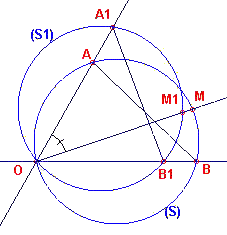 |
Bewijs: (zie figuur 5) Zijn F en F1 twee posities van
de figuur F (in de figuur zijn beide wederom niet getekend). AB enA1B1
zijn de bij behorende standen van het in de stelling bedoelde lijnstuk. We bekijken nu de
cirkel S door O, A en B. Deze cirkel hoort bij de positie van F. De bij de positie van F1
behorende cirkel is S1. Duidelijk is, dat ook S1 door het punt O gaat (omdat
bg(AB) van S gelijk is aan bg(A1B1) van S1; deze hoek is
in beide gevallen gelijk aan 2h(AOB). Zij nu M een punt van cirkel S en M1
het bijbehorende punt van cirkel S1. Uit de congruentie van F en F1
volgt nu onmiddellijk dat bg(AM) = bg(A1M1). |
Dit betekent dat de ingeschreven hoeken op die bogen ook gelijk zijn:
h(AOM) = h(A1OM1). En hieruit volgt nu, dat de lijnen OM
en OM1 samenvallen. Gevolg: elk punt M op de omtrek van S beweegt over een lijn
door O. En dit moest bewezen worden. ?
Merk op dat het middelpunt N van S beweegt langs een cirkel met middelpunt O. Dit volgt
uit het feit, dat alle cirkels S, waarvan de straal dus constant is, door het punt O gaan.
Klik hier  voor een animatie
van figuur 5.
voor een animatie
van figuur 5.
2. Bewegingen van gelijkvormige
figuren 
2.1. Inleiding 
Figuren F en F1 heten direct gelijkvormig,
als figuur F1 uit figuur F ontstaat door een vermenigvuldiging ten opzichte van
een punt O (het centrum van de vermenigvuldiging) met een getal k 0 (de
vermenigvuldigingsfactor).
Figuren F1 en F' heten rotatiecongruent
als F' uit F1 ontstaat door een rotatie om een punt (het centrum
van de rotatie) over een bepaalde hoek (de rotatiehoek).
We kunnen nu de som (de volgorde is onbelangrijk) van beide operaties uitvoeren. Een
dergelijke meetkundige afbeelding heet draaivermenigvuldiging (zie figuur 6).
| figuur 6 |
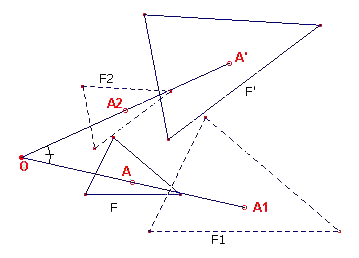 |
De figuren F en F' noemen we draaigelijkvormig.
Uit het bovenstaande volgt direct dat ook de omgekeerde bewerking een
draaivermenigvuldiging is: de figuur F kan uit F' ontstaan door opvolgend een rotatie over
de hoek - en een vermenigvuldiging met het getal 1/k (beide ten opzichte van het
punt O). Ook nu kunnen we de alle tussenliggende stappen beschouwen die figuur F doen
overgaan in figuur F' |
Ook nu zullen we spreken van een beweging. Bij deze beweging verandert de vorm van de
figuur niet, echter wel de afstanden tussen punten van de figuur (er is dus nog steeds
sprake van gelijkvormigheid). Spreken we in hetgeen volgt over "bewegen", dan
bedoelen we in beweging op deze manier.
Zie de paragraaf Constructies voor eenvoudige constructies bij een
draaivermenigvuldiging.
Zie de pagina "Draaivermenigvuldiging"
voor verdere eigenschappen van deze afbeelding.
2.2. Invariantie 
Het zal blijken, dat bij bewegingen van gelijkvormige figuren invariante punten en lijnen
een belanfrijke rol spelen.
Stelling 3
Beweegt een figuur F zo, dat een punt O van F invariant is, en is F' het beeld van F,
waarbij F en F' gelijkvormig zijn, dan zijn F en F' of (1) congruent of (2) direct
gelijkvormig congruent of (3) draaigelijkvormig. |
Bewijs:
(1) Is A een punt van F dat bij de beweging een cirkel met middelpunt O beschrijft, dan is
verandert de afstand tussen O en A dus niet. In dit geval beschrijven dus alle punten van
F een cirkel. We hebben dus te maken met een rotatie. Dus F is congruent met F' (zie figuur 1).
| figuur 7 |
 |
figuur 8 |
 |
(2) (zie figuur 7) Beschrijft het punt A een lijn door O, dan
beschrijft elk ander punt B eveneens een lijn door O (omdat de hoek BOA niet verandert,
vanwege de gelijkvormigheid van de figuren F en F'). Bij een dergelijke beweging kan F'
dus steeds teruggebracht worden naar zijn oorspronkelijke positie door een
vermenigvuldiging met centrum O. F en F' zijn dus direct gelijkvormig.
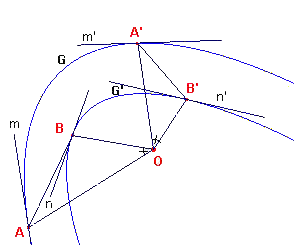
(3) (zie figuur 8) We gaan er nu van uit, dat bij een dergelijke
beweging een punt A van de figuur F een willekeurige kromme G (bijvoorbeeld een cirkel of
cirkelboog) beschrijft. We tonen nu aan, dat elk ander punt B (met uitzondering van het
punt O) een met G gelijkvormige kromme G' beschrijft. Zij F de figuur in de
oorspronkelijke positie en F' een andere positie van F. A, B, A', B' zijn overeenkomstige
posities van punten van F en F'. Omdat er sprake is van gelijkvormigheid, geldt
OAB ~ OA'B'. Dus h(B'OA') = h(BOA) = en OB'/OA' =
OB/OA = k. Er is nu sprake van draaivermenigvuldiging met factor k
over hoek en centrum O, waarbij B' wordt afgebeeld op A'. Omdat F' een willekeurige
positie is van de figuur, betekent dit, dat deze draaivermenigvuldiging de kromme G',
beschreven door het punt B, afbeeldt op de kromme G, beschreven door het punt A. Maar als
twee krommen op elkaar kunnen worden afgebeeld met een draaivermenigvuldiging, dan zijn ze
gelijkvormig. ?
Stelling 4
Als een lijn m van een figuur F, die niet door O gaat, raakt aan een kromme
G, dan raakt elke andere lijn n van F aan een kromme G' die gelijkvormig is
met G. |
Bewijs: (zie figuur 8)
Zoals uit stelling 3 blijkt, is de kromme G' het beeld van de kromme G
bij een draaivermenigvuldiging met centrum O, waarbij m op n wordt
afgebeeld. ?
2.3. Constructies 
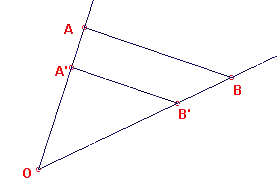
| figuur 9 |
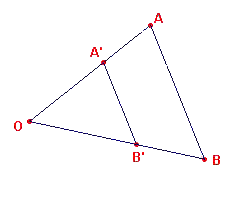 |
We laten nu zien hoe we het centrum van draaivermenigvuldiging O kunnen
construeren bij gegeven lijnstukken AB en A'B'. (1) Als de lijnstukken evenwijdig
zijn is er sprake van directe gelijkvormigheid. In dit geval is O het snijpunt van de
lijnen AA' en BB' (zie figuur 9). |
| figuur 10a |
 |
figuur 10b |
 |
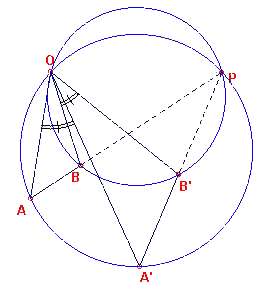
(2) Is de hoek tussen de lijnstukken geen veelvoud van 180o, dan kiezen
we het punt P als snijpunt van de lijnen AB en A'B' (zie figuur 10).
De omgeschreven cirkels van AA'P en BB'P gaan door het gezochte rotatiecentrum (niet
zijnde het punt P). Dit laatste vraagt echter wel degelijk een
Bewijs.
h(AOA') = h(APA'), omtrekshoeken op dezelfde cirkel; de rotatiehoek AOA' is dus
gelijk aan de hoek tussen de lijnstukken AB en A'B'.
h(BOB') = h(PBB'), omtrekshoeken op dezelfde cirkel; de rotatiehoek BOB' is dus
eveneens gelijk aan de hoek tussen AB en A'B'. Hieruit volgt dus eenvoudig, dat
h(AOB) = h(A'OB'). O is dus het gezochte rotatiecentrum.
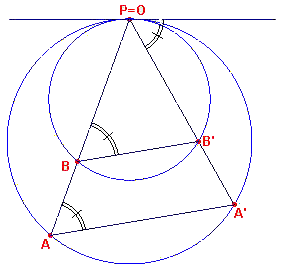
Als de beide cirkels elkaar raken in P (zie figuur 10b), dwz. als
h(PAA') = h(PBB') -deze hoeken zijn beide gelijk aan de hoek tussen de lijn
PB'A' en de gemeenschappelijke raaklijn in P, dan valt O met P samen. Immers, wegens de
gelijkvormigheid geldt PA'/PA = PB'/PB. ?
Gevolg
Het centrum van de draaivermenigvuldiging die AB overvoert in A'B' valt samen met het
centrum van draaivermenigvuldiging, die AA' overvoert in BB'. We hebben immers:
h(AOA') = h(BOB') = a; OA'/OA =
OB'/OB = k, waaruit volgt
h(AOB) = h(A'OB'), zie figuur 10c, waarin b = a + h(A'OB) en OA/OB = OA'/OB' = l.
| figuur 10c |
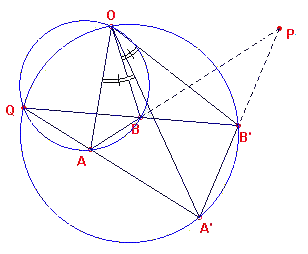 |
Hieruit volgt, dat het centrum O eveneens gevonden kan worden als het
(tweede) snijpunt van de cirkels beschreven rond de driehoeken ABQ en A'B'Q, waarbij Q het
snijpunt is van de lijnen AA' en BB' (of als het snijpunt van AB en A'B', in het geval
dat AA'//BB'). [einde Gevolg] |
2.4. Conclusies 
We geven nu twee belangrijke stellingen die betrekking hebben op bewegingen die het gevolg
zijn van draaivermenigvuldigingen.
Stelling 5
Als een figuur F onderhevig is aan een gelijkvormige beweging en wel zo, dat drie
punten A, B, C van F drie lijnen beschrijven (die geen gemeenschappelijk punt hebben), dan
beschrijft elke lijn van F een rechte lijn.Stelling 6
Als een figuur F onderhevig is aan een gelijkvormige beweging, waarbij drie
lijnen l, m en n van F, die geen gemeenschappelijk punt hebben, steeds door drie
vaste punten gaan, dan gaat elke lijn van F steeds door een vast punt, en beschrijft elk
punt van F een cirkel. |
Bewijs van stelling 5: (zie
figuur 11)
We zullen aantonen, dat elke twee posities van F hetzelfde centrum van rotatie O hebben
(dit betekent, dat een punt van F invariant is onder de beweging). Hieruit zal dan volgen,
dat alle punten van F kromme lijnen beschrijven die gelijkvormig zijn aan de kromme die
beschreven wordt door het punt A; dus rechte lijnen.
| figuur 11 |
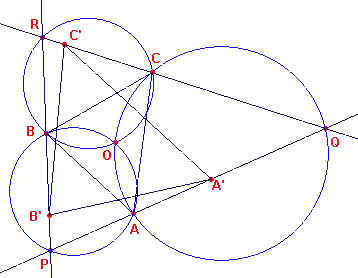 |
De lijnen waarlangs A, B, C zich bewegen snijden elkaar in P, Q, R. Zijn
F en F' twee posities van de beschouwde figuur, waartoe opvolgend de punten A,B,C en
A',B',C' behoren. Het centrum van rotatie O van F en F' is hetzelfde als het
rotatiecentrum van de lijnstukken AB, A'B' en AC, A'C'. Zoals we hierboven (in de
paragraaf Constructies) hebben gezien, ligt het centrum van de rotatie van de lijnstukken
AB en A'B' op de omgeschreven cirkels van ABQ en A'B'Q, waarbij Q het snijpunt is van AA'
en BB'. |
In dit geval houdt dit in, dat O moet liggen op de omgeschreven cirkel van ABP (en die
van A'B'P). Op dezelfde manier kunnen we aantonen dat O moet liggen op de omgeschreven
cirkel van ACQ (bij beschouwing van de lijnstukken AC en A'C').
Het rotatiecentrum van de figuren F en F' is dus bepaald als snijpunt van de omgeschreven
cirkels van ABP en ACQ. en hangt dus niet af van de positie van de figuur F'. Maar dit
betekent, dat elk tweetal posities van F hetzelfde rotatiecentrum hebben. ?
Opmerking
| figuur 12 |
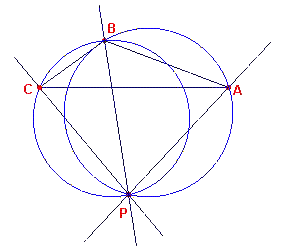 |
Als de lijnen die beschreven worden door de punten A,B,C door een
gemeenschappelijk punt P gaan (zie figuur 12), dan blijft de bewering
van de stelling in het algemeen geldig. Het bewijs verschilt dan niet van het hierboven
staande. Het gemeenschappelijk gelijkvormigheidspunt voor alle posities van F moet dan in
ieder geval samenvallen met de omgeschreven cirkels van ABP en BCP; en dat is het punt P. De
enige uitzondering hierop vinden we als de cirkels ABP en BCP samenvallen. Dit is het
geval, als A,B,C samen met P op dezelfde cirkel liggen., of, wat hetzelfde is, als
h(APB) + h(ACB) = 180o |
en daarbij de punten P en C aan verschillende kant van AB ligt, en ook als
h(APB) = h(ACB)
en daarbij P en C aan dezelfde kant liggen van AB.
In deze gevallen behoeft de stelling niet juist te zijn.
[einde Opmerking]
Bewijs van stelling 6:
We tonen aan, dat elk tweetal posities van de figuur F hetzelfde rotatiecentrum O hebben,
en dat een willekeurig punt A van F een cirkel beschrijft. Daaruit volgt dan volgens
stelling 3, dat elke lijn van F steeds door een bepaald vast punt gaat (omdat l
door een vast punt gaat) en dat elk punt van F een cirkel beschrijft (omdat A een cirkel
beschrijft).
We noemen de snijpunten van l, m, n opvolgend A, B en C
en geven de punten waardoor deze lijnen gaan, aan met P, Q en R (zie
figuur 13).
| figuur 13 |
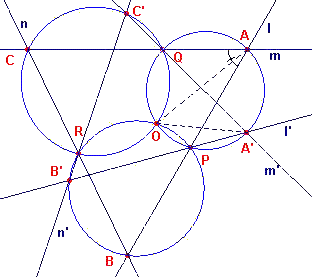 |
Het is direct duidelijk, dat A een cirkel beschrijft, omdat de grootte
van de hoek QAP bewaard moet blijven tijdens de beweging. (De hoeken tussen de lijnen l,
m, n blijven eveneens onveranderd wegens de gelijkvormigheid). Zijn
nu F en F' twee verschillende posities van de figuur, waarbij l, m, n
en 1', m', n' de overeenkomstige lijnen van die figuren zijn.
Zij A,B,C en A',B',C' de betreffende punten van F en F'. Als O het centrum is van de
rotatie, dan is hoek AOA' de hoek van de draaivermenigvuldiging en deze is dus gelijk aan
de hoek tussen l en l' (en tussen m en m'). |
Dus h(AOA') = h(APA') = h(AQA'), hetgeen wil zeggen, dat O ligt op
de cirkel door B, B', P en R. Hieruit volgt, dat het rotatiecentrum O het snijpunt is van
de omgeschreven cirkels van APQ en BRR. Dit centrum is dus niet afhankelijk van de
specifieke positie van F'. Daaruit volgt dus, dat elke twee posities van F hetzelfde
rotatiecentrum hebben. ?
De figuren op deze pagina zijn gemaakt met Cabri Geometry II.

[bewegingen.htm] laatste wijziging op: 12-08-2002














