Overzicht ][ Euler-cirkels | Meetkunde
1. Inleiding
![]()
We herhalen hier de definitie van koordenvierhoek, zoals deze staat op de pagina "Middelloodlijn, ...":
| Definitie Een convexe vierhoek heet koordenvierhoek als de hoekpunten op ��n cirkel liggen (concyclisch zijn). |
| figuur 1 | 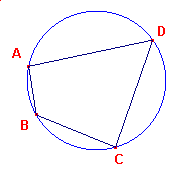 |
De belangrijkste eigenschap van een koordenvierhoek, naast het feit dat
de hoekpunten ervan concyclisch zijn, is vastgelegd in de op genoemde pagina vermelde
stelling (daar stelling 5):
|
Gevolgen
| figuur 2 | 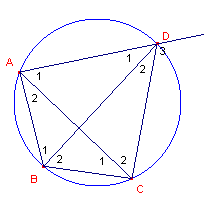 |
[1] In nevenstaande koordenvierhoek ABCD geldt dan: �A1 = �B2 �A2 = �D2 �B1 = �C2 �C1 = �D1 �D3 = �B12 |
[2]
Vier punten liggen dan en slechts dan op een cirkel als een van de volgende gevallen zich
voordoet:
1. C en D liggen aan dezelfde kant van AB en �ACB = �ADB
2. A en C liggen aan verschillende kanten van BD en �BAD + �BCD = 180�.
[einde Gevolgen]
Opmerking
De eigenschappen van de koordenvierhoek kunnen worden gebruikt bij een
"elementair" bewijs van de Stelling van Pascal voor
cirkels. Dit bewijs is gebaseerd op de Stelling van Miquel.
Klik hier voor een geZIPt
Word-document waarin bedoeld bewijs is opgenomen [ca. 38kB].
[einde Opmerking]
2.
Eigenschappen in een koordenvierhoek ![]()
2.1. Stelling van Ptolemaeus
| Stelling 1b ALS ABCD is een koordenvierhoek DAN de som van de producten van lengtes van de paren overliggende zijden is gelijk aan het product van de lengtes van de diagonalen. |
Klik hier voor het gebruikelijke bewijs.
Klik hier voor een bewijs met behulp van
inversie.
Klik hier voor de stelling van Casey waarvan de
stelling van Ptolemaeus een bijzonder geval is.
2.2.
Diagonaaldriehoeken ![]()
Een driehoek met drie van de vier hoekpunten van de koordenvierhoek als hoekpunt heet diagonaaldriehoek.
� 2.2.1. Hoogtepunten
| Stelling 2 Zijn Ha, Hb, Hc, Hd hoogtepunten van de diagonaaldriehoeken van koordenvierhoek ABCD, dan is HaHbHcHd congruent met ABCD. |
Bewijs: zie allereerst figuur 3.
| figuur 3 | 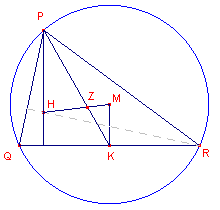 |
In de hiernaast staande figuur is HM de lijn van Euler. Het zwaartepunt Z
van driehoek PQR ligt hierop, en wel zo, dat MZ : ZH = 1 : 2
(zie de pagina "De cirkel van Feuerbach en de lijn van
Euler"). Nu zijn de driehoeken KMZ en PHZ gelijkvormig. Hieruit volgt, dat PH = 2 MK. Dus: Het bovenste hoogtelijnstuk is gelijk aan 2 maal de afstand van het omcentrum van de driehoek naar de zijde waarop die hoogtelijn staat. |
Opmerking
We kunnen de eigenschap in figuur 3 ook direct bewijzen, uitgaande van
de punten M en K.
Teken de zwaartelijn PK en daarop het zwaartepunt Z. Bepaal het punt H zo, dat
MZ : ZH = 1 : 2. De driehoekem KMZ en PHZ zijn nu
gelijkvormig. Waaruit volgt, dat PH evenwijdig is met MK.
Dus PH is een hoogtelijn. De punten M en Z zijn vast. Dus is ook het punt H vast. H is dus
het hoogtepunt van driehoek PQR.
[einde Opmerking]
| figuur 4a | 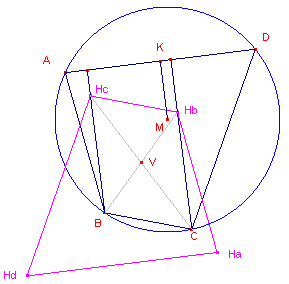 |
Bekijken we nu in figuur 4a de hoogtelijnen BHc
(in driehoek ABD) en CHb (in driehoek ACD). Voor de bovenste hoogtelijnstukken daarvan geldt dus dat BHc = 2 KM en CHb = 2 KM Dus BHc = CHb en ook BHc // CHb. BCHcHb is dus een parallelogram. Zij V het snijpunt van de diagonalen daarvan, dan onstaat HaHbHcHd dus uit ABCD door vermenigvuldiging tov. V met factor -1. � |
| figuur 4b | 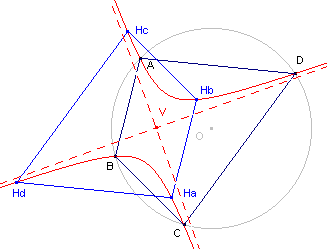 |
Gevolg De verbindingslijnen AHa, BHb, CHc en DHd zijn concurrent in het punt V. Deze eigenschap gebruiken we in de volgende paragraaf (Voetpuntsrechten). [einde Gevolg] Opmerking |
� 2.2.2.
Voetpuntsrechten (lijnen van Wallace-Simson) en negenpuntscirkels ![]()
Zoals bekend (indien niet, zie de betreffende paragraaf op de pagina "Cirkel van Feuerbach") liggen de voetpunten van een punt
P van de omgeschreven cirkel van een driehoek op een rechte lijn, de voetpuntsrechte
of ook wel rechte van Wallace of de lijn van Simson).
We hebben nu:
| Stelling 3 De voetpuntsrechten van de hoekpunten van een koordenvierhoek ten opzichte van de ("overblijvende") diagonaaldriehoek zijn concurrent. |
Bewijs: zie figuur 5.
| figuur 5 | 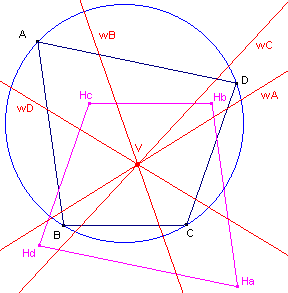 |
De cirkel van Feuerbach (negenpuntscirkel)
van een driehoek ontstaat uit de omgeschreven cirkel door vermenigvuldiging daarvan ten
opzichte van het hoogtepunt met de factor �. Bekijken we nu driehoek ABC en het punt D. Uit de genoemde vermenigvuldiging blijkt dus, dat met midden van het lijnstuk DHd (Hd is het hoogtepunt van driehoek ABC) op de voetpuntsrechte van D tov. driehoek ABC ligt. Maar dit midden is het punt V (zie het Gevolg van stelling 2). V ligt dus op elke voetpuntsrechte wI van de hoekpunten van de koordenvierhoek Deze voetpuntsrechten zijn dus concurrent in het punt V. � |
Gevolg van stelling 3:
| Stelling 4 [1] De negenpuntscirkels van de diagonaaldriehoeken van een koordenvierhoek snijden elkaar in het punt V (het Euler-punt van de koordenvierhoek). [2] De negenpuntscentra van de diagonaaldriehoeken vormen een koordenvierhoek die gelijkvormig is met de oorspronkelijke koordenvierhoek. |
Bewijs: van [4.1] zie figuur 6a.
| figuur 6 a |
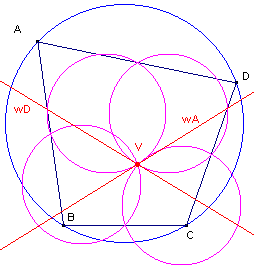 |
Uit de vermenigvuldiging met � van de omgeschreven cirkel van driehoek
ABC ten opzichte van het een hoogtepunt Hd (zie Stelling 3),
volgt dat het beeld van D, en dat is het punt V, op de negenpuntscirkel van driehoek ABC
ligt. Dit geldt voor elke vermenigvuldiging tov. H i, zodat de negenpuntscirkels van de diagonaaldriehoeken van de koordenvierhoek het punt V gemeenschappelijk hebben. Opmerking |
| figuur 6 b |
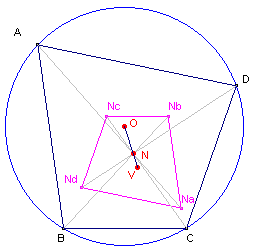 |
Bewijs: van [4.2] Het centrum van vermenigvuldiging is in dit geval het punt N, dat gelegen is op het lijnstuk OV (waarbij O het middelpunt is van de omcirkel). N ligt zo op OV, dat NV : NO = 1 :2. De factor is dus in dit geval -�. � Opmerkingen |
[2]
Het Euler-punt bestaat ook voor een willekeurige
vierhoek.
Zie hiervoor de pagina "Euler-cirkels"
[einde Opmerking]
| figuur 7 | 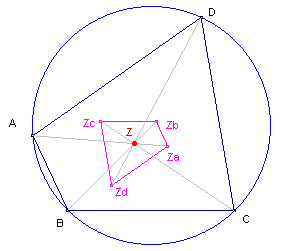 |
Zie verder het Cabri-werkblad "Zwaartepunten" |
� 2.2.4. Incentra en uitcentra ![]()
2.2.4.1. Incentra ![]()
Zagen we in de voorgaande paragrafen steeds een koordenvierhoek die gelijkvormig (of
congrent) was met de oorspronkelijke koordenvierhoek, bij de incentra
(middelpunten van ingeschreven cirkels) van de diagonaaldriehoeken krijgen we een
regelmatiger figuur.
| figuur 8 | 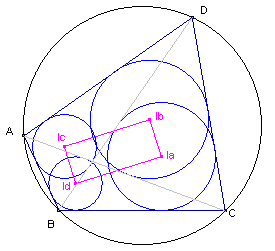 |
Voorafgaand aan het bewijs geven we allereerst twee hulpstellingen (zie daarvoor Hulpstelling 6.1 en Hulpstelling 6.2). |
|
| figuur 9 | 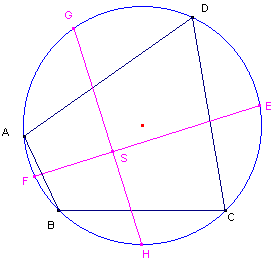 |
Bewijs: zie figuur 9. |
|
| figuur 10 | 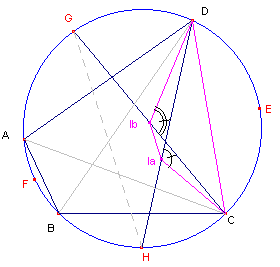 |
Bewijs: |
Dus �CIaD = �CIbD.
CIaIbD is dus een koordenvierhoek. �
We geven nu het bewijs van Stelling 6.
Bewijs van Stelling 6:
Zie daarvoor ook figuur 10.
In koordenvierhoek CIaIbD (zie Hulpstelling 6.2)
hebben we
�DIaIb = �DCIb
= �bgDG = �DHG,
waaruit dus volgt dat IaIb // GH.
Op dezelfde manier bewijzen we, dat IbIc // EF (zie figuur
8 en figuur 9).
Dus IaIbIcId is een rechthoek (immers EF en GH
staan loodrecht op elkaar; zie Hulpstelling 6.1).
Hiermee is Stelling 6 bewezen. �
2.2.4.2. Uitcentra ![]()
De uitcentra van een driehoek zijn de middelpunten van de drie aangeschreven
cirkels aan de zijden van die driehoek.
Bekijken we deze nu voor de 4 diagonaaldriehoeken van een koordenvierhoek, dan hebben we
dus 12 van deze centra.
Hierbij krijgen we een wel heel bijzondere ligging (zie figuur 11).
| figuur 11 | 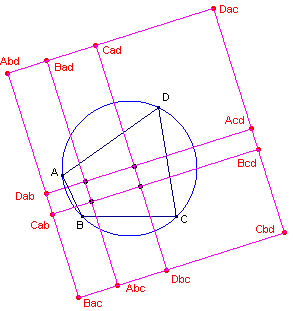 |
Op de pagina "Isogonalen" staat de volgende definitie:
| Definitie Twee lijnen l en m heten antiparallel ten opzichte van de lijnen p en q, indien er twee lijnen l' (// l) en m' (// m) zijn die met p en q isogonaal verwant zijn. |
Wat "isogonaal verwant zijn" betekent, staat ook op de pagina "Isogonalen", maar we geven de definitie hier in een iets andere vorm:
| Definitie Twee lijnen l en m heten isogonaal verwant tov. twee lijnen p en q, als ze elkaars spiegelbeeld zijn in de bissectrice van de hoek tussen p en q. |
Op grond van deze definities kunnen we nu eenvoudig bewijzen:
| Stelling 7 Twee overstaande zijden van een koordenvierhoek zijn antiparallel met de beide andere zijden. |
| figuur 12 | 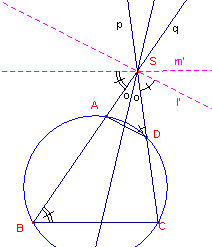 |
We bewijzen dat AD (= l) en BC (= m) antiparallel zijn
met CD (= p) en AB (= q). De lijnen l' en m' zijn door S (het snijpunt van p en q) evenwijdig aan l en m getrokken. Nu moet l' het beeld zijn van m' in de bissectrice van hoek S. Op grond van het feit, dat � B + � D = 180�, weten we, dat � B = buitenhoek bij D. We kunnen nu gemakkelijk afleiden (uit de evenwijdigheid van de paren lijnen), dat de bissectrice van hoek S ook de hoek tussen l' en m' middendoor deelt. Waaruit volgt, dat l' het beeld is van m' bij een spiegeling in de bissectrice van hoek S. � |
Opmerking
Deze eigenschap wordt gebruikt bij de definitie van de Tucker-cirkels van een driehoek.
Zie de pagina "Tucker-cirkels".
[einde Opmerking]
4. Nevencentrum, Euler-punt, Mathot-punt
| Definitie Het nevencentrum (of Mathot-punt) van een koordenvierhoek is het spiegelbeeld van omcentrum in het snijpunt van de verbindingslijnen van de middens van de paren overstaande zijden. |
Opmerking
Het snijpunt van de verbindingslijnen van de middens van de paren overstaande zijden van
een vierhoek is het zwaartepunt (van de hoekpunten) van die vierhoek.
Zie het Cabri-werkblad "Het
zwaartepunt van een veelhoek"
[einde Opmerking]
En dan hebben we
| Stelling 8 Het nevencentrum van een koordenvierhoek valt samen met het Euler-punt van die vierhoek |
Klik hier voor het bewijs van Stelling 8, en verdere gevolgen daarvan