Euler-cirkel

Euler-cirkels

Overzicht ][ Koordenvierhoeken | Feuerbach | Meetkunde

Zie ook de pagina "Complexe getallen en meetkundige bewijzen"

0. Overzicht

Definitie en inleiding
Euler-cirkels in een vierhoek
2.1. Willekeurige vierhoek / Euler-punt
2.2. Koordenvierhoek
Euler-cirkels in een koordenvijfhoek
Samenhang met een orthogonale hyperbool
Stelling van Poncelet-Brianchon

1. Definitie en inleiding
In onderstaande paragrafen behandelen we enkele eigenschappen van n-hoeken (n = 3, 4, 5) in samenhang met de cirkels van Euler en het concyclisch zijn van bijzondere punten, alsmede het verband tussen het punt van Euler van een vierhoek en een orthogonale hyperbool door de vierhoekpunten (naar Leonard Euler, 1707-1783, Zwitserland).

Definitie
De Euler-cirkel van een koorde van een cirkel met straal R is de cirkel met straal R/2 die als middelpunt het midden van de koorde heeft (zie figuur 1).

	figuur 1		figuur 2
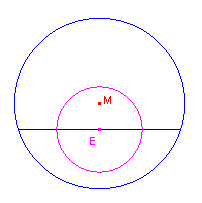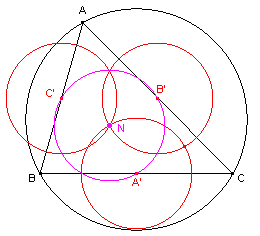				In figuur 2 zijn de Euler-cirkels van de zijden van driehoek ABC getekend; de zijden zijn dus opgevat als koorden van de omcirkel van ABC. De bijzondere eigenschappen van deze figuur zijn geformuleerd in stelling 1.

Stelling 1
De middelpunten van de Euler-cirkels van de zijden van een driehoek zijn concyclisch.
De Euler-cirkels van de zijden van een driehoek gaan door ��n punt.

Opmerkingen
[1]
De cirkel met middelpunt N die gaat door de middens van de zijden noemen we de Euler-cirkel van de driehoek.
In een ander verband wordt deze cirkel ook wel de Negenpuntscirkel of de cirkel van Feuerbach genoemd.
Het punt N heet ook wel Euler-punt van de driehoek.
[2]
De straal van de Euler-cirkel van een driehoek is dus R/2.
[einde Opmerkingen]

Bewijs van Stelling 1:

figuur 3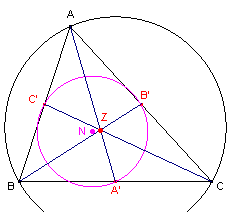

Zie figuur 3.
De Euler-cirkel van driehoek ABC onstaat uit de omgeschreven cirkel door vermenigvuldiging met de factor -� ten opzichte van het zwaartepunt Z van de driehoek. De straal van de Euler-cirkel is dus R/2.
Zij N het middelpunt van deze cirkel, dan is dus:
NA' = NB' = NC' = R/2.
De Euler-cirkels van de zijden van de driehoek gaan dus door N. �

Opmerking
Voor een uitvoeriger behandeling van deze eigenschappen wordt verwezen naar de pagina "De cirkel van Feuerbach".
[einde Opmerking]

2. Euler-cirkels in een vierhoek
2.1. Willekeurige vierhoek / Euler-punt
We gaan eerst uit van een willekeurige convexe vierhoek (dus niet noodzakelijk een koordenvierhoek).
Van de vier diagonaaldriehoeken (driehoeken met drie hoekpunten van de vierhoek als hoekpunt) van deze vierhoek tekenen we de Euler-cirkel (zie figuur 4).
Er blijkt:

figuur 4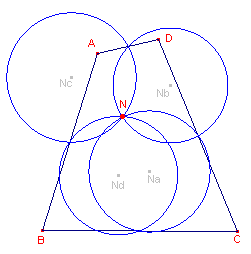

Stelling 2
De Euler-cirkels van de diagonaaldriehoeken van een vierhoek gaan door ��n punt.
Dit punt heet het Euler-punt van de vierhoek.

Bewijs: zie figuur 5.
Hierin zijn getekend de Euler-cirkels van de driehoeken ABC en BCD en de middens M_i van de zijden van de vierhoek.
U is het midden van AC, V is het midden van BD.
N is tweede snijpunt van de Euler-cirkels.

figuur 5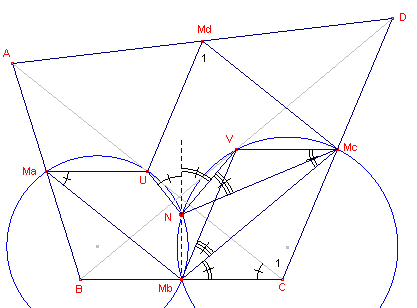

We zullen aantonen, dat ook N, V, M_b en M_c conclyclisch zijn (dus dat ze liggen op de Euler-cirkel van driehoek ACD).
M_aM_bNU is koordenvierhoek (Euler-cirkel).
Dus h(UM_aM_b) = buitenhoek bij N
MbMcVN is koordenvierhoek (Euler-cirkel).
Dus h(VM_cM_b) = buitenhoek bij N

MbCUM_a is parallelogram, dus h(UM_aM_b) = h(M_bCU).
VM_c // M_bC, dus h(VM_cM_b) = h(VM_bC).
h(VNMc) = h(VMbMc) staan op dezelfde boog.
CM_cM_dU is een parallellelogram, dus
h(C₁) = h(M_d1).

In parallellogran M_bCM_cV is h(C) + h(M_b) =180�.
Dus in vierhoek UNMcMd is h(N) + h(M_d) = 180�.
UNM_cM_d is dus een koordenvierhoek, waaruit volgt, dat N ook op de Euler-cirkel van de diagonaaldriehoek ACD van de vierhoek ligt.
Op dezelfde manier bewijzen we dat N ook op de Euler-cirkel van de diagonaaldriehoek ABD ligt.
Hier is stelling 2 bewezen. �

2.2. Koordenvierhoek
Indien de punten A, B, C, D hoekpunten zijn van een koordenvierhoek hebben we (zie figuur 6):

figuur 6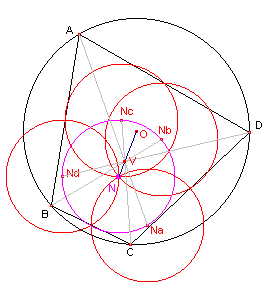

Stelling 3
De middelpunten van de Euler-cirkels van de diagonaaldriehoeken van een koordenvierhoek zijn conclyclisch met als middelpunt het punt van Euler van de vierhoek.

Bewijs:
Voor het bewijs van deze stelling wordt verwezen naar de pagina "Koordenvierhoeken", stelling 4. �

Opmerking
Het punt V is het centrum van vermenigvuldiging.
[einde Opmerking]

3. Euler-cirkels in een koordenvijfhoek
In figuur 7 staan de middelpunten 1',2',3',4' van de Euler-cirkels van de diagonaalvierhoeken van een koordenvijfhoek 12345.

figuur 7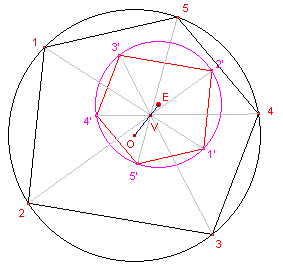

De Euler-cirkels van de diagonaalvierhoeken zijn voor de duidelijkheid uit de figuur weggelaten.
Op overeenkomstige manier als bij Stelling 3 kan het bewijs worden geleverd.

Opmerking
We kunnen eea. op dezelfde manier voortzetten voor koorden-n-hoeken met n = 6, 7 , 8, ...
[einde Opmerking]

Opmerking
Zie ook de pagina "Complexe getallen en meetkundige bewijzen - 4".
Daar wordt een bewijs gegeven van het bovenstaande met behulp van complexe getallen.
[einde Opmerking"

4. Samenhang met een orthogonale hyperbool
We bewijzen nu:

Stelling 4
Het Euler-punt van een vierhoek ABCD is het middelpunt van de orthogonale hyperbool door de punten A, B, C en D.

figuur 8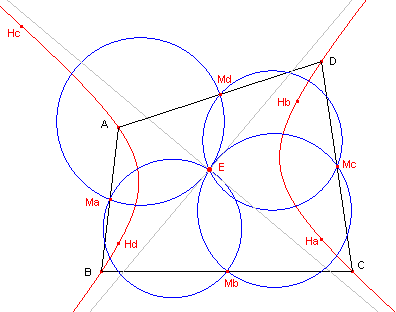

We gebruiken voor het bewijs van stelling 4 de volgende stelling:

Stelling 5
[1]
Als een orthogonale hyperbool door de hoekpunten van een driehoek gaat, dan ligt het middelpunt van die hyperbool op de cirkel van Euler van de driehoek.
[2]
Het hoogtepunt van de driehoek ligt op de hyperbool.

Opmerkingen
[1]
Stelling 5 is als probleem door Poncelet (Jean Victor Poncelet, 1788-1867, Frankrijk) en Brianchon (Charles Julien Brianchon, 1785-1864, Frankrijk) geformuleerd en wordt daarom ook wel aangegeven met Stelling van Poncelet-Brianchon.
Nb.
� Op de pagina "Probleem van Poncelet-Brianchon" wordt een ander analytisch bewijs van Stelling 5.2 gegeven dan hieronder is vermeld
� Op de pagina "Orthogonale hyperbool en driehoek" staat een projectief bewijs van Stelling 5.
[2]
De hyperbool wordt ook wel de hyperbool van Kiepert van driehoek ABC genoemd (naar Ludwig Kiepert, 1846-1934, Duitsland).
Zie de pagina "Probleem van Lemoine" waarop de hyperbool gegenereerd wordt met gelijkbenige driehoeken op de zijden van een driehoek.
[einde Opmerkingen]

Bewijs van Stelling 4:
Volgens Stelling 5 ligt het middelpunt van de hyperbool op elke Euler-cirkel van de diagonaaldriehoeken van de vierhoek.
Volgens Stelling 2 gaan deze Euler-cirkels door ��n punt, het Euler-punt van de vierhoek.
En daarmee is Stelling 4 bewezen. �

Dan nu het
Bewijs van Stelling 5
We gaan daarbij uit van een orthogonale hyperbool waarvan de assen samenvallen met de co�rdinaatsassen (zie figuur 9).

figuur 9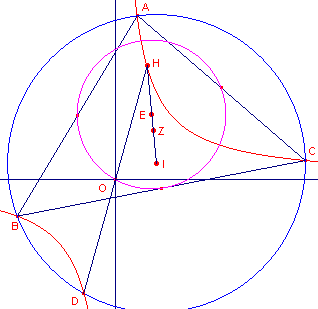

Getekend zijn de omgeschreven cirkel van driehoek ABC die de hyperbool in een vierde punt D snijdt.
En verder de punten I (incentrum), Z (zwaartepunt), E (Euler-punt) en H (hoogtepunt) en de Euler-cirkel van de driehoek.
We bewijzen nu met behulp van de analytische meetkunde.
De vergelijking van de hyperbool kunnen we schrijven als
xy = k
De vergelijking van de omgeschreven cirkel van driehoek ABC zij
x² + y² -2px - 2qy + r =0
Het middelpunt I heeft dus de co�rdinaten (p,q).

De x-co�rdinaten van de snijpunten van beide kromme volgen dan uit:

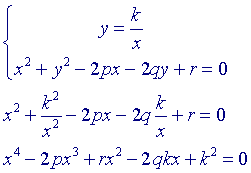
Voor de x-co�rdinaten x_i van de snijpunten hebben we dus: x₁+x₂+x₃+x₄ = 2p (co�ffici�nt van x³).
Voor de y-co�rdinaten y_i vinden we op dezelfde manier: y₁+y₂+y₃+y₄ = 2q.
Dus, vectori�el geschreven:
   OA + OB + OC + OD = 2OI.
   3OZ + OD = 2OI ...... (1)
Verder is 3IZ = IH, waarbij IZ = OZ - OI en IH = OH - OI.
Zodat
   3OZ - 3OI = OH - OI
waaruit
   3OZ - OH = 2OI ...... (2)
Uit (1) en (2) volgt dan OD = - OH.
Omdat D op de hyperbool ligt en deze spiegelsymmetrisch is in O, geldt dus ook:

Stelling 5.2: Het hoogtepunt H van de driehoek ligt op de hyperbool.

Uit HI = 2HE volgt dan, dat de Euler-cirkel uit de omgeschreven cirkel onstaat door de vermenigvuldiging d met factor � en centrum H.
Daarbij is d(D) = O.
Het punt O, het middelpunt van de hyperbool, ligt dus op de Euler-cirkel.
Hiermee is stelling 5.1 ook bewezen. �

Gevolg van Stelling 5.1
Ook de hoogtepunten van de diagonaaldriehoeken H_a, H_b, H_c en H_d liggen op de orthogonale hyperbool (zie figuur 10).

figuur 10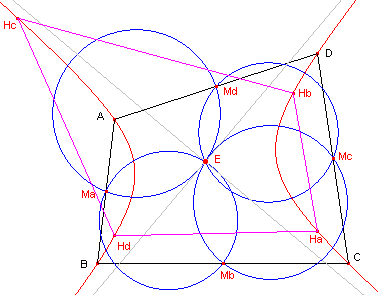

De hoekpunten van de diagonaaldriehoeken liggen immers op de orthogonale hyperbool.

[einde Gevolg]

[euler.htm] laatste wijziging op: 25-05-05