Probleem van Poncelet-Brianchon
Formulering | Oplossing | Referentie ][ Euler-cirkels | Meetkunde
1. Formulering van het probleem
Bepaal de meetkundige plaats van de hoogtepunten van de driehoeken die kunnen
worden beschreven in een orthogonale hyperbool.
2. Oplossing van het probleem
We kiezen na schaling de orthogonale hyperbool met vergelijking
xy = 1
Zij nu PQR een willekeurige driehoek die beschreven is in de hyperbool; dwz. PQR is een
driehoek waarvan de hoekpunten op de hyperbool liggen.
| figuur 1 |
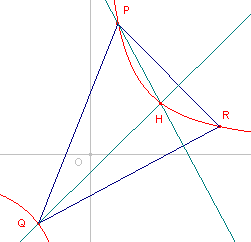 |
Stel de x-co�rdinaten van de punten P, Q, R zijn opvolgend a,
b, c.
De y-co�rdinaten zijn dan (in dezelfde volgorde) A = 1/a,
B = 1/b, C = 1/c.De richtingsco�ffici�nt van de zijde QR is dan
(B-C)/(b-c), of als we B en C vervangen:
(1/b - 1/c) / (b-c) = -1/bc.
De richtingsco�ffici�nt van de hoogtelijn op QR is dan bc.
Op basis hiervan is een vergelijking van deze hoogtelijn:
y - A = bc(x - a) |
Of verder uitgewerkt:
y + abc = bcx + A
y + abc = bc(x + A/bc)
y + abc = bc(x + ABC) ...... (1)
Op eenvoudige manier is uit (1) de vergelijking van de hoogtelijn op PR af te leiden:
y + abc = ac(x + ABC) ..... (2)
De co�rdinaten van het hoogtepunt H (we stellen ze x' en y') voldoen nu
aan de vergelijkingen (1) en (2).
Gelijkstelling van de rechter leden geeft dan eenvoudig voor de x-co�rdinaat van H:
x' = - ABC ...... (3)
Voor de y-co�rdinaat van H geldt dan:
y' = - abc ...... (4)
Vermenigvuldiging van (3) en (4) geeft dan x'y' = 1.
De co�rdinaten van het punt H voldoen dus aan de vergelijking xy = 1.
Met andere woorden:
De meetkundige plaats van de hoogtepunten van driehoeken die ingeschreven zijn in een
orthogonale hyperbool, is die orthogonale hyperbool zelf. �
Opmerkingen
[1]
Op de pagina "Euler-cirkels" is het probleem
geformuleerd als (Stelling 5 op die pagina):
[5.1]
Als een orthogonale hyperbool door de hoekpunten van een driehoek gaat, dan ligt het
middelpunt van die hyperbool op de cirkel van Euler van de driehoek.
[5.2]
Het hoogtepunt van de driehoek ligt op de hyperbool. |
[2]
Op de pagina "Orthogonale hyperbool en
driehoek" staat een projectief bewijs van de eigenschappen 5.1 en 5.2.
[3]
Een eerste oplossing van het probleem komt voor in
Annales de Gergonne, vol. XI, 1820-1821
Dit is een in 1810 door Joseph Diaz Gergonne (1771-1859, Frankrijk) gestart
wiskundig tijdschrijft.
3. Referentie
H. D�RRIE, 100 Great Problems of Elementary
Mathematics, Dover Publcations, New York, 1965

[poncbrian.htm] laatste wijziging op:
18-01-18
