Cabri-werkblad - Zwaartepunten

Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Het zwaartepunt van een veelhoek

Zwaartepunt van een lijnstuk
Zwaartepunt van een driehoek
Opdracht 1
Opdracht 2
Zwaartepunt van een vierhoek
     Opdracht 3
     Opdracht 4
     Opdracht 5
Naschrift
Opdracht 6 (facultatief)
Download

1. Zwaartepunt van een lijnstuk

We gaan uit van twee punten A₁ en A₂^:

figuur 1

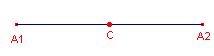Het midden van het lijnstuk A₁A₂ noemen we in dit geval ook wel het zwaartepunt van het lijnstuk.
We kunnen het punt C opvatten als centrum van een vermenigvuldiging met factor -1 waardoor het punt A₁ wordt afgebeeld op het punt A₂.

2. Zwaartepunt van een driehoek

figuur 2

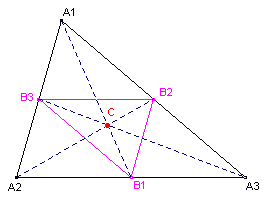De zwaartepunten (middens) van de zijden van een driehoek vormen een nieuwe driehoek.
Deze nieuwe driehoek is gelijkstandig met de oorspronkelijke driehoek (gelijkstandig betekent onder andere, dat de overeenkomstige zijden evenwijdig zijn).
Het centrum C van de bijbehorende vermenigvuldiging heet zwaartepunt van de driehoek.
De vermenigvuldigingsfactor van driehoek ABC tov. C is -�.

Opdracht 1

figuur 3

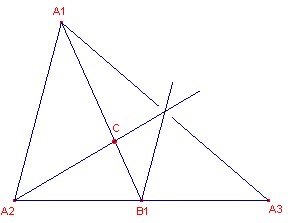Ga uit van driehoek A₁A₂A₃.

Bepaal het midden B₁ van A₂A₃. Kies het punt C op A₁B₁ zodat
A₁C : B₁C = 2 : 1
(kijk eens op het werkblad "Kromme van Koch (opdracht 1)" hoe je dat kan doen).

Bewijs nu, dat het beeld van het punt A₂ bij vermenigvuldiging ten opzichte van C met de factor -� samenvalt met het midden van A₁A₃.

Voer deze vermenigvuldiging, en ook die voor het punt A₃, met Cabri uit.

Aanwijzing

Maak voor het bewijs gebruik van de eigenschappen van een lijnstuk en het beeld daarvan bij vermenigvuldiging en van de middenparallel van een driehoek.
Opdracht 2
We maken vervolgens een macro waarmee het zwaartepunt van een driehoek kan worden geconstrueerd.
We hebben hierbij maar twee zwaartelijnen van de driehoek nodig.

Begin met een nieuw Cabri werkblad en teken daarop driehoek PQR (of je dat met lijnstukken of direct met behulp van de opdracht "Driehoek" in het Teken-menu doet, is niet van belang).
Teken de zwaartelijnen van de zijden PR en QR, en bepaal hun snijpunt C: het zwaartepunt van de driehoek.

Kies nu "Beginobjecten" in het Macro-menu.
Selecteer nu de hoekpunten van de driehoek.

figuur 4

Kies nu "Eindobjecten" in het Macro-menu.
Selecteer het zwaartepunt van de driehoek.
En kies tenslotte "Definieer macro" in het Macro-menu.
Maak daarin de aanvullingen als in de figuur hiernaast en klik op de knop OK.

Eventueel kan je de macro opslaan in een bestand. Hiervoor moet je de optie "Opslaan in bestand" aanklikken, zoals ook in de figuur hiernaast (figuur 4) is gedaan.
We zullen van deze macro gebruik maken in Opdracht 3.

3. Zwaartepunt van een vierhoek
In de volgende opdracht volgt zullen we het zwaartepunt van een vierhoek construeren.
Opdracht 3

Kies in Cabri een nieuw werkblad en teken een willekeurige vierhoek A₁A₂A₃A₄.

Teken daarin ook de diagonalen A₁A₃ en A₂A₄ (het tekenen van de diagonalen is voor de constructie echter niet van belang).

Ga na, dat je in vierhoek A₁A₂A₃A₄vier driehoeken kan bepalen, waarvan telkens ��n hoek samenvalt met (gelijk is aan) een hoek van de vierhoek. Van die hoek is de overstaande zijde dan een diagonaal van de vierhoek.
Welke zijn die vier driehoeken?

Gebruik de macro "zw3" (uit Opdracht 2) om van deze driehoeken de zwaartepunten B₁, B₂, B₃, B₄ te tekenen.

figuur 5

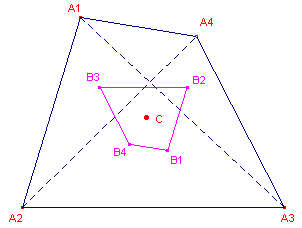Wat valt je nu op aan de vorm van vierhoek B₁B₂B₃B₄ als je die vergelijkt met de vorm van vierhoek A₁A₂A₃A₄?

Er is sprake van vermenigvuldiging (kan je dat bewijzen?). Met welke factor is er vermenigvuldigd?

Construeer het centrum van de vermenigvuldiging door de overeenkomstige punten (punt en beeldpunt, zoals A₁ en B₁) te verbinden.

Het gevonden punt is het zwaartepunt van vierhoek A₁A₂A₃A₄.

Hoeveel paren overeenkomstige punten moeten verbonden worden om het zwaartepunt van de vierhoek te vinden?

Opdracht 4

Maak een macro (noem deze "zw4") waarmee je het zwaartepunt van een vierhoek kunt tekenen. Doe dat op dezelfde manier als bij "zw3"; zie Opdracht 2. Neem bij het selecteren van de vier hoekpunten de juiste volgorde in acht!
Opdracht 5

Construeer het zwaartepunt van een vijfhoek (eventueel ook een zeshoek, ...).

Met welke factor is er in dit geval (deze gevallen) vermenigvuldigd?

4. Naschrift
De Engelse vertaling van "zwaartepunt" is "centre of gravity". Vaker wordt hiervoor in Engelse wiskunde-literatuur echter het woord "centroid" (Nederlands: centro�de) gebruikt.

Het gebruik van het woord "centroid" in Engelse literatuur is in een enkel geval verwarrend, als het gaat om (de definitie van) het zwaartepunt van een vierhoek.

In onderstaande figuren staan punten van een vierhoek die in Engelse wiskunde-literatuur ook met "centroid" worden aangegeven.

figuur 6

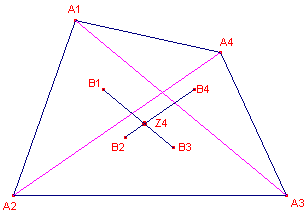In figuur 6:
De punten B1, B₂, B₃ en B₄ zijn de zwaartepunten van de vier driehoeken die een hoek met vierhoek A₁A₂A₃A₄ gemeenschappelijk hebben.

Z₄ is een "centro�de" van A₁A₂A₃A₄.

figuur 7

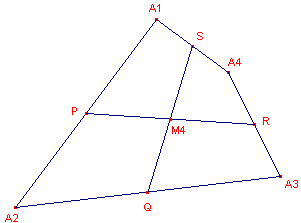In figuur 7:
P, Q, R en S zijn de middens van de zijden van vierhoek A₁A₂A₃A₄.
Definitie:

De verbindingslijnstukken van de middens van de overstaande zijden snijden elkaar in een punt dat centro�de (M₄) van de vierhoek wordt genoemd.

Opdracht 6 (facultatief)

Onderzoek onder welke voorwaarden het punt Z₄ samenvalt met het punt C (het in het werkblad gedefinieerde zwaartepunt van A₁A₂A₃A₄).

Onderzoek of het punt M₄ steeds samenvalt met het punt C.

5. Download
De Cabri-figuren op deze pagina zijn in ��n bestand via deze website te downloaden.
In dat bestand zijn ook enkele Cabr-macro's en een paar niet behandelde figuren opgenomen.
Klik hier om het downloaden te starten [ZIP-bestand, ca. 18Kb].

Van deze pagina is ook een PDF-versie beschikbaar:
zwaartep.pdf [ca. 43Kb].

[zwaartep.htm] laatste wijziging op: 23-03-2000