Meer over isogonale verwantschap
Overzicht ][ Isogonale verwantschap | Meetkunde
Zie ook de pagina "Isogonale verwantschap, ..."
1. Inleiding
![]()
Enkele van onderstaande eigenschappen is reeds vermeld op de pagina "Isogonale verwantschap, ...". De bewijzen van de stellingen op
deze pagina zijn echter meer met elkaar in overeenstemming gebracht.
We beginnen met (Stelling 2 van de pagina "Isogonale
verwantschap,..."):
| Stelling 1 Zijn l en m isogonaal verwant tov. hoek S(p,q), en zijn P en Q punten op opvolgend l en m, dan is het product van de beide afstanden tot p gelijk aan het product van de beide afstanden tot q. |
| Stelling 2 De vier projecties op de benen van een hoek van twee punten gelegen op twee isogonalen van die hoek zijn concyclisch. |
Bewijs:
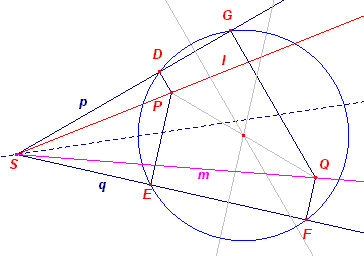 |
We hebben in nevenstaande figuur twee paar gelijkvormige rechthoekige
driehoeken: SQF, SPD en SQG, SPE Hieruit vinden we: SF : SD = SQ : SP = SG : SE Of SE � SF = SD � SG Waaruit het gestelde volgt (macht van S tov. de omcirkel van DEFG). � |
| Gevolg (van Stelling)
2 Het middelpunt van de cirkel is het midden van PQ. |
Bewijs:
Het middelpunt van de cirkel ligt op de middelloodlijn van DG en op de middelloodlijn van
EF. Deze lijnen gaan beide door het midden van PQ (middenparallel in het trapezium PDGQ en
in het trapezium PEFQ). �
| Stelling 3 De zes projecties van twee isogonaal geconjugeerde punten tov. een driehoek op de zijden van die driehoek zijn concyclisch. Het middelpunt van de cirkel ligt midden tussen beide isogonale punten. |
Bewijs:
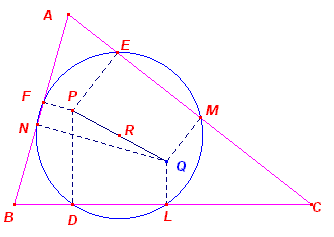 |
Volgens Stelling 2 (en het Gevolg van
Stelling 2) hebben we drie koordenvierhoeken: FNME, FNDL en DLME Het middelpunt van de omcirkel van elk van deze vierhoeken is telkens het punt R. Uit RF = RD = RM volgt dat deze drie cirkels samenvallen. �
|
| Stelling 4 Twee isogonale punten tov. een driehoek zijn de middelpunten van de cirkels door de spiegelbeelden van het bijbehorende isogonale punt in de zijden van die driehoek. |
Bewijs:
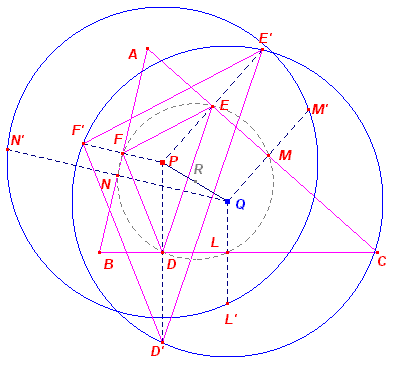 |
D,E,F zijn de projecties van P op de zijden; D', E', F' zijn de
gespeigeleden van P in de zijden. DEF en D'E'F' zijn gelijkstandige driehoeken, met centrum P; de factor is gelijk aan 2 (cq. �). R is het middelpunt van de omcirkel van DEF; Q is het middelpunt van de omcirkel van D'E'F'. Nu geldt PR : PQ = 1 : 2, dus Q ligt symmetrisch met P tov. R. Q is dus het isogonaalbeeld van P. � |
We bewijzen nu eerst een Hulpstelling over cirkelbundels.
Bewijs:
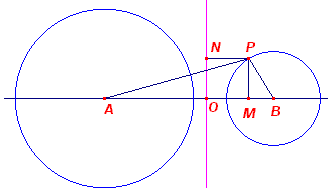 |
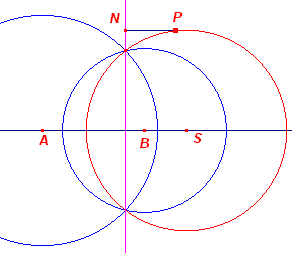
We bewijzen eerst (zie de figuur hiernaast) voor een punt P van een
cirkel (B, b), dat m(P, A) = 2NP � AB waarbij N het voetpunt is van de loodlijn uit P op de machtlijn van beide cirkels. Zij a de straal van cikel A. Nu is m(O,A) = m(O, B) = OA2 - a2 = OB2 - b2, zodat OA2 - OB2 = a2 - b2 Nu is (met M het voetpunt van de loodlijn uit P op de centraal): |
 |
[1] Zijn nu A en B twee cirkels die dienen als basiscirkels voor een cirkelbundel. Zij S een cirkel uit deze bundel en P een punt op die cirkel. Dan is (volgens het bovenstaande): m(P,A) = 2NP � AS en m(P,B) = 2NP � BS Zodat: m(P,A) : m(P,B) = AS : BS en dit geldt duidelijk voor elk punt P van cirkel S. [2] Zij P een punt van de meetkundige plaats. Dan is het punt S eenduidig bepaald door bovenstaande verhouding. Is een van beide machten negatief, dan ligt het punt S op het lijnstuk AB. � |
| . |
| Stelling 6 Als twee isogonale punten (bij een driehoek) collineair zijn met het omcentrum van die driehoek, dan raakt hun voetpuntscirkel aan de negenpuntcirkel. |
Bewijs:
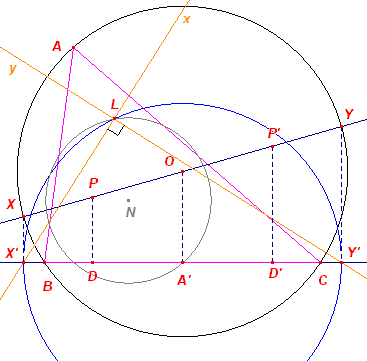 |
Als X, Y de eindpunten zijn van een middellijn van de omcirkel van ABC
dan staan de Simson-lijnen x en y van X en Y loodlrecht op elkaar en
ligt hun snijpunt L op de negenpuntcirkel. De projecties X', Y' van X, Y op BC liggen op x en y, en zijn symmetrisch tov. het midden A' van BC. Dus: de cirkel met middellijn X'Y' gaat door L. Zijn nu P en P' twee willekeurige
punten van XY. en zijn D, D' hun projecties op BC. Met R als straal van de omcirkel hebben
we dan: |
 |
Stel nu, dat P en P' isogonaal geconjugeerden zijn tov.
ABC. Volgens Stelling 3 liggen dan de zes projecties D, D', ... op een cirkel met middelpunt S (midden van PP'; ook liggend op XY). De producten A'D . A'D', ... zijn nu de machten van A', B', C' tov. de cirkel S. De uitdrukkingen (A'L)2, ... zijn de "machten" van A', B', C' tov. de puntcirkel L. Volgens Hulpstelling 5.2 en (eig) behoort nu de cirkel N tot de cirkelbundel bepaald door de cirkels S en L (immers A' ligt op cirkel N). Dus het punt N ligt op LS (de centraal van de bundel). Omdat L op de negenpuntscirkel N ligt, is de machtlijn van de bundel de raaklijn in L aan cirkel N. Cirkel S gaat dan ook door L en raakt dus in L aan cirkel N. � |
| . |
| Gevolg (van Stelling) 6 - Stelling van Feuerbach De incirkel en de uitcirkels van een driehoek raken aan de negenpuntcirkel. |
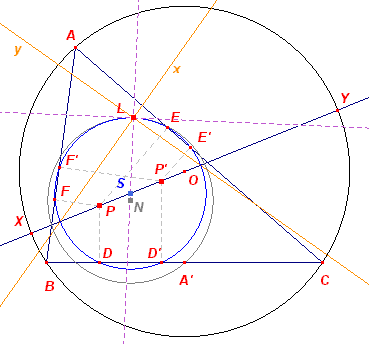
Bewijs:
 |
I zij het incentrum van driehoek ABC. Valt P samen met I (of met de uitcentra Ia, Ib of Ic), dan valt P' ook samen met I (of met de uitcentra). De punten D, D', ... vallen dus ook samen. Cirkel S is dan de incirkel van de driehoek en deze raakt dus aan de negenpuntcirkel (analoog voor de uitcirkels van ABC). � Gevolg Zie voor het Feuerbach-punt ook de pagina "Oppervlakte van voetpuntsdriehoeken". [einde Gevolg] |
Opmerking
De Stelling van Feuerbach is ook bewezen op de volgende pagina's:
- De Stelling van Feuerbach
- Complexe bewijzen (5)
- Inversie en de Stelling van Feuerbach
[einde Opmerking]
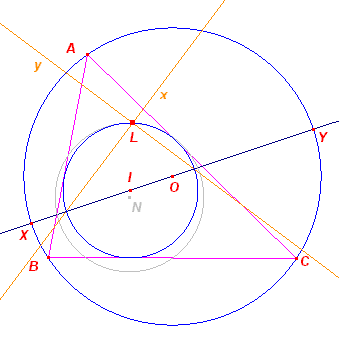
| Hulpstelling 7 De lijn door twee projecties van een punt op de benen van een hoek staat loodrecht op geconjugeerde van de lijn die dat punt met het hoekpunt verbindt. |
Bewijs:
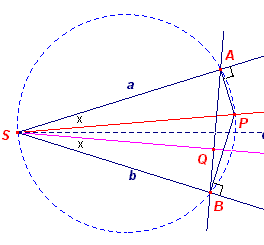 |
De projecties van P op de benen van hoek S zijn A en B. Vierhoek SBPA is dan een koordenvierhoek. Hieruit zien we dat SPA = �bg(AS) = SBA De driehoeken SBQ en SPA hebben dus twee hoeken gelijk. De derde dus ook, zodat Q = A = 90�. � Opmerking |
 |
|
|||
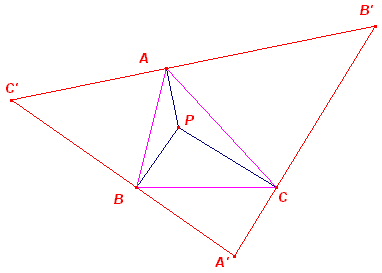
 |
Bewijs: A"B"C" is de antivoetpuntsdriehoek van Q; A'B'C' is de voetpuntsdriehoek van P. P en Q zijn isogonale punten. Volgens Hulpstelling 7 staat de drager
van B'C loodrecht op de isogonaal geconjugeerde van de lijn AP. |
|||
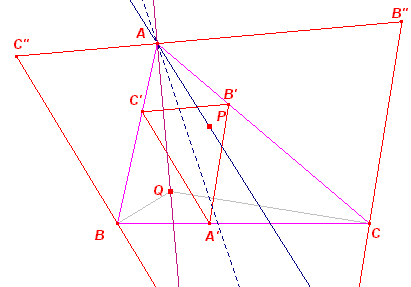
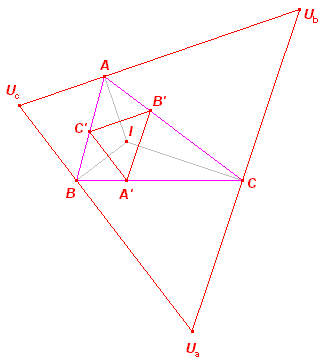 |
Voorbeelden [1] Zie de figuur hiernaast. De uitcentrum-driehoek UaUbUc van ABC is de antivoetpuntsdriehoek van het incentrum I. Aangezien I samenvalt met zijn isogonaal geconjugeerde, is de uitcentrum-driehoek homothetisch met de incentrum-driehoek van ABC (de voetpuntsdriehoek van I; Gergonne-driehoek). [2] |
| . |
| Stelling 9 Zijn P en Q twee isogonale punten tov. driehoek ABC, is verder D de oppervlakte van ABC, D1 de oppervlakte van de voetpuntsdriehoek A'B'C' van P en D2 de oppervlakte van de antivoetpuntsdriehoek A"B"C" van Q, dan geldt D1 . D2 = D2 (William Gallatly, The Modern Geometry of the Triangle, Hodgson, London, 1910-1st edition, pp.29-30) |
Opmerking
Clark Kimberling noemt deze Stelling (zonder bewijs, maar als een "an
interesting theorem") op pg. 188 van zijn boek Triangle Centers and Central
Triangles (Winnipeg, 1998).
[einde Opmerking]
Klik hier >![]() <
voor een CabriJavapplet die deze stelling illustreert.
<
voor een CabriJavapplet die deze stelling illustreert.
Zie de pagina "Voetpuntsdriehoeken" voor een
algemene behandeling van de oppervlakte van voetpuntsdriehoeken.
We bewijzen allereerst en algemeen:
Bewijs:
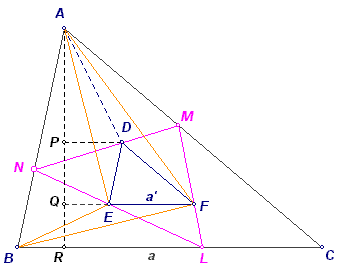 |
Teken het lijnstuk AD. Wegens DE // AB is dan O(DEN) = O(DEA). Evenzo geldt: O(DFM) = O(DFA) en O(EFL) = O(EFB) Dus: O(LMN) = O(AEBFA), immers DEF is deel van beide. Nu is O(AEBFA) = O(AEF) + O(BEF) DP // EQ // BC met P en Q op de hoogtelijn AR uit A. Zij nu AQ = u, QR = v, PQ = h' en AR = h = u + v Zij verder EF = a' en BC = a Dan is O(AEF) = � . u . a' en O(BEF) = � . v . a' |
Wegens de gelijkvormigheid geldt: h' : h = a' : a ...... (2)
En voorts: O2 = O(DEF) = � . h' . a'
Zodat O2 / O = h' / h ...... (3)
Uit (1), (2), (3) volgt dan: O / O1 = O2 / O, ofwel: O2
= O1 . O2 �
Gevolg (bewijs van Stelling 9)
Stelling 9 volgt direct uit Stelling 10,
immers A'B'C' en A"B"C" zijn gelijkstandig, terwijl ABC omgeschreven is om
A'B'C' en ingeschreven in A"B"C" (zie Stelling 8).�
Opmerking
We laten hier achterwege hoe we bij de gegeven configuratie van Stelling
10 de driehoek LMN moeten construeren.
[einde Opmerking]