Inleiding | Theorie | (Hi)story | Meer cirkels ][ Meetkunde
1. Inleiding
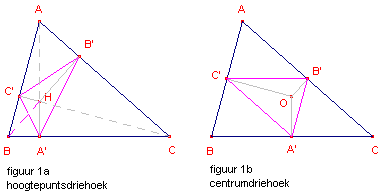
We kijken in deze paragraaf naar (zie figuur 1)
| [1] | de hoogtepuntdriehoek (voetpuntsdriehoek; de driehoek gevormd door de voetpunten van de hoogtelijn); |
| [2] | de centrumdriehoek (middelpuntsdriehoek; de voetpuntsdriehoek gevormd door de voetpunten van de loodlijnen uit het omcentrum van de driehoek). |
| . |
| figuur 1 |  |
Met de hoekpunten van de voetpuntsdriehoek(en) tekenen we cirkels:
| [1] | bij de hoogtepuntdriehoek gaan de cirkels door het omcentrum O; zie in figuur 2 (links) de cirkels A'(A'O), B'(B'O) en C'(C'O) |
| [2] | bij het omcentrum gaan de cirkeld door het hoogtepunt H; zie in figuur 2 (rechts) de cirkels A'(A'H), B'(B'H) en C'(C'H) |
De zes punten waarin deze cirkels de zijden van de driehoek snijden, liggen eveneens op een cirkel:
| [1] | bij de hoogtepuntdriehoek is het middelpunt van die cirkel het punt H; |
| [2] | bij de centrumdriehoek is het middelpunt van die cirkel het punt O. |
| . |
| figuur 2 | 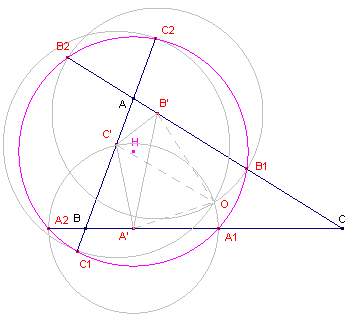 |
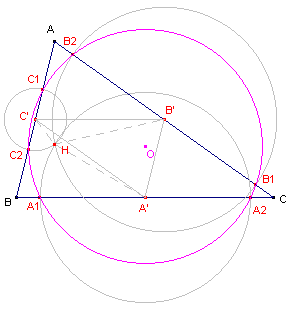 |
| [1] hoogtepuntdriehoek | [2] centrumdriehoek |
Klik hier ![]() voor een animatie
van het bovenstaande met CabriJava.
voor een animatie
van het bovenstaande met CabriJava.
De beide (laatste) cirkels heten cirkels van Droz-Farny (naar Arnold Droz-Farny, 1856-1912, Zwitserland).
Blijkbaar staan de beide Droz-Farny-cirkels wederzijds in verband met het hoogtepunt
H en het omcentrum O van een driehoek.
In paragraaf 2 geven we de theoretische achtergrond hiervan.
Zie ook Stelling op de pagina "Isogonale verwantschap, ..."
(en de daarbij behorende animatie).
| figuur 3 | 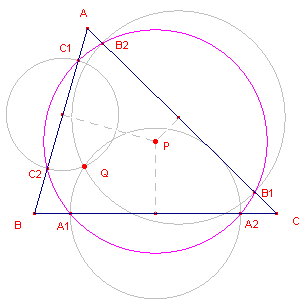 |
In figuur 3 is P een willekeurig punt. Het punt Q is het isogonaal geconjugeerde punt van P ten opzichte van de driehoek. P en Q zijn dus isogonaalpunten. Zie in dit verband de pagina "Isogonale verwantschap, ...", in het bijzonder Stelling 3 op die pagina. In de figuur zijn de voetpunten van de loodlijnen uit P op de zijden cirkels getekend die gaan door het punt Q. De snijpunten van deze cirkels met de zijden, A1, A2, B1, B2, C1, C2, liggen op een cirkel met middelpunt P. |
We kunnen algemeen formuleren:
| Stelling 1 (van Droz-Farny) Zijn P en Q isogonaalpunten van een driehoek, dan geldt: - de snijpunten van de zijden met de "voetpuntscirkels" van P die door Q gaan, zijn concyclisch met als middelpunt P; - de snijpunten van de zijden met de "voetpuntscirkels" van Q die door P gaan, zijn concyclisch met als middelpunt Q; - de beide Dros-Farny-cirkels hebben dezelfde straal. |
Voor het bewijs van de stelling van Droz-Farny maken we gebruik van onderstaande hulpstelling.
| Hulpstelling 1 - Isogonaaleigenschap De voetpuntsdriehoeken van twee isogonaalpunten hebben dezelfde omcirkel. |
Bewijs:
Het bewijs van deze stelling staat op de pagina "Isogonale verwantschap, ..." (als Stelling 3.2).
We geven hier echter een iets ander bewijs.
| figuur4 | 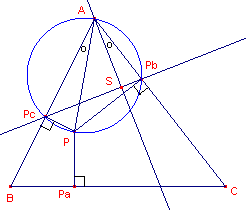 |
figuur 5 | 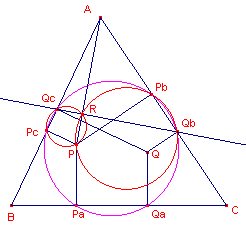 |
In figuur 4 vormen is APcPPb een koorden
vierhoek (twee overstaande rechte hoeken).
De isogonaal geconjugeerde van AP is de lijn die PbPc in het punt S
snijdt.
Nu is de hoek bij S gelijk aan 90� (isogonaaleigenschap).
Immers, �APPc + �PAPc
= 90�.
De hoeken APPc en APbS staan in de koordenvierhoek op dezelfde boog.
Dus �APPc = �APbS.
Maar ook �PAPc = �SAPb
(isogonale lijnen). We vinden dus:
�APbS + �SAPb
= 90�.
Zie nu figuur 5.
De punten Pa, Pb, Pc en Qa, Qb, Qc
zijn de voetpunten op de zijden van de isogonaalpunten P en Q.
Volgens de isogonaaleigenschap (zie eerste deel van dit bewijs) staat de lijn AP loodrecht
op QbQc (in het punt R).
Nu zijn PRQcPc en PRPbQb koordenvierhoeken.
We vinden daaruit (voor het punt A): AQc . APc
= AR . AP = ApB . AQb.
Zodat ook QcPcQbPb een koordenvierhoek is.
Voor het middelpunt M van de omcirkel van deze koordenvierhoek gebruiken we de
middelloodlijnen van de lijnstukken PbQb en PcQc.
Deze middelloodlijnen gaan beide door het midden van het lijnstuk PQ (middenparallel in
een trapezium).
M is dus het midden van PQ.
Op dezelfde manier bewijzen we dat PbQbQaPa
een koordenvierhoek is.
Ook van de omcirkel van deze vierhoek is M (het midden van PQ) het middelpunt.
De stralen van deze cirkels zijn gelijk (Pb, en ook Qb, ligt op
beide cirkels). �
Bewijs van de stelling van Droz-Farny
| figuur 6 | 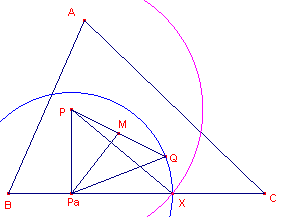 |
In figuur 6: - P en Q zijn isogonaalpunten van driehoek ABC - Pa is voetpunt van P op de zijde a - X is een snijpunt van de cirkel met middelpunt Pa die door Q gaat. We zullen nu de lengte van PX berekenen.
|
Zij nu u de lengte van het lijnstuk PQ (u is alleen afhankelijk van
de ligging van P).
Zij v de grootte van de straal van de voetpuntscirkel (= PaM) van het
paar P,Q (v is alleen afhankelijk van de ligging van P).
Dan is dus:
PX2 = �u2 + 2v2
PX is dus alleen afhankelijk van de ligging van P. Dus alle punten X,
zoals geconstrueerd, liggen op een cirkel met middelpunt P.
Wisselen we P en Q van rol, dan liggen ook alle punten die geconstrueerd worden met Q als
uitgangspunt, op een cirkel.
Beide cirkel hebben dezelfde straal.
Hiermee is de stelling van Droz-Farny bewezen. �
Klik hier ![]() voor een animatie
van het bovenstaande met CabriJava.
voor een animatie
van het bovenstaande met CabriJava.
Opmerking
De punten H en M van een driehoek zijn isogonaalpunten van de driehoek.
Voor het bewijs van deze eigenschap zie de Stelling (en de
animatie) op de pagina "Isogonale verwantschap, ..."
De eigenschappen die genoemd zijn in paragraaf 1, volgen immers direct
uit de Stelling van Droz-Farny.
[einde Opmerking]
3. (Hi)story
by Prof. Julio Gonz�lez Cabill�n, Uruguay
[Historia Matematica, V2 #134,
10-08-2000]
1. A close look in my personal library and databases showed that very little had been recorded of the life of the Swiss geometer A. Droz-Farny, other than the fact that he had lived in Porrentruy (Switzerland).
2. Then I decided to consult some old issues of Mathesis (Recueil math�matique, � l'usage des �coles speciales et des �tablissements d'instruction moyenne, published by P. Mansion & J. Neuberg) in which I located a short and uninformative obituary notice (in fact, two lines) on Droz-Farny. This note just recalled that Mathesis contributor Droz-Farny had recently passed away (volume for 1912), but nothing else.
3. It was not hard to assume that biographical information on Droz-Farny would not be
easy to locate from my off-track and down and under land. Therefore I decided to e-cross
the Atlantic Ocean, and e-knock on the doors of Porrentruy.
According the "Contr�le des habitants de la ville de Porrentruy", Arnold Droz,
son of Edouard & Louise, was born at La Chaux-de-Fonds, on February 12, 1856.
He married Lina n�e Farny, daughter of Constant & Anna, born also at La
Chaux-de-Fonds, on April 26, 1854. Arnold Droz died at Porrentruy on January 14, 1912.
An obituary was published in the newspaper "Le D�mocrate" (January 16, 1912)
which reads that he passed away after "une longue et p�nible maladie" ("a
long and painful disease").
Arnold had studied in the canton of Neuch�tel and in Munich before teaching "dans un
important institut de Suisse allemande" ("in an important institute of
German-speaking Switzerland").
In 1880, he was appointed professor of physics and mathematics at the cantonal School of
Porrentruy, where he taught until 1908.
I take this occasion to express to Fran�ois
Noirjean of the Archives
cantonales, Office du patrimoine historique (Porrentruy), and others who have replied
so openly, my warmest gratitude.
__________
Bovenstaande volgde op een vraag mijnerzijds via de Historia-Matematica-list (#128,
op 9-8-2000) naar de geboorte- en sterfdatum van Arnold Droz.
Op een vraag van een andere gebruiker van de Historia-Matematica-list naar hoe de
informatie was gevonden, het tweede deel van de (hi)story (V2 #132 (?), 21-08-2000).
����������
4. I looked on the Net for key-places in Porrentruy. As you know, you will always find
generous people on this bizarre planet who are willing to give you a helping hand.
Thus, one of my correspondents replied: "The appropriate recipient would be the Swiss
National Library (Schweizerische Landesbibliothek)".
When I dropped in there, another considerate soul responded: "After a quick look in
our catalogue, I can make an hypothesis about your first question, since an Arnold
Droz-Farny wrote 4 books between 1897 and 1909, two of them being on geometrical topics. I
forwarded your request to our Information Centre _IZ-Helvetica_, which will take care of
it and look for further details."
... And they surely took care of my issue, since a lovely answer came from Francois
Noirjean of the Archives cantonales (Office du patrimoine historique, CH-2900 Porrentruy).
I strongly believe that we (as a scholarly community) should be much more aware of the amazing power of the technologies of information.
Continuing the story
by Prof. Eduardo L. Ortiz, Mathematics Department, Imperial College, London
[Historia Matematica, V2 #137,
22-08-2000]
Arnold Droz-Farny is one of the many interesting characters in the history of the
geometry of the triangle, by the turn of the century. He was a teacher at Porrentruy,
Switzerland, near Basel.
All I know of his personal life is that he seems to have been very sociable, liked
mountain climbing and horse races, and kept correspondence with a number of
mathematicians, among them Virginio Retali in Italy, and Juan Jacobo Duran Loriga in
Spain. With the latter he kept correspondence between 1889 to 1910 when Duran Doriga died.
As Julio says, he died in 1912. In a letter of his I have read, he declared he studied
analysis with Klein (which possibly means he attended lectures by Klein), in Munich, but
preferred geometry.
4. Meer cirkels
Een bijzondere eigenschap wordt door Jakob Steiner (1796-1863, Zwitserland) vermeld en door Arnold Droz in
1901 ("Notes sur un th�or�me de Steiner"; in Mathesis, 22,
pag. 21-24) bewezen (zie Stelling 2).
| figuur 7 | 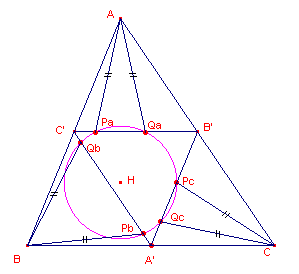 |
|
Bewijs: zie figuur 8.
| figuur 8 | 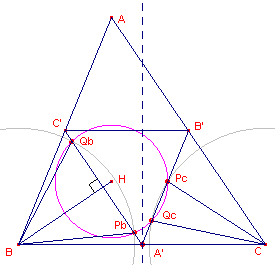 |
HB is deel van de hoogtelijn op AC en A'C'//AC, zodat HB loodrecht staat
op PbQb PbQb is koorde van de cirkel H, zodat BH middelloodlijn is van PbQb. Dus geldt BPb = BQb. Evenzo geldt: CPc = CQc. Voor de cirkels met middelpunten B en C die deze lijnstukken als straal hebben, geldt: A' ligt op de machtlijn van de cirkels H en B; A' ligt op de machtlijn van de cirkels H en C. A' ligt dus ook op de machtlijn van de cirkels B en C. De machten van A tov. de cirkels B en C zijn dus gelijk. |
Voor de macht van m(A', B) geldt: m(A',
B) = A'B2 - BPb2
Even zo is: m(A', C) = A'C2 -CPc2.
A'B = A'C zodat dus BPb = CPc.
Waarmee stelling 2 bewezen is. �
De omgekeerde stelling van Stelling 2 geldt ook:
| Stelling 3 Als de gelijke cirkels (met straal RABC) om de hoekpunten van een driehoek de zijden van de centrumdriehoek in paren punten snijden, dan liggen deze punten op een cirkel met middelpunt H. Voor de straal RH van die cirkel geldt: RH2 = 4R2 + RABC2 - �(a2 + b2 + c2) |
Bewijs:
We bewijzen hier alleen het tweede deel van de stelling (zie figuur 9).
| figuur 9 | 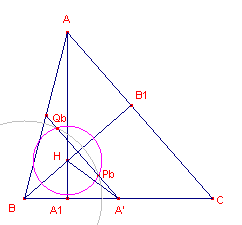 |
A' (het midden van BC) heeft gelijke machten m
tov. beide in figuur 9 getekende cirkels. m(A',B) = A'B2 - RABC2 m(A',H) = A'H2 - RH2 zodat RH2 = -�a2 + RABC2 + A'H2 ......(1) We berekenen nu A'H. |
In driehoek ABA1 is A1B = c . cosB
......(2)
In driehoek CB1B is B = 90�-C, zodat in driehoek A1HB geldt
tanB = cotC = A1H/A1B, waaruit A1H = c . cosB . cotC
......(3)
Met (2) en (3) vinden we dan voor A'H:
A'H2 = (�a - c . cosB)2
+ (c . cosB . cotC)2
Verder uitwerking hiervan (met gebruikmaking van sinus- en cosinusregel) geeft dan:
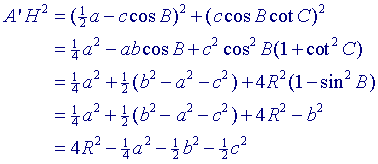
Dit geeft samen met (1):
RH2 = 4R2 + RABC2
- �(a2 + b2 + c2)
�
| figuur 10 | 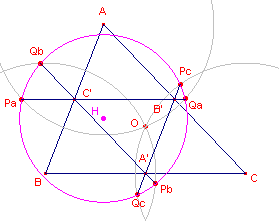 |
Kiezen we voor de gelijke cirkels om de hoekpunten de straal R (van de
omcirkel), dan gaan deze cirkels door O (het omcentrum; zie figuur 10). De straal RH van de cirkel om H is dan gelijk aan RH2 = 5R2 - �(a2 + b2 + c2). |
| figuur 11 | 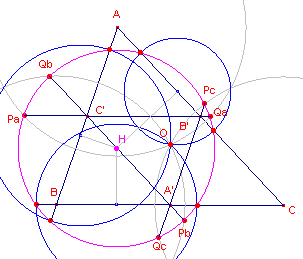 |
[2] In figuur 11 zijn ook de cirkels getekend van de hoogtepuntdriehoek, die door O gaan (zie paragraaf 1). Er blijk nu, dat de bijbehorende Droz-Farny-cirkel samenvalt met de Droz-Farny-cirkel die behoort bij de cirkels rond de hoekpunten (zie figuur 10). Op deze Droz-Farny-cirkel (de cirkel bij het hoogtepunt) liggen dus 12 bijzondere punten. We kunnen dit aantonen door de straal RH te berekenen van de Droz-Farny-cirkel bij het punt H (zie hieronder). |
[einde Gevolgen]
| Hulpstelling 2 HO2 = 9R2 - (a2 + b2+ c2) |
| figuur 12 | 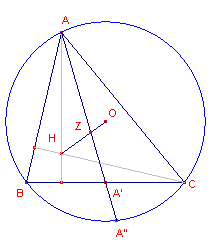 |
We bepalen de macht van het zwaartepunt Z tov. de omcirkel (O, R). We weten (zie de pagina "Cirkel van Feuerbach"), dat ZO = 1/3HO ......(1) Zij verder z de lengte van de zwaartelijn uit uit (AA'). De macht is gelijk aan ZO2 - R2 ......(2) maar ook
Voor A' geldt (koordenstelling): z . A'A" = 1/2a
. 1/2a = 1/4a2,
zodat |
En dan, met de zwaartelijnformule:
ZA . ZA" = -2/9(1/2b2
+ 1/2c2 - 1/4a2)
- 1/6a2 = -1/9(a2
+ b2 + c2)
Waaruit we via (2) vinden:
ZO2 = R2 -1/9(a2
+ b2 + c2)
en dan met (1)
HO2 = 9R2 - (a2 + b2+
c2)
�
We kunnen nu eenvoudig bewijzen:
| Stelling 4 Voor de straal RH van de Droz-Farny-cirkel bij het hoogtepunt (en van die bij het omcentrum) geldt: RH2 = 5R2 - �(a2 + b2 + c2). |
Bewijs:
In het bewijs van Stelling 1 hebben we gezien, dat voor RH
geldt:
RH2 = �u2
+ 2v2
waarbij nu u = HO en en v = de straal van de voetpuntscirkel van de
(isogonaalpunten) H en O.
De voetpuntscirkel van de punten H en O is de negenpuntscirkel. De straal daarvan is
gelijk aan �R (zie de pagina "Cirkel van Feuerbach").
Met hulpstelling 2 krijgen we dan
RH2 = �HO2 + 2(�R)2 = 4�R2 - �(a2
+ b2 + c2) + �R2,
dus
RH2 = 5R2
- �(a2 + b2 + c2)
waarmee Stelling 2 bewezen is.
�
Met Stelling 4 hebben we dus de bewering in Gevolg 2, met bijbehorende figuur 11, bewezen.