Overzicht ][ Inversie | Elementen | Meetkunde
Zie ook de pagina "Cabri: Euclidische passer en moderne passer"
1. Inleiding
![]()
Als Euclidische "werktuigen" worden bij meetkundige constructies alleen de
passer en de liniaal toegelaten.
De liniaal stelt ons in staat rechte lijnen door twee punten te tekenen.
De passer is in dit geval een werktuig dat met een gegeven middelpunt een cirkel kan
tekenen die door een punt gaat.
Opmerking
Wordt de Euclidische passer van het papier gelicht, dan klappen de benen onmiddellijk in.
Met een Euclidische passer is het dus niet mogelijk "afstanden over te brengen".
De "moderne" passer stelt ons echter in staat beide te doen.
We zullen hieronder laten zien, dat we "volgens Euclides zelf " de moderne
passer in Euclidische constructies mogen toepassen.
[einde Opmerking]
We vinden al direct in Boek I van de Elementen van Euclides (in vertaling van DR. E.J. DIJKSTERHUIS):
| Propositie I-1 Op een gegeven begrensde rechte een gelijkzijdigen driehoek te construeren. Propositie I-2 |
Opmerking
Euclides verstaat hier onder "rechte" wat wij "lijnstuk" noemen.
[einde Opmerking]
| figuur 1 | 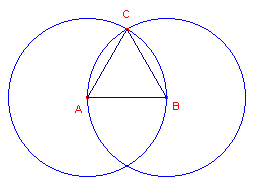 |
Bewijs van I-1: Postulaat 3 (Elementen Boek I) luidt: En dat met elk middelpunt en elke afstand een cirkel beschreven wordt. Op basis hiervan is het dus mogelijk cirkels te tekenen met middelpunt A en met middelpunt B, met straal AB. Euclides bewijst dan op grond van eerder gegeven postulaten en definities, dat AB = BC = CA. � |
| figuur 2 | 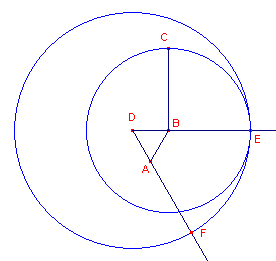 |
Bewijs van I-2: Zij A het gegeven punt en BC het gegeven lijnstuk. We moeten dan een lijnstuk construeren dat gelijk is aan BC, met A als beginpunt. Volgens I-1 kan op AB een gelijkzijdige driehoek ABD worden getekend. DA en DB kunnen worden verlengd (zie Postulaat 2). Postulaat 3 (zie boven in het bewijs van I-1) geeft ons de mogelijkheid tot het tekenen van cirkel B(BC), die de lijn DB in E snijdt. Cirkel D(DE) snijdt de lijn DA in F. Nu is AF = BC. � |
Merk op, dat in de bovenstaande cirkel-constructies alleen gebruik gemaakt is van een "Euclidische passer".
Propositie I-3 (Elementen) stelt ons nu in staat "afstanden over te brengen".
| Propositie I-3 Wanneer twee ongelijke rechten (lijnstukken, DK) gegeven zijn, van de grootere een rechte, gelijk aan de kleinere, af te nemen. |
Constructie:
| figuur 3 | 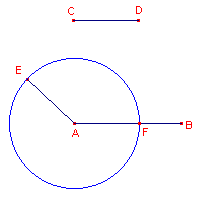 |
Zijn AB en CD de gegeven lijnstukken, waarbij AB > CD. We construeren het lijnstuk AE dat gelijk is aan CD (volgens Prop. I-2). Vervolgens snijdt de cirkel A(AE) het lijnstuk AB in het punt F. Nu is AF = CD. � Opmerking |
Gevolg
We kunnen de Euclidische passer vervangen door een "gewone" (moderne) passer.
| � | Klik hier voor de pagina "Cabri: Euclidische passer en moderne passer". Op deze pagina wordt eveneens ingegaan op de equivalentie tussen constructies met een Euclidische passer en een moderne passer. Ook komen op die pagina enkele Cabri-constructies en -macro's aan de orde. |
2.
Passermeetkunde ![]()
We zullen hieronder aantonen, dat we de liniaal niet nodig hebben bij de elementaire
Euclidische constructies.
| Definitie Een rechte lijn is het paar (A,B) waarbij A en B verschillende punten zijn in het Euclidische vlak. (A, B) wordt ook wel geschreven als AB. |
In deze definitie wordt de rechte lijn dus impliciet vast gelegd door twee punten. Elk
tweetal verschillende punten bepaalt daardoor een rechte lijn (die we niet hoeven te
tekenen).
Nodig is nu aan te tonen, dat we de liniaal kunnen missen bij penl-constructies (zie de
pagina "Trisectie").
De basisproblemen bij Euclidische constructies zijn:
| (i) | het vinden van de snijpunten van twee cirkels (elk gegeven door middelpunt en straal); |
| (ii) | het vinden van het snijpunt van een lijn (vastgelegd door twee verschillende punten; zie definitie hierboven) en een cirkel; |
| (iii) | het vinden van de snijpunten van twee lijnen (elk vastgelegd door twee verschillende punten). |
Ad (i)
De oplossing hiervan is onmiddellijk duidelijk. Dit kan zonder liniaal.
Ad (ii) en (iii)
We zullen aantonen (in Stelling 4), dat we (ii) en (iii) kunnen
terugbrengen tot (i) door inversie (zie voor Inversie de pagina "Inversie" en het Cabri-werkblad "Inversie").
Opmerking
De bewijsvoering met behulp van inversie is voor het eerst toegepast in 1890 door August
Adler (1863-1923) in zijn artikel "Zur Theorie der Mascheronischen Konstruktionen"
(Wiener Berichte Nr. 99).
[einde Opmerking]
We bewijzen eerst enkele hulpstellingen (stelling 1, stelling 2 en stelling 3).
| Stelling 1 Het is mogelijk met passer alleen het inverse punt P' van een punt P tov. van een cirkel O te construeren. |
| figuur 4 | 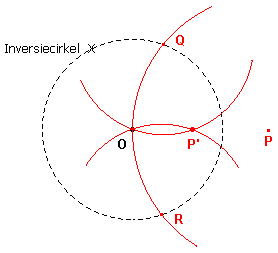 |
De volgende constructiestappen zijn voldoende (bij gegeven inversiecirkel
O en punt P):
De juistheid van de constructie volgt uit: |
Opmerking
Dit bewijs staat ook op de pagina "Inversie".
Daar staat eveneens een CabriJavapplet
die de constructie, zoals die in figuur 4, illustreert.
[einde Opmerking]
Bewijs:
| figuur 5 | 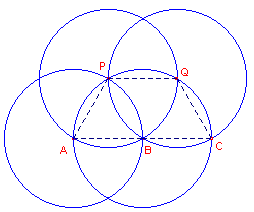 |
[1] Zij AB het gegeven lijnstuk (ook nu bepaald door de punten A en B). Teken de cirkel A(AB). Bepaal de cirkel A(AB) het punt P, dan met P(PA) het punt Q en tenslotte met Q(QP) het punt C. Nu is AC een rechte lijn, waarbij AB = BC. � |
| figuur 6 | 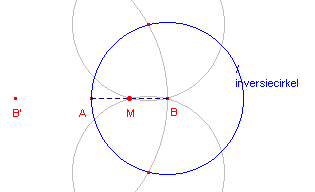 |
[2] Bepaal B' op BA zodat BA = AB', volgens Stelling 2.1. Bepaal de inverse M van B' tov. de cirkel B(BA), volgens Stelling 1. Nu is M het midden van AB. Immers, zij r (=AB) de straal van de inversiecirkel. Dan is: BM . BB' = BM . 2r = r2. Waaruit volgt dat BM = � r. � Klik hier |
| . |
| Stelling 3 Het is mogelijk met passer alleen het middelpunt van de cirkel door drie gegeven punten te construeren. |
| figuur 7a | 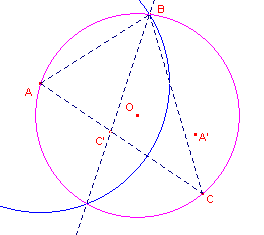 |
Zijn A, B, C drie gegeven punten (die niet op dezelfde lijn liggen). We kiezen de cirkel A(AB) als inversiecirkel. De omcirkel van ABC gaat door inversie over in de lijn BC' (C' is het beeld van C bij deze inversie). Het gezochte punt O gaat bij de inversie over in het inverse beeld van A bij de inversie tov. BC' (zie Toelichting). O gaat dus over in het spiegelbeeld A' van A in de lijn BC' (het spiegelbeeld A' van A is te construeren met de cirkels B(BA) en C'(C'A)). O is dus het beeld van A' bij de inversie in de cirkel A(AB). � Klik hier |
| figuur 7b | 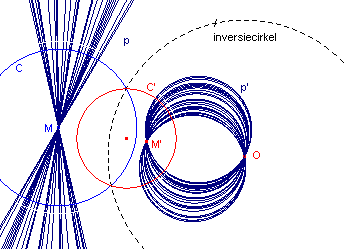 |
Zie figuur 7b. Alle rechte lijnen p door het middelpunt M van een cirkel C worden bij een inversie (tov. een cirkel met middelpunt O) afgebeeld op cirkels die door O gaan. Deze cirkelbundel heeft een tweede basispunt, namelijk het beeld M' van het punt M (bij de inversie tov. cirkel O). De cirkels van deze bundel staan alle loodrecht op het beeld C' van de cirkel C. We bekijken nu de inversie tov. de cirkel C'. De cirkels van de bundel worden nu afgebeeld op zichzelf (vanwege de orthogonaliteit). M' is dan het beeld van O bij de inversie tov. de cirkel C'. |
| figuur 7c | 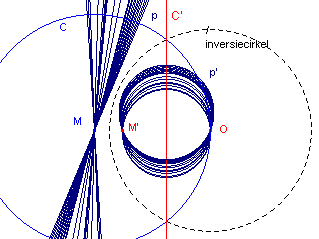 |
Zie nu figuur 7c. Ligt het punt O op cirkel C, dan is het beeld C' van C een rechte lijn. Het beeld M' van M ligt dan spiegelsymmetrisch tov. de rechte lijn C' . |
Opmerking
Bovenstaande levert ook een passer-constructie van het middelpunt van een cirkel.
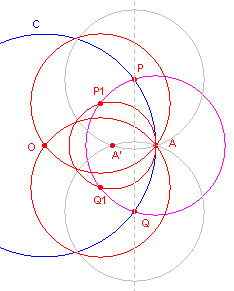
| figuur 7d | 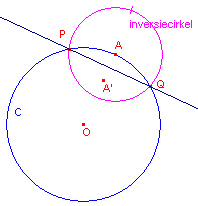 |
Zie figuur 7d. Zij C de cirkel waarvan het middelpunt onbekend is. Kies een willekeurig punt A op C, dat middelpunt is van een cirkel die C in de punten P en Q snijdt. A' is het beeld bij spiegeling van A in de lijn PQ. Dan is het beeld O van A' bij inversie in cirkel A het middelpunt van cirkel C. In de rechter figuur staat de hierop gebaseerde passer-constructie. [einde Opmerking] |
 |
We kunnen nu op basis van Stelling 3 bewijzen:
| Stelling 4 [1] Het is mogelijk met passer alleen de snijpunten van een lijn en een cirkel te construeren. [2] Het is mogelijk met passer alleen het snijpunt van twee lijnen te construeren. |
| figuur 8a | 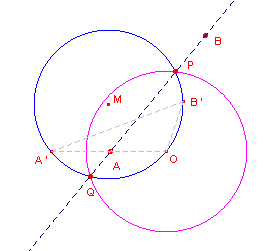 |
[1] We kiezen de cirkel (die de lijn AB snijdt) als inversiecirkel. A' en B' zijn de inversen van A en B tov die cirkel. De punten A' en B' zijn volgens Stelling 1 met passer te construeren. Het beeld van de lijn AB bij de inversie is de omcirkel van driehoek OA'B'. De snijpunten P en Q van AB met de inversiecirkel zijn invariant. P en Q zijn dus de snijpunten van de omcirkel van driehoek OA'B' en de inversiecirkel. Volgens Stelling 3 is het middelpunt M van die omcirkel met passer te construeren. De snijpunten zijn nu als snijpunten van de omcirkel en de inversiecirkel te construeren (zie figuur 8a).� Klik hier |
| figuur 8b | 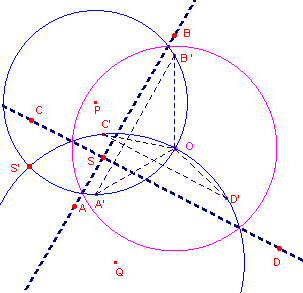 |
[2], zie figuur 8b. AB en CD zijn de gegeven lijnen. We kiezen een geschikte inversiecirkel O. A', B', C', D' zijn de inversen van A, B, C, D tov. deze cirkel. Het tweede snijpunt S' van de omcirkels van OA'B' en OC'D' (zie Stelling 3 voor de constructie van de cirkels P en Q) is het beeld van het snijpunt S van AB en CD.� Klik hier |
3. Mascheroni en
Mohr ![]()
Lorenzo Mascheroni (1750-1800, Itali�) publiceerde in
1797 in Pavia het werk Geometria del compasso. Hij toonde daarin, op een andere
manier als hierboven, aan dat iedere penl-constructie kon worden uitgevoerd met passer
alleen.
Hij stelde zich niet tevreden met het bewijs van de mogelijkheid, maar hij gaf daarnaast
een groot aantal interessante toepassingen op allerlei meetkundige problemen.
Ook gaf hij een aantal benaderde oplossingen (zie Paragraaf 4) van
constructies die met penl niet exact uit te voeren waren.
Het werk van Mascheroni werd vooral in Frankrijk bekend door toedoen van Napoleon. Tijdens
zijn Italiaanse veldtocht had hij Mascheroni ontmoet en hij raakte in diens werk
ge�ntereseerd (Geometria is door Mascheroni opgedragen aan Napoleon).
Bij terugkomst in Frankrijk woonde hij op 10 december 1797 een bijeenkomst bij van het
Institut National, waar ook Lagrange en Lapace aanwezig waren.
Naar het schijnt heeft hij hen een probleem (zie Voorbeeld 2)
voorgelegd en de passerconstructie gedemonstreerd.
Laplace, die Napoleon's leermeester was geweest op de militaire school in Brienne, sprak
toen: "Nous attendions tout de vous, g�n�ral, except� de le�ons de
math�matiques".
Een gevolg hiervan was weer dat, door de publiciteit in een Frans dagblad, zeer snel een
Franse vertaling werd verzorgd, G�om�trie du
compas, door A.M. Carette (verschenen in 1798 bij Duprat in Parijs; 2e
druk 1828).
Georg (J�rgen) Mohr (1640-1697, Denemarken) bracht een
groot deel van zijn leven in Nederland door. In 1672 (dus 125 jaar voor Mascheroni)
publiceerde hij Euclides Danicus (uitgegeven te Amsterdam in het Nederlands en in
het Deens), dat geheel aan de passermeetkunde was gewijd. Hij toonde daarin ook aan, zij
het meer theoretisch en minder eenvoudig dan Mascheroni, dat penl-constructies met passer
alleen mogelijk zijn.
Het boek werd bij toeval ontdekt door een student van de Deense meetkundige Johannes
Hjelmslev (1873-1950) en door de laatste als facsimile heruitgegeven in 1928 (mmv. det
Kgl. Danske Videnskabernes Selskab te Kopenhagen).
Klik hier voor oa. een levensbeschrijving
van Mohr in het Deens en een afbeelding van de eerste bladzijde van Euclides Danicus.
Voorbeelden ![]()
Hieronder geven we een viertal voorbeelden van de constructies van Mascheroni.
Voor een vijfde voorbeeld (met een afdruk uit G�om�trie du compas, op een afzonderlijke pagina):
[1] ![]()
Een gegeven cirkelboog te halveren
| figuur 9 | 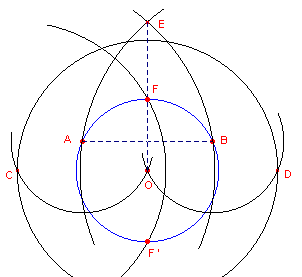 |
De koorde wordt bepaald door de punten A en B op de cirkel met middelpunt
O. We geven de constructiestappen kort weer. 1 - Cirkel(O, AB) 2 - Cirkel(A, O) ...... dit geeft snijpunt C 3 - Cirkel(B, O) ...... dit geeft snijpunt D 4, 5 - Cirkel(C, B) en Cirkel(D, A) ...... deze geven snijpunt E 6 - Cirkel(C, OE) ...... dit geeft de snijpunten F en F'. F en F' zijn punten die elk van beide bogen AB halveren.� |
[2] ![]()
Probleem van Napoleon - Een vierkant te construeren in een cirkel
Dit probleem vertoont uiteraard veel gelijkenis met dat in Voorbeeld 1.
| figuur 10a | 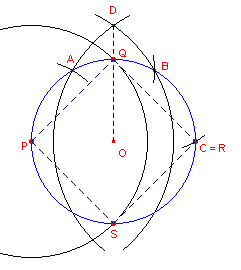 |
De cirkel met middelpunt O met daarop het punt P zijn gegeven. Constructiestappen: 1 - Cirkel(P, O) ...... dit geeft punt A 2 - Cirkel(A, O) ...... dit geeft punt B 3 - Cirkel(B, O) ...... dit geeft punt C = R 4, 5 - Cirkel(P, B) en Cirkel(C, A) ...... geven snijpunt D 6 - Cirkel(P, OD) ...... dit geeft de punten Q en S. PQRS is dan het gevraagde vierkant.� Klik hier
Opmerkingen |
| figuur 10b | 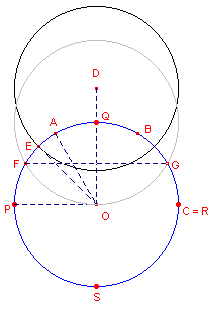 |
[2] Deze constructie biedt echter ook wat meer. Hebben we punt D eenmaal gevonden, dan kunnen we in de cirkel ook een regelmatige 24-hoek construeren. Constructiestap: 7 - Cirkel(D, OP) ...... dit geeft het punt E (het midden van bg PQ). Nu is bg AE = 60� - 45� = 15�. Het waren juist de constructies voor het verdelen van de cirkel in een aantal gelijk bogen, waarmee Mascheroni zijn onderzoek is begonnen. Nb. |
| figuur 10c | 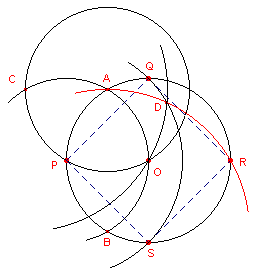 |
[3] - Tweede constructie In [1] is het vierkant geconstrueerd met 6 extra cirkels. Het is ook mogelijk de constructie uit te voeren met 5 extra cirkels (zie figuur 10c). Constructiestappen: 1 - Cirkel(P, O) ...... dit geeft de punten A en B 2 - Cirkel(B, A) ...... dit geeft punt R 3, 4 - Cirkel(A, O) en Cirkel(P, O) ...... geven het punt C 5 - Cirkel(C, O) en Xirkel(B, A) ...... geven het punt D 6 - Cirkel(P, D) ...... geeft de punten Q en S. Hierbij zij opgemerkt, dat alle gebruikte cirkels getekend zijn met een "Euclidische" passer. |
[3] ![]()
De middelevenredige te construeren bij twee lijnstukken
We voeren deze constructie, van wege de leesbaarheid, in delen uit.
De constructie is gebaseerd op de eigenschap dat in een rechthoekige driehoek het kwadraat
van de hoogtelijn op de schuine zijde gelijk is aan het produkt van de stukken waarin die
zijde door de hoogtelijn wordt verdeeld (h2 = pq).
| figuur 11a | 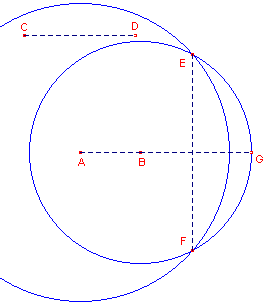 |
AB en CD zijn de gegeven lijnstukken. Allereerst moeten we AB verlengen met een lijnstuk ter lengte van CD. 1 - Cirkel(B, CD) 2 - snijdende Cirkel(A, willekeurige straal) Dit geeft de punten E en F. Het punt G wordt dan bepaald als midden van boog EF op cirkel 1 (zie hiervoor de constructie in Voorbeeld 1). |
| figuur 11b | 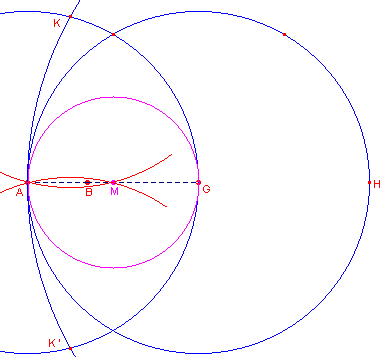 |
Vervolgens moet het midden van het lijnstuk AG worden geconstrueerd. Allereerst is AG verlengd met een stuk GH = AB. Zie hiervoor Stelling 2.1. 3 - Cirkel(A, AG) 4 - Cirkel(H, HA) Deze cirkels snijden elkaar in de punten K en K'. 5 - Cirkel(K, KA) 6 - Cirkel(K', K'A) Deze cirkels snijden elkaar in het punt M. M is nu het midden van AG. De cirkel met middellijn AG kan nu getekend worden. |
| figuur 11c | 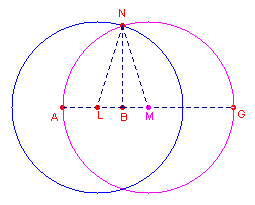 |
We spiegelen nu het punt M in B. Dit doen we door het lijnstuk MB met BL = MB te verlengen (ook weer volgens Stelling 2.1). 7 - Cirkel(L, AM) Deze snijdt cirkel M in het punt N. Nu is BN middelevenredig tussen AB en BG = CD. � |
[4] ![]()
Het construeren van het snijpunt van twee lijnen
In Stelling 4.2 hebben we laten zien hoe het snijpunt van twee
lijnen kan worden geconstrueerd met behulp van inversie.
We laten nu de constructie van Mascheroni hieronder volgen (zie de figuren
12a en 12b).
Een tweede, eenvoudiger, constructie wordt beschreven in de Opmerking
aan het eind.
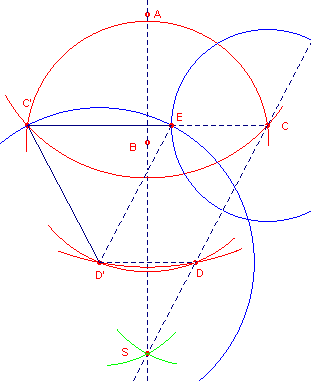
| figuur 12a | figuur 12b | |
 |
 |
We construeren eerst de spiegelbeelden C' en D' van C en D in AB (zie
figuur 12a, rode cirkels).
Vervolgens bepalen we het parallellogram DD'EC (D'E // CD; blauwe cirkels die het punt E
bepalen).
Nu geldt voor het, nu nog denkbeeldige, snijpunt S:
C'E : D'D = C'D' : D'S (gelijkbenige
gelijkvormige driehoeken) ------ (1)
We moeten nu het lijnstuk D'S als vierde evenredige construeren.
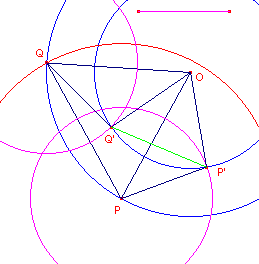
Dat doen we in figuur 12b.
Om O zijn cirkels (blauw) getekend met stralen C'E en D'D. Het punt Q wordt bepaald met de
cirkel P(C'D'), waarbij P een willekeurig punt op de cirkel is.
Met een willekeurige straal worden dan cirkels P en Q getekend die de punten P' en Q'
geven.
In de figuur hebben we dan: OP = C'E, OP' = D'D en PQ = C'D'.
Nu zijn de driehoeken OPP' en OQQ' congruent.
Dus zijn de beide gelijkbenige driehoeken OPQ en OP'Q' gelijkvormig (gelijke tophoeken).
Hieruit volgt dan: OP : PQ = OP' : P'Q',
of
C'E : C'D' = D'D : P'Q' ------
(2)
Uit (1) en (2) volgt dan dat P'Q' = D'S.
In figuur 12a construeren we dan S met de (groene) cirkels D(P'Q') en
D'(P'Q'). �
Opmerking - 2e constructie
Het is vreemd, dat Mascheroni voor de constructie van het snijpunt van de lijnen niet
doorgaat op het eerste deel van bovenstaande constructie, namelijk de
gebruikte lijnspiegeling.
Hieronder geven we een constructie waarbij drie keer gebruik gemaakt wordt van een
lijnspiegeling, met tenslotte voor de constructie van het snijpunt toepassing van Stelling 3 (middelpunt van de cirkel door 3 punten).
| figuur 13 | 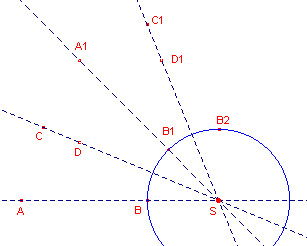 |
A1, B1 zijn de
beelden van A, B bij de spiegeling in de lijn CD. C1, D1 zijn de beelden van C, D bij de spiegeling in de lijn A1B1. B2 is het beeld van B1 bij de spiegeling in de lijn C1D1. Het product van deze spiegelingen is een rotatie om het snijpunt van de spiegelassen. De punten B, B1 en B2 liggen dus op een cirkel met als middelpunt het snijpunt van AB en CD. We kunnen dus volgens Stelling 3 het middelpunt van de omcirkel van driehoek BB1B2 construeren. � |
4.
Benaderingsconstructies van Mascheroni ![]()
Zoals reeds opgemerkt heeft Mascheroni ook een aantal benaderingsconstructies (met
passer alleen) gevonden van problemen die niet met penl kunnen worden opgelost.
We behandelen op deze website:
Bij oplossing van de eerste twee problemen maakt Mascheroni gebruik van een constructie die is terug te vinden in Voorbeeld 2.
Klik hier voor Mascheroni's benaderingsconstructies (met CabriJavapplets).
Zie verder eventueel de webpagina "Trisectie van een hoek".
Zie ook de pagina "Passermeetkunde:
Over Georg Mohr".
Zie ook de pagina "Passermeetkunde:
G�om�trie du compas".
Zie ook de pagina "Cabri:
Euclidische passer en moderne passer"
| [1] | A. BOGOMOLNY, Geometric construction with the compass alone (website van Cut-The-Knot, USA) | |
| [2] | H. D�RRIE, 100 Great Problems of Elementary Mathematics, Dover Publications, New York (1965) | |
| [3] | J-L. Juveneton, Cabri Java: construire avec le compas, (Acad�mie de Grenoble, Frankrijk) | |
| [4] | G.E. MARTIN, Geometric constructions, Springer-Verlag, New York (1998) | |
| [5] | D. PEDOE, Circles: a mathematical view, MAA, Washington (1995) | |
| [6] | S.C. VAN VEEN, Passermeetkunde, J. Noorduijn en Zoon N.V., Gorinchem (1951) | |
| [7] | HK. DE VRIES, Historische Studi�n, deel 1, P. Noordhoff, Groningen (1926) |
6. Download ![]()
De meeste Cabri-figuren op deze pagina kunnen in ��n bestand via deze website worden
gedownload.
In het bestand zijn ook de figuren opgenomen van de CabriJavapplets en die van de pagina
"Benaderingsconstructies".
Klik hier om het downloaden te starten (ZIP-bestand, ca. 25Kb).