Over de trisectie van een hoek
Zie eventueel ook: Een misvatting... (artikel, PDF-bestand, ca. 60Kb) en Daafs Gedachten - Trisectie.
1. Meetkunde
en algebra ![]()
Tot de meetkundige problemen die ook door de Grieken niet konden worden
opgelost (niet onbegrijpelijk, overigens), behoren
| ? | Trisectie van de hoek: | Gegeven een hoek, verdeel die hoek met behulp van passer en liniaal (we schrijven in hetgeen volgt "penl"). |
| ? | Verdubbeling van de kubus: | Gegeven een lijnstuk met lengte 1, construeer een lijnstuk met lengte 3?2 met behulp van penl (het zogenoemde "Delisch probleem"). |
| ? | Kwadratuur van de cirkel: | Gegeven een lijnstuk met lengte 1, construeer een vierkant met
oppervlakte p met behulp van penl. Dit proces heet ook wel 'kwadreren'. |
Deze drie problemen zijn inderdaad onoplosbaar (er is een verschil tussen "niet
kunnen oplossen" en "onoplosbaar").
Merk op dat dit niet wil zeggen dat er, blijvend bij het eerste onoplosbare probleem, geen
hoeken bestaan die (met behulp van passer en liniaal) in drie delen kunnen worden
verdeeld. Duidelijk is, dat dit zeker wel het geval is met de rechte hoek.
"Het trisectieprobleem van de hoek is onoplosbaar" wil zeggen, dat "er is
ten minste ??n hoek die niet met behulp van penl in drie gelijke stukken kan worden
verdeeld".
Voordat we het bewijs van de onoplosbaarheid van de eerste twee problemen leveren,
geven we eerst een enkele definitie en behandelen we een aantal stellingen die met die
definities samenhangen.
Bij onze beschouwingen gaan we uit van een plat vlak waarin een rechthoekig (cartesisch)
co?rdinatenstelsel xOy is gedefinieerd.
| Definitie Een punt in het cartesisch vlak is een passer en liniaal punt (penl-punt) als het punt het laatste punt is in een eindige rij P1, P2, ..., van punten, zodat elk punt tot de verzameling { (0,0), (1,0) } behoort, ?f kan worden verkregen
Een penl-lijn is een lijn die gaat door twee penl-punten. |
De volgende zes rijen zijn voorbeelden die aan de de voorwaarde P1, P2, ..., Pn-1, Pn voldoen:
Overigens is het soms in het geheel niet eenvoudig te bewijzen dat een dergelijke rij aan de voorwaarde van de penl-definitie voldoet.
| Stelling 1.1 Het snijpunt van twee penl-lijnen is een penl-punt. Een snijpunt van een penl-cirkel en een penl-lijn is een penl-punt. Een snijpunt van twee penl-cirkels is een penl-cirkel. |
Bewijs: Dat een rij Q1, Q2, ..., Qm van punten aan de voorwaarde van de
penl-definitie voldoet, betekent dat voor elke Qi moet gelden Qi = (0,0), of
Qi = (1,0) of Qi wordt verkregen op een van de manieren die in de definitie zijn
aangegeven met (i), (ii) en (iii).
(i)
Als Z het snijpunt is van twee penl-lijnen, dan zijn er penl-punten P,Q,R en S zodat Z is
het snijpunt van de lijnstukken PQ en RS.
(ii)
Als Z een snijpunt is van een penl-cirkel en een penl-lijn, dan zijn penl-punten P,Q,R en
S zodat Z is een snijpunt van het lijnstuk PQ en RS (de cirkel met middelpunt R
die gaat door S).
(iii)
Als Z een snijpunt is van twee penl-cirkels, dan zijn er penl-punten P,Q,R en S zodat Z is
een snijpunt van de cirkels PQ en RS.
In elk van de drie gevallen zijn er dus een rij P1,P2, ..., P, een rij Q1, Q2, ..., Q, een
rij R1, R2, ..., R en een rij S1, S2, ..., S die elk aan de penl-definitie voldoen.
De rij P1,P2, ..., P, Q1, Q2, ..., Q, R1, R2, ..., R , S1, S2, ..., S voldoet ook aan de
penl-definitie.
In elk van de drie gevallen voldoet dus ook de rij P1,P2, ..., P, Q1, Q2, ..., Q, R1, R2,
..., R , S1, S2, ..., S, Z aan de definitie.?
We zullen nu aantonen, dat de euclidische passer (dat.is een passer waarmee alleen een
enkele cirkel getekend kan worden die door een gegeven punt gaat uitgaande van een gegeven
middelpunt) equivalent is met de penl-passer (een passer waarmee we zoals gebruikelijk
cirkels kunnen tekenen).
Merk op, dat bij een euclidische passer de benen van de passer als het ware naar elkaar
toeklappen, als de de cirkel getekend is.
| Stelling 1.2a Zijn A, B en C drie penl-punten, dan is ABC (cirkel met middelpunt A en straal gelijk aan het lijnstuk BC) een penl-cirkel. |
| . |
|
Bewijs: (we volgen het bewijs zoals dat ook door Euclides in
zijn Elementen gegegeven is). A, B en C zijn drie gegeven penl-punten (zie figuur 1.1). Zij D een snijpunt van de cirkels AB en BA. D is dan een penl-punt volgens Stelling 1. Zij E het snijpunt van het gerichte lijn stuk DB en BC. E is nu een een penl-punt, omdat E het snijpunt is van de penl-cirkel BC en de penl-lijn DB. Zij F het snijpunt van het gerichte lijnstuk DA en de cirkel DE.. F is nu een penl-punt. Omdat BC=AF, is dus ABC = AF. AF is een penl-cirkel, dus ook ABC is een penl-cirkel.? |
|||
| We bekijken vervolgens alle punten (x,y) in het cartesisch vlak. We willen bepalen welke punten daarin penl-punten zijn. We beginnen met de punten (0,0) en (1,0). De x-as is dus een penl-lijn. Het punt (-1,) is een penl-punt, omdat het een snijpunt is van de x-as met de cirkel door (1,0) en met middelpunt (0,0). We kunnen dus op basis van dit soort overwegingen bewijzen dat de punten (n,0), dus alle roosterpunten op de x-as, penl-punten zijn. In deze punten kunnen we loodlijnen construeren. Daardoor komen we tot de volgende stelling (zie ook figuur 1.2). |
||||
|
|
|||
| Dat de x-as een penl-lijn is, wil nog niet zeggen, dat elk punt op de x-as
een penl-punt is. Hetzelfde geldt voor punten op een penl-cirkel. Zoals bekend is een rationaal getal een breuk m/n (met n?0), waarbij m en n gehele getallen zijn. Een re?el getal dat geen rationaal getal is heet irrationaal getal. We geven nu een definitie van het wiskundige begrip ring, waarbij we opmerken, dat dit een definitie is die alleen bedoeld is voor het gebruik bij de onderstaande meetkundige beschouwingen (in de algebra wordt een meer gegeneraliseerde definitie van ring gebruikt). |
||||
| Definitie Een deelverzameling van de re?le getallen is een ring F (Engels: field), indien geldt (i) 0 en 1 behoren tot F; (ii) voor iedere a, b in F geldt: a+b in F, a-b in F, ab in F; (iii) voor iedere a en b?0 in F geldt: a/b in F. Een ring F heet euclidisch, als voor iedere x>0 in F geldt: ?x in F. |
| . |
| Stelling 1.3 De penl-getallen vormen een lichaam. |
| . |
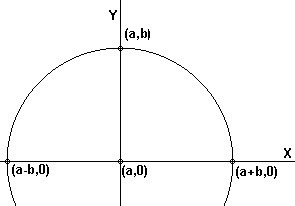
| figuur 1.3 | figuur 1.4 |
 |
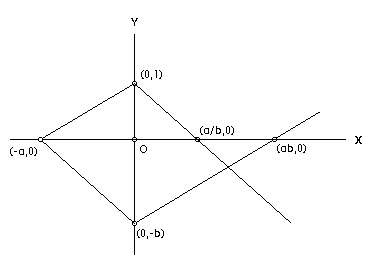 |
Bewijs: Het bewijs, dat gebaseerd is op euclidische constructies van hoeken, segmenten en evenwijdige lijnen, kunnen we afleiden uit figuur 1.3 en figuur 1.4. ?
| figuur 1.5 | 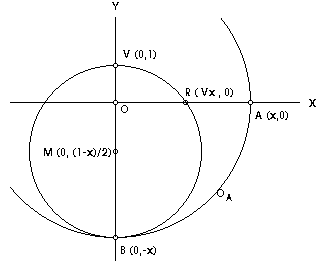 |
Uit de gegeven definitie volgt na beschouwing van figuur 1.5 heel gemakkelijk ook
| Stelling 1.4 De penl-getallen vormen een euclidische ring. |
De betekenis van "x is een kwadraat in de ring F" is, dat x
een element is van F en dat er een getal y in F bestaat zodat y2=x.
Met andere woorden: het getal x is een element van F desda ?x
is een element van F.
Dus een ring F is euclidisch desda elk positief getal van F een kwadraat is in F.
Gevolg
De ring Q (van de rationale getallen) is geen
euclidische ring. Immers, (bijvoorbeeld) 2 is zeker rationaal, maar ?2
is dat duidelijk niet.
We geven nu een algebraische constructie die van veel belang blijkt te zijn voor
verdere meetkundige beschouwingen.
We zullen een gegeven niet-euclidische ring uitbreiden een element of met meerdere
elementen, opdat de nieuwe verzameling die dan ontstaat, opnieuw een ring is.
Gaan we bijvoorbeeld uit van de ring F = Q en kiezen we d=5 (zie stelling 5), dan bekijken we de verzameling getallen p+q?5, waarbij p en q element zijn van Q. Dan zal blijken, dat die nieuwe verzameling een ring is.
| Stelling 1.5 Is F een ring en is d een positief getal in F, terwijl ?d geen element is van F, dan is de de verzameling V={p + q?d | p, q in F} een ring. |
Bewijs: Het is noodzakelijk aan te tonen, dat de som, het verschil, het
product en het quotient van de getallen p1+q1?d en p2+q2?d opnieuw van de vorm p3+q3?d is, waarbij pi en qi
elementen zijn van F.
Het bewijs daarvan verloopt voor de som en het verschil zeer elementair.
Voor het product geldt:
(p1+q1?d)(p2+q2?d) = (p1p2 +
q1q2d)+(p1q2+p2q1)?d.
Voor het quotient moeten we iets meer doen.
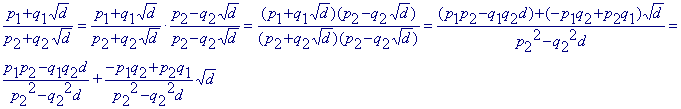
Uit beide laatste afleidingen blijkt, dat het product en het quotient van twee elementen
uit V eveneens elementen zijn van V.?
| Definitie Als F een ring is, dan noemen we de ring V={p+q?d | p, q in F}een kwadratische uitbreiding van F. We schrijven V = F[?d]. Zijn p en q rationaal, dan schrijven we de kwadratische uitbreiding van Q (de verzameling rationale getallen) met ?d dus als Q[?d]. |
Opmerking
Het is niet zo eenvoudig uit te maken of een element van F (of van Q)
een kwadraat is in F of niet.
Zo is bijvoorbeeld (35-15?5)/2 een kwadraat in Q omdat het gelijk is aan ((5-3?5)/2)2.
Echter 2 is geen kwadraat in Q[?2] omdat kan worden aangetoond, dat er geen rationale getallen a
en b zijn, zodanig dat (a+b?2)2 = 2.
Volgens stelling 1.5 kunnen we een nieuwe ring maken bestaande uit getallen x + y?2 met x en y uit Q[?5]. De getallen in deze ring zijn dus van de vorm (p1+q1?5)+(p2+q2?5)?2, met p en q uit Q.
We kunnen nu verdere uitbreidingen van een ring F vastleggen, zoals in de volgende definitie is aangegeven.
| Definitie Als, uitgaande van een ring F, F1 = F[?d1], F2 = F1[?d2], ..., Fn = Fn-1[?dn] dan noemen we Fn een herhaalde kwadratische uitbreiding van F en schrijven Fn = F[?d1, ?d2, ..., ?dn]. De vereniging van alle herhaalde kwadratische uitbreidingen van Q geven we aan met E. |
We kunnen ons nu afvragen welke gedaante de getallen hebben die tot E
behoren.
Gemakkelijk is in te zien, dat E bestaat uit
alle reele getallen die kunnen worden geschrven met gebruik making van haakjes, gehele
getallen, de tekens +, -, x
en ? (of het teken / ) en het teken ?.
Geldt voor alle getallen in een ring F, dat het penl-getallen zijn, dan zijn de getallen
in de kwadratische uitbreiding F[?d] eveneens
penl-getallen. Dit volgt uit stelling 1.4.
Herhaalde toepassing geeft dan:
Als x een element is van een herhaalde kwadratische uitbreiding, dan is x
een penl-getal.
We komen zo tot de
| Stelling 1.6 Als x een element is van E, dan is x een penl-getal. |
Ook het omgekeerde van deze stelling is juist. Een schets van het bewijs daarvan volgt
nu.
Uitgaande van een verzameling punten construeren we nieuwe punten met behulp van passer en
liniaal. Deze nieuwe punten kunnen ontstaan als snijpunt van lijnen en cirkels, waarbij we
vergelijkingen kunnen gebruiken om de co?rdinaten van die punten te vinden. Bij het
oplossen van de stelsela vergelijkingen behoeven we alleen gebruik te maken van de vier
rekenkundige bewerkingen en van vierkantswortels. Men mag dus verwachten, dat de
co?rdinaten van elk te construeren punt in een (herhaalde) kwadratische uitbreiding van
de rationale getallen liggen.
De details over het gebruik van vergelijkingen laten we hier achterwege. We merken alleen
op, dat indien vergelijkingen van lijnen en cirkels worden gebruikt, waarvan de
co?fficienten in een ring F liggen, bewezen kan worden, dat ook de co?rdinaten van de
snijpunten element zijn van F of van een kwadratische uitbreiding van F.
We zijn nu klaar om de hoofdstelling voor penl-constructies in een cartesich co?rdinatenstelsel te geven.
| Stelling 1.7 De co?rdinaten van een penl-punt in een cartesich assenstelsel zijn elementen van een herhaalde kwadratische uitbreiding van de ring Q der rationale getallen. |
Bewijs: Zij P een penl-punt. Uit de definitie van een penl-punt weten we dat P dan het laatste element moet zijn in de rij P1, P2, ..., Pn van punten, waarvan elk gelijk is aan (1,0) of (0,1) of kan worden verkregen
| (i) | als snijpunt van twee lijnen, waarvan elke lijn door twee punten gaat uit de rij P1, P2, ..., Pn-1 (zo'n punt heet een eerder punt); |
| (ii) | als snijpunt van een lijn door twee eerdere punten en een cirkel, gaande door een eerder punt en met een eerder punt als middelpunt; |
| (iii) | als snijpunt van twee cirkels, waarvan elk door een eerder punt gaat en waarvan elk een eerder punt als middelpunt heeft. |
We kunnen de co?rdinaten van P1 (die zijn gelijk aan (1,0) of aan (0,1)) associ?ren met de rationale getallen. Voorts zien we dat elk punt Pi (i > 1) kan worden geassocieerd met een ring Fi waarbij de coordinaten van Pi elementen zijn van Fi, en wel zo, dat Fi = Fi-1 of anders Fi is een kwadratische uitbreiding van Fi-1.
Dus is Fn een herhaalde kwadratische uitbreiding van Q, en dus zijn de coordinaten van P element van Fn.?
De stelling zegt dat als x een penl-getal is, x dan element moet zijn
van E. Merk op, dat E
een ring is, omdat de penl-getallen een ring vormen (stelling 1.4). Omdat een ring het
getal 1 moet bevatten en daardoor ook alle rationale getallen, en omdat een euclidische
ring gesloten moet zijn onder de worteltrekking (als x > 0 element
van de ring, dan ook ?x element van de ring), kunnen
we vaststellen, dat E de kleinste euclidische
ring is.
Omdat Q de kleinste ring is, is E de kleinste euclidische ring.
Gevolg
Punt P is een penl-punt desda de coordinaten van P zijn elementen van E.
Het getal x is een penl-getal desda x is een element van E.
We hebben nu enkele algebra?sche gereedschappen om bij het werken met penl-punten te
gebruiken:
Als een punt in het cartesisch vlak gegeven is, dan is dat punt penl-construeerbaar desda
de coordinaten van dat punt behoren tot een herhaalde kwadratische uitbreiding van Q.
2. Trisectie
![]()
Bij het bewijs van de onoplosbaarheid van de in paragraaf 1 genoemde
(eerste twee) problemen gebruiken we verder nog de volgende stellingen uit de algebra.
| Stelling 2.1 Als de vergelijking axn + bxn-1 +...+ gx + h = 0 geheeltallige co?ffici?nten heeft met een rationale oplossing p/q, waarbij p en q onderling ondeelbaar (relatief priem) zijn, dan is p deelbaar op h en q deelbaar op a. |
Bewijs: Substitueer p/q voor x in de vergelijking en vermenigvuldig het resultaat met qn. We krijgen nu:
apn + bpn-1q +...+ gpqn-1 + hqn = 0
Omdat p deelbaar is op de rechterkant van de vergelijking en p ook
deelbaar is op alle termen die links van de term hqn staan, moet p
ook deelbaar zijn op deze laatste term. Echter p heeft geen gemeenschappelijke
factor met q, dus moet p deelbaar zijn op h.
Op dezelfde manier tonen we aan, dat q deelbaar moet zijn op apn,
en dus op a. ?
| Stelling 2.2 Als een derdegraads vergelijking met rationale co?ffici?nten geen rationale oplossingen heeft, dan is geen van de oplossingen een penl-getal. |
Bewijs: We gaan uit van de derdegraads vergelijking x3 +
ax2 + bx + c = 0, waarin a, b
en c ratoinaal zijn.
We nemen voorts aan, dat deze vergelijking een oplossing r heeft die wel
een penl-getal is.
Zij nu F0 = Q. Dan is er
een kleinste positief getal k zodat de vergelijking een penl-wortel heeft in de
herhaalde kwadrarische uitbreiding van Fk van de verzameling Q
van de rationale getallen met Fk = Q[?d1, ?d2, ..., ?dk].
Zij nu Fi = Q[?d1, ?d2, ..., ?di] voor i = 1,2, ..., k-1. Dus Fi
is een kwadratische uitbreiding van Fi-1 voor i = 1,2, ..., k.
Dit wil zeggen: Fi = Fi-1(?di).
Door onze veronderstelling met betrekking tot de oplossing die wel een penl-getal is,
bestaan er getallen p en q in Fi-1 zodat r = p + q?dk. Hierbij moet gelden q?0,
omdat anders r een element is van Fi-1, en dan is k
niet minimaal.
Uit de algebra?sche identiteit
(p ? q?dk)3 + a(p ? q?dk)2 + b(p ? q?dk) + c =
(p3 + 3pq2dk + ap2 + aq2dk + bp + c) ? (3p2+q3dk+2apq+bq)?dk
zien we dat p - q?dk eveneens een
oplossing is van de vergelijking.
De oplossingen p + q?dk en
p - q?dk verschillen, omdat q?0.
Zij t nu de derde oplossing van de vergelijking. Nu geldt dus
x3 + ax2 + bx + c = (x - t)(
x - (p+q?dk) )( x - (p-q?dk) = (x - t) (x2 - 2px + p2 - q2dk)
voor iedere x.
Vergelijken we de co?ffici?nten van x2 aan beide kanten, dan moet gelden a =
- t - 2p, waarbij dus t element is van Fi-1.
Echter, dit is in strijd met het feit met de minimaliteit van de waarde van k,
omdat t een wortel blijkt te zijn van de vergelijking waarbij t element is van Fi-1.
De veronderstelling is dus onjuist. ?
| Stelling 2.3 Er zijn drie penl-punten P, Q en R zodat ?PQR = t DESDA cos t is een penl-getal. |
| . |
| figuur 2.1 | 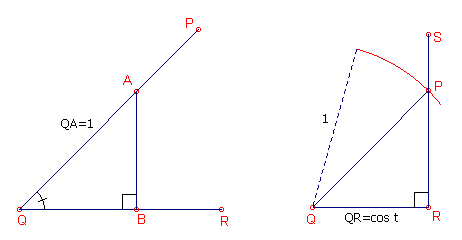 |
Bewijs: (zie figuur 2.1) Vooraf twee opmerkingen. (i) Met de te gebruiken
passer kunnen we afstanden "overzetten". (ii) Het is voldoende alleen scherpe
hoeken te beschouwen. In de linker figuur is de hoek PQR gegeven met grootte t. We kunnen nu het punt A op QP construeren zodat QA=1. Dan construeren we de loodlijn AB uit A op QP. Nu is cos t = QR. cos t is dus een penl-getal. Omgekeerd. Zij QR gegeven met QR=cos t.We kunnen nu het punt S construeren zodat RS^QR. De eenheidscirkel met middelpunt Q snijdt nu RS in het punt P. Nu is ?PQR = t.? |
We gebruiken verder nog een tweetal trigoniometrische formules:
sin(A+B) = sinAcosB+cosAsinB
cos(A+B) = cosAcosB-sinAsinBUit deze formules leiden we heel gemakkelijk af
sin2A = 2sinAcosA
cos2A = cos2A-sin2A = 1 - 2sin2A=2cos2A - 1
sin3A = sin(A+2A) = sinA.(4cos2A - 1)
cos3A = cos(A+2A) = 4cos3A-3cosA
Vermenigvuldigen we .deze laatste identiteit met 2 en ordenen we de termen, dan krijgen we de identiteit
(2cosA)3 - 3.(2cosA) - 2 cos3A = 0
Omdat cos(3(A+120?)) = cos(3(A+240?)) = cos3A, kunnen we eenvoudig de juistheid van de volgende stelling verifi?ren.
| Stelling 2.4 De getallen 2cosA, 2cos(A+120?) en 2cos(A+240?) zijn oplossingen van de vergelijking x3 - 3x - 2cos(3A) = 0. |
Nu is cos 60?=1/2. Kiezen we vervolgens 3A=60, dan zien we volgens stelling 2.4
dat de vergelijking x3 - 3x - 1 = 0 de oplossingen
2cos 20?, 2cos 140? en 2cos 260? heeft.
De vergelijking x3 - 3x - 1 = 0 heeft gehele co?ffici?nten,
maar heeft geen rationale oplossingen (volgens stelling 2.1).
Volgens stelling 2.2 is dus geen van de oplossingen van de vergelijking een penl-getal.
We hebben nu de volgende belangrijke stelling bewezen.
| Stelling 2.5 Het getal cos 20? is geen penl-getal. |
Gevolg
Een het belangrijke gevolg van stellng 2.5 is dan weer, dat een hoek 60? niet kan worden
verdeeld in drie gelijke stukken met penl. We hebben dus een hoek (die zelf wel
gemakkelijk kan worden geconstrueerd) gevonden, waarvan trisectie niet mogelijk is.
Door het vinden van deze hoek kunnen we dus vaststellen, dat het probleem van de trisectie
van de hoek (met penl) onoplosbaar is.
3.
Verdubbeling van de kubus en kwadratuur van de cirkel ![]()
We bewijzen allereerst de
| Stelling 3.1 Het getal 3?2 is geen penl-getal. |
Bewijs: We bekijken de vergelijking x3 - 2 = 0. Volgens stelling 2.1 heeft deze vergelijkin geen rationale oplossing. En volgens stellling is het getal 3?2 dat wel een oplossing van de vergelijking is, dus geen penl-getal.?
Gevolg
Het probleem van de verdubbeling van de kubus is met penl onoplosbaar.
De oude Grieken hadden zelf wel enig idee omtrent de onoplosbaarheid van de drie
genoemde problemen.
Het eerste echte bewijs van de onoplosbaarheid van de eerste twee problemen werd
gegeven door de weing bekende Franse wiskundige Pierre Laurent Wantzel (1814-1848). Het bewijs werd
door Wantzel op 23-jarige leeftijd -hij was nog student- gepubliceerd
Het derde klassieke constructieprobleem, de kwadratuur van de cirkel, is eveneens onoplosbaar. Om dit aan te tonen is het noodzakelijk en voldoende te bewijzen, dat het getal p geen penl-getal is.We kunnen bewijzen (maar doen dat niet hier) dat
| Stelling 3.2 Elk penl-getal is oplossing van een polynoom-vergelijking met gehele co?ffici?nten. |
Oplossingen van een polynoom-vergelijking met gehele co?ffici?nten worden algebra?sche
getallen genoemd. De penl-getallen vormen een deelverzameling van de algebra?sche
getallen. Re?le getallen die geen oplossingen zijn van een polynoom-vergelijking met
gehele co?ffici?nten, worden transcendente getallen genoemd.
In 1882 toonde de Duitse wiskundige Ferdinard von Lindemann (1852-1939) aan, dat het getal
p een transcendent getal is. Daarmee toonde hij dus tevens aan
dat het laatste van de drie klassieke meetkunde-problemen, de kwadratuur van de cirkel,
eveneens onoplosbaar is.
Niet-penl oplossingen. Zie de pagina "Cisso?de van Diokles" voor een niet-penl oplossing van het kubusverdubbelingsprobleem.
? Zie de pagina "Maantjes van Hippocrates" voor kromlijnige figuren die wel kwadreerbaar zijn.
4. Enkele
conclusies ![]()
In stelling 2.5 hebben we bewezen, dat het niet mogelijk is een hoek van 20? te
construeren met penl.
Hieruit volgt onmiddellijk, dat het een penl-constructie van een regelmatige 18-hoek
evenmin bestaat. En dus ook niet van een regelmatige 9-hoek.
Hierboven (in paragraaf 2) hebben we enkele goniometrische formules afgeleid. Daarmee gaan we nog heel even door.
sin
4A = sin 2*(2A) = 2sin2Acos2A = 4sin(A)(2cos?A - 3cosA)
cos 4A = cos 2*(2A) = 2cos?2A - 1 = 8cos4A - 4cos2A
+ 1
cos 7A = cos(3A + 4A) = 64cos7A - 112cos5A + 56cos3A - 7cosA.
Na vermenigvuldiging van beide leden van de laatste identiteit met 2 en ordening van de termen krijgen we:
(2cosA)7 - 7(2cosA)5 + 14(2cosA)3 - 7(2cosA) - 2 cos(7A) = 0
Stellen we nu 7A = 360?, dan is eenvoudig in te zien, dat de vergelijking
x7 - 7x5 + 14x3 -7x - 2 = 0
zeven wortels heeft, te weten xk = 2cos(360k/7) voor k
= 0, 1, ...,6.
Deze wortels zijn echter niet alle verschillend, immers x1=x6, x2=x5
en x3=x4, terwijl x0 = 2.
Uit dit laatste volgt een ontbinding van het linkerlid van de vergelijking. Dit geeft dan
(x3 + x2 - 2x - 1)(x - 2) = 0
Hieruit volgt de
| Stelling 4.1 De vergelijking x3 + x2 - 2x - 1 = 0 heeft de oplossingen 2cos(360/7), 2cos(360*2/7) en 2cos(360*3/7). |
En hieruit volgt onmiddellijk, volgens stelling 2.2, de
| Stelling 4.2 Een penl-constructie van een regelmatige 7-hoek is niet mogelijk. |
Nu rijst natuurlijk de vraag "Welke regelmatige n-hoeken zijn dan wel met
penl te construeren?".
Deze vraag is deels precies te beantwoorden en deels ook niet. We zullen hiertoe
bijzondere priemgetallen gebruiken.
5. Polygonen
en priemgetallen van Fermat
We bekijken getallen van de vorm 2m + 1. Deze getallen, met een
bijzondere waarde van m, noemen we getallen van Fermat of Fermat-getallen
(naar de Franse wiskundige Pierre de Fermat, 1601-1665).
We hebben de volgende algebraische identiteit
x2r+1 + 1 = (x + 1)(x2r
- x2r-1 + x2r-2 - x2r-3 + x2r-4
+ ... - x3 + x2 - x + 1)
We stellen nu x = 2q. De identiteit gaat dan over in
2q(2r+1) + 1= (2q + 1)( ... )
Daaruit blijkt dat 2q(2r+1) deelbaar is door 2q+1.
Dus als we ervan uitgaan, dat 2m+1 geen triviale factoren heeft, dan kan m
geen oneven factor hebben groter dan 1. Dus moet m een macht zijn van 2. We
stellen nu m = 2n en spreken af dat we schrijven
Fn = 22n + 1
De getallen Fn, met n = 0, 1, 2, ... zijn nu de hierboven bedoelde Fermat-getallen.
Fermat was er omstreeks 1640 van overtuigd, dat alle Fermat-getallen priem waren. In 1659
beweerde hij zelfs daarvoor een bewijs te hebben gevonden (hij beweerde overigens wel
meer).
In 1732 echter vond Leonard
Euler (1701-1783) dat F5 = 225 + 1 geen
priemgetal was. En inderdaad:
F5 = 4294967297 = (641) * (6700417)
Overigens is het op dit moment zo, dat er geen enkel Fermat-getal met n > 4
bekend is dat wel een priemgetal is.
In 1992 bleek bijvoorbeeld dat F22, dat meer dan een miljoen cijfers telt,
samengesteld is. Voorts is ook bekend, dat F23471 geen priemgetal is.
Vandaag de dag zijn er slechts vijf bekende Fermat-priemgetallen:
| n | 0 | 1 | 2 | 3 | 4 |
| Fn | 3 | 5 | 17 | 257 | 65537 |
Carl Friedrich Gauss (1777-1855) gaf als eerste een penl-constructie van de regelmatige 17-hoek. De reeds eerder genoemde Laurent Wantzel was de eerste die bewees, dat, als een regelmatige n-hoek, met n priem, penl-construeerbaar is, n dan een Fermat-priemgetal moet zijn.
We kunnen dus (iets uitgebreider, echter niet hier) bewijzen:
| Stelling 5.1 (Stelling van Gauss-Wantzel) Een regelmatige n-hoek is penl-construeerbaar desda n is een geheel getal groter dan 2 zodat de grootste oneven factor van n gelijk is aan 1 of gelijk is aan een product van verschillende Fermat-priemgetallen. |
6. De trisectie
van de hoek anders bekeken ![]()
De oude Grieken hebben bij het zoeken naar een penl-constructie voor de trisectie van de
hoek verschillende niet-penl-methoden gevonden.
6.1. Archimedes ![]()
We geven hier als eerste een methode van trisectie die wordt toegeschreven aan Archimedes (287-211 vC), vermoedelijk gevonden omstreeks
225 vC. Deze methode gaat als volgt (zie figuur 6.1).
| figuur 6.1 | 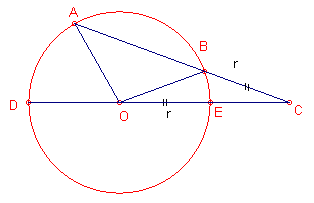 |
Teken een koorde AB van een cirkel met straal r, zodat het verlengde daarvan,
BC, gelijk is aan r. Verbind C met het middelpunt O van de cirkel en bepaal de
snijpunten D en E van CO met de cirkel. Nu is bg(AD) = 3 . bg(BE). Dus, hoek
AOD = 3 . hoek EOB. Duidelijk is, dat deze methode niet daadwerkelijk de gewenste trisectie oplevert. De methode van Archimedes bracht echter de Franse wiskundige Francois Viete (Vieta, 1540-1603) op een methode (ongeveer in 1590) die dat wel doet. |
Bij diens methode wordt ook gebruik gemaakt van een passer en een
zogenoemde gemerkte liniaal (dat is een liniaal waarop merktekens kunnen worden
gezet). Van zo'n gemerkte liniaal is ook gebruik gemaakt bij de methode van
Archimedes..Viete gebruikte een gemerkte liniaal waarop twee merktekens C en D zijn
geplaatst, zodat CD=1 (de gemerkte liniaal is dus de lijn CDB)..
Uitgaande van de scherpe hoek OAB tekenen we nu de cirkel met middelpunt A en straal
gelijk aan 1 (zie figuur 6.2).
| figuur 6.2 | 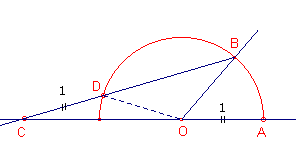 |
De gedachte achter de constructie is de liniaal die door B gaat, zo te schuiven, dat D
op de cirkel en C op de lijn AO komt te liggen. Zij nu hoek OCD = x. Nu is de
buitenhoek ODB van gelijkbenige driehoek OCD gelijk aan 2x. Ook driehoek ODB is
gelijkbenig, zodat hoek DOB eveneens gelijk is aan 2x. De buitenhoek AOB van
driehoek OCB is dus gelijk aan De trisectie kan dan gevonden worden door een lijn door O evenwijdig aan CB te tekenen. |
| |
|
 |
Klik hier > De hiernaast afgebeelde trisector wordt wel trisector van Pascal genoemd. Referentie: |
In een iets andere constructie, maar wel gebaseerd op de methode
van Vieta, wordt eveneens gebruik gemaakt van een cirkel en de zogenoemde neusis
(dat is een gemerkte liniaal).
Klik hier >![]() <
voor een CabriJavapplet van de deze constructie.
<
voor een CabriJavapplet van de deze constructie.
6.2. Nicomedes' conchoide ![]()
De meest bekende van de Griekse pogingen is wellicht die van Nicomedes (ca. 180 vC). Hij gebruikte een kromme lijn die bekend
staat als conchoide.
| figuur 6.3 | 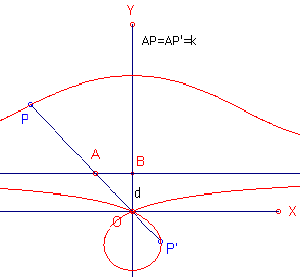 |
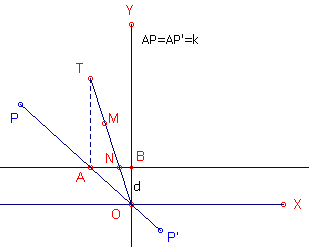 |
Uitgaande van een cartesischcoordinaten stelsel xOy nemen
we een lijn AB parallel aan de x-as en op een afstand d daarvan. Op de
lijn OA kiezen we twee punten P en P' zodat AP = AP' = k
(waarbij k een constante is). Bij verplaatsing van het punt A over de lijn AB
doorlopen de punten P en P' de conchoide (zie figuur 6.3, links).
De vergelijking van de kromme is in dit geval (x2 + y2)(x - d) - k2x2 = 0.
Afhankelijk van de waarde van k heeft de kromme een knooppunt (k > d),
een buigpunt (k = d) of een singulier punt (k < d).
De conchoide kan nu gebruikt worden voor de trisectie van de hoek YOA (zie figuur 6.3,
rechts).
Bepaal het voetpunt B van de loodlijn uit A op OY. Beschrijf vervolgens een conchoide
waarbij k gelijk wordt genomen aan 2AO. Bepaal vervolgens het snijpunt T van de loodlijn
in A op AB met de kromme. De lijn OT snijdt de lijn AB in N. Het punt M is het midden van
NT.
Nu is: MT=MN=MA (Stelling van Thales).
Maar NT = 2OA (vanwege de constructie van de conchoide).
Dus is MA=OA.
Nu geldt dus hoek AOM = hoek AMO = 2 . hoek ATM = 2 . hoek TOY.
Zodat hoek AOM = 2/3 . hoek YOA, en dus hoek TOY = 1/3 . YOA.
Klik hier >![]() <
voor een CabriJavapplet ter illustratie van de concho?de van
Nicomedes.
<
voor een CabriJavapplet ter illustratie van de concho?de van
Nicomedes.
Zie verder ook de pagina "Algemene cisso?den".
6.3. Apollonius ![]()
De bekendste methode voor de trisectie van de hoek wordt toegeschreven aan Apollonius van Perga (265-190 vC). Bij deze methode wordt
eveneens gebruik gemaakt van een gemerkte liniaal.
| figuur 6.4 | 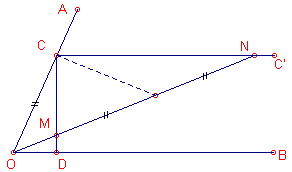 |
(Zie figuur 6.4). Zij AOB de gegeven hoek. We kiezen een willkeurig punt C op OA en
tekenen de aan OB evenwijdige lijn CC' door C. D is het voetpunt van de loodlijn uit C op
OB. We kiezen vervolgens de afstand MN = 2OC die met behulp van twee merktekens M en N op de liniaal wordt overgrbracht. We plaatsen nu de liniaal zo, dat de punten O,M en N collineair zijn, waarbij M op CD en N op CC' liggen. De lijn OM is dan een trisectrice van hoek AOB. |
Klik hier >![]() <
voor een CabriJavapplet van bovenstaande constructie.
<
voor een CabriJavapplet van bovenstaande constructie.
6.4. Hippias' kwadratrix ![]()
De Griekse meetkundige Hippias van Elis (ca. 425 vC) ontdekte een kromme die eveneens
gebruikt kan worden bij het trisectie-probleem.
In figuur 6.5 is X een willekeurig punt op boog AC. De lijn MN is evenwijdig aan OA. Als
de straal OX eenparig draait, vanuit de positie OC naar de positie OA en het lijnstuk MN
eenparig beweegt vanuit de positie CB naar de positie OA, dan beschrijft het punt P, het
snijpunt van OX en MN, een kromme lijn die kwadratrix wordt genoemd.
| figuur 6.5 | 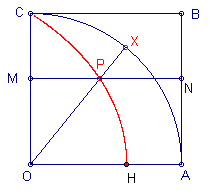 |
Duidelijk is, dat indien OX 1/n-de deel van de afstand van C naar A heeft
afgelegd, dit ook het geval is voor MN. Maken we daarom CM = 1/3 CO, dan verdeelt de lijn OX de rechte hoek in drie gelijke delen. Verdelen we nu OM in drie gelijke stukken, dan kunnen we een punt P' op de kromme vinden, zodat OP' een trisectrice is van hoek AOX (zie hiervoor de CabriJavapplet). Dit gaat natuurlijk ook op voor elke andere hoek. Deze methode is dus niet alleen te gebruiken bij de trisectie van een hoek, maar ook bij zogenoemde multisectie. Het probleem van de trisectie wordt door het gebruik van de kwadratrix dus als het ware "vertaald" naar het eenvoudig op te lossen probleem van het verdelen van een lijnstuk in gelijke stukken. |
De naam van de kromme is afgeleid van het gebruik ervan bij een ander (reeds eerder genoemd) klassiek onoplosbaar penl-probleem, namelijk de kwadraatuur van de cirkel (vandaar de naam "kwadratrix").
Klik hier >![]() <
voor een CabriJavapplet ter illustratie van de trisectie met behulp van
de kwadratrix.
<
voor een CabriJavapplet ter illustratie van de trisectie met behulp van
de kwadratrix.
Geven we het snijpunt van de kwadratrix en het lijnstuk OA met H, dan kunnen we ons
afvragen wat de lengte is van het lijnstuk OH.
Het is ook de Grieken niet ontgaan, dat de dynamische definitie van de kromme niet opgaat
voor het punt H. Immers het punt H is geen snijpunt van een lijn OX met een lijn MN. We
kunnen dus hoogstens spreken van de " limietwaarde van OH " als X
nadert tot A en tegelijkertijd ook M nadert tot O.
We zullen hier deze limietwaarde op "moderne" wijze afleiden.
Kiezen we OA en OC als assen van een cartesisch stelsel waarbij
OA = OC = 1. Stellen we nu de coordinaten van P gelijk aan (x,y)
en hoek XOA = j. Dan is tan(j) = y/x,
zodat y = x.tan(j).
De grootte van j is echter ook uit te drukken in x en y.
We hebben namelijk
y : bg(HP) = 1 : bg(AX) of y :
j = 1 : 2p/4.
Zodat j = y . p/2.
De vergelijking van de kwadratrix is dus (impliciet) gegeven
door y = x . tan(y*p/2).
Hieruit volgt voor de x-coordinaat van een willekeurig punt (dus ook H) van de
kromme: x = y / tan(y . p/2).
Nu is
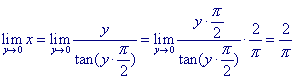
Bij gegeven O en H, waarbij OH = 2 / p kunnen we nu gemakkelijk
(met behulp van wat rechthoekige driehoeken; zie ook figuur 6.6) een lijnstuk construeren
met lengte ?p. En daarmee is het probleem van de kwadratuur
van de cirkel met gebruikmaking van de kwadratrix opgelost: we kunnen een vierkant
construeren, waarvan de oppervlakte gelijk is aan p.
Als illustratie is in onderstaande figuur (zie figuur 6.6) een vierkant ORST
geconstrueerd (niet met penl alleen ), waarvan de oppervlakte gelijk aan p / 2.
De lezer ga na, dat OK = p/2 (via de rechthoekige
driehoek HCK), en dat OR = ?(p/2)
(via de niet getekende rechthoekige driehoek ARK).
Bij gevolg is de oppervlakte van het vierkant beschreven op OR gelijk aan p/2.
| figuur 6.6 | 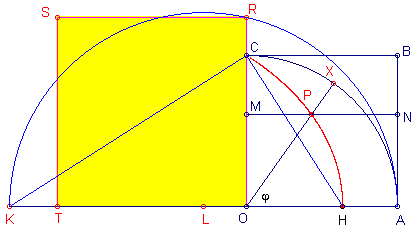 |
Zie ook de pagina "Algemene cisso?den", waarop de Trisectrix van Maclaurin (hoektrisectie) wordt behandeld.
Zie ook de pagina "Cisso?de van Diokles" voor een tweetal oplossingen van de verdubbeling van de kubus (Delisch probleem).
Zie eventueel ook: Een misvatting... (artikel, PDF-bestand, ca. 60Kb).
7. Download
De figuren die op deze pagina gebruikt zijn in de CabriJavapplets kunnen in ?en bestand
via deze website worden gedownload.
Klik hier om het downloaden te
starten (ZIP-bestand, ca. 7kB)
![]()
De figuren op deze pagina zijn getekend met behulp van The
Geometer's Sketchpad en met Cabri Geometry II.
[trisect.htm] laatste wijziging op: 24-06-08