Cabri: Euclidische passer en moderne passer
Overzicht ][ Cabri-FAQ(41) | Elementen | Passermeetkunde
Zie de pagina CabriFAQ(41): "Kent Cabri het begrip 'Euclidische passer'?
1. De passers
![]()
Euclides schrijft in zijn Elementen in Postulaat 3:
| En [laat ge�ist zijn] dat met elk middelpunt en elke afstand (bedoeld is de straal vastgelegd als een lijnstuk; dk) een cirkel beschreven wordt. |
En dat moet dan worden uitgelegd als:
een cirkel kan getekend worden met een gegeven middelpunt gaande door een
gegeven punt.
De oud-Griekse opvatting was dan, dat na het tekenen van de cirkel de benen van de passer
weer inklappen.
Men spreekt in dit geval van een Euclidische passer (Eng. collapsible
compasses).
Op de pagina "Passermeetkunde" hebben we reeds laten zien, dat constructies met de Euclidische passer en de moderne passer - de benen klappen bij dit type niet in - equivalent zijn.
We laten dat hieronder nogeens zien, maar dan via Cabri-constructies
met gebruikmaking van Cabri-macro's.
We zullen dus een cirkel construeren met een gegeven lijnstuk als straal en een gegeven
punt als middelpunt, waarbij we uitsluitend gebruik maken van de Euclidische passer en
zonodig een (Euclidische) liniaal.
2. Basisconstructies
![]()
We geven hieronder enkele basisconstructies met behulp van de Euclidische passer (E-passer);
de bewijzen van de constructies laten we achterwege.
Daarna zullen we de equivalentie laten zien tussen de Euclidische
passer en de moderne passer.
Maar eerst defini�ren we een Cabri-macro voor de Euclidische passer.
Definitiestappen:
We gaan ervan uit, dat A het middelpunt is van de cirkel die door B gaat. De punten A en B
zijn in ligging gegeven.
1. Cirkel(A, B)
2. Beginobjecten(A, B) - de volgorde van de punten is hier belangrijk.
3. Eindobjecten(1) - gebruik dan de bestandsnaam 'E-Passer'.
Hiermee is de macro:E-passer vastgelegd. �
| Constructie 1
De middelloodlijn van een lijnstuk |
Beschrijving:
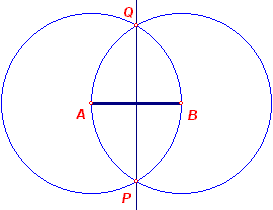 |
A en B zijn de eindpunten van het lijnstuk. Deze punten zijn dus in
ligging gegeven.Het lijnstuk zelf is voor de constructie niet noodzakelijk. 1. E-Passer(A, B) 2. E-Passer(B, A) 3. Snijpunten(1, 2) - dit zijn de punten P en Q. 4. Lijn(P, Q) � |
| Constructie 2
De loodlijn in/uit een punt op een lijn of lijnstuk |
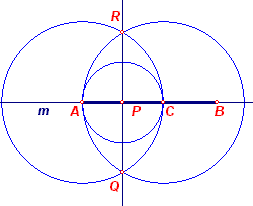 |
De lijn of het lijnstuk wordt bepaald door de in ligging gegeven punten A
en B. Het punt P waardoor de loodlijn op AB gconstrueerd moet worden, is eveneens in
ligging gegeven. Nb. P ligt niet recht boven A. 1. Lijn(A, B) = m 2. E-Passer(P,A) - dit geeft C als tweede snijpunt met m (de lijn van 1). 3. E-Passer(A, C) 4. E-Passer(C, A) 5. Snijpunten(3, 4) - dit zijn de punten Q en R. 6. Lijn(Q, R) - deze lijn gaat gaat door P. |
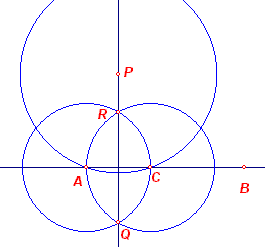 |
In de situatie hierboven ligt het punt P op
AB. Als P buiten AB ligt verloopt de constructie analoog. � |
| x |
| Constructie 3
De loodlijn in een eindpunt van een lijnstuk op dat lijnstuk |
Beschrijving:
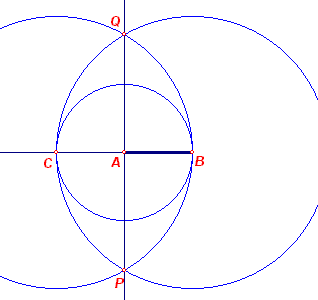 |
Het lijnstuk is bepaald door de in ligging gegeven punten A en B. We
zullen de loodlijn in A op AB construeren. Het lijnstuk zelf is voor de constructie niet
noodzakelijk. 1. HalveLijn(A, B) - hierbij kan ook Lijn(A, B) worden gebruikt. 2. E-Passer(A, B) - deze cirkel heeft met AB een tweede snijpunt C. 3. E-Passer(C, B) 4. E-Passer(B, C) 5. Snijpunten(3, 4) - dit zijn de punten P en Q. 6. Lijn(P, Q) - deze lijn gaat door het punt A. � Op
basis van Constructie 3 leggen we een macro vast die we gebruiken in Constructie 4. |
| x |
| Constructie
4 Rechthoek met gegeven zijden |
Klik hier >![]() < voor een CabriJavapplet
bij deze constructie.
< voor een CabriJavapplet
bij deze constructie.
Beschrijving:
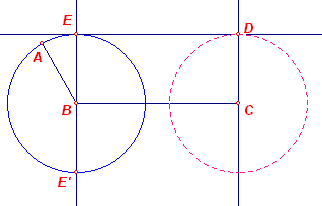 |
De lengtes van de zijden zijn AB en BC, waarbij AB niet loodrecht staat
op BC. We gaan uit van de in ligging gegeven punten A, B, C. We construeren de rechthoek BCDE, met BE = CD = AB. 1. E-Loodlijn(EindpuntLijnstuk)(B, C) - de volgorde B, C is belangrijk. 2. E-Loodlijn(EindpuntLijnstuk)(C, B) 3. E-Passer(B, A) 4. Snijpunten(3, 1) - de snijpunten zijn E em E'. Kies een van deze punten, bijvoorbeeld E. 5. E-Loodlijn(EindpuntLijnstuk)(E, B) 6. Snijpunt(5, 2) - dit geeft het punt D En hiermee is de gewenste rechthoek BCDE gevonden. � |
Opmerking
Het is nu mogelijk een cirkel te construeren met middelpunt C waarvan de straal gelijk is
aan AB (zie de gestippelde cirkel in de figuur hierboven).
We zullen in de volgende paragraaf, Equivalentie, laten zien, dat we
daarvoor niet specifiek een rechthoek nodig hebben.
Maar in principe is hiermee reeds het bewijs van de equivalentie van de constructies met
een Euclidische passer en een moderne passer gegeven.
De volgende constructie maakt echter alleen gebruik van een Euclidische
passer!
[einde Opmerking]
| Stelling 1 De constructie van een cirkel met een gegeven punt als middelpunt en een gegeven lijnstuk als straal is mogelijk met gebruikmaking van een Euclidische passer (E-passer). |
Klik hier >![]() < voor een CabriJavapplet
bij deze stelling.
< voor een CabriJavapplet
bij deze stelling.
Bewijs:
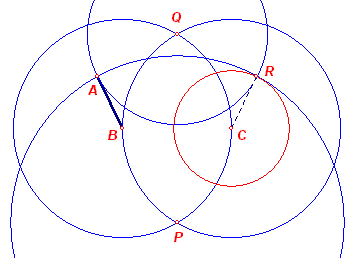 |
We geven hieronder een bewijs door middel van constructie. We gaan uit
van een lijnstuk AB als straal en een punt C als middelpunt (de punten A, B, C zijn in
ligging gegeven). Beschrijving: 1. E-Passer(B, C) 2. E-Passer(C, B) 3. Snijpunten(1, 2) - dit zijn de punten P en Q. 4. E-Passer(P, A) 5. E-Passer(Q, A) 6. Snijpunten(4, 5) - dit zijn de punten A en R. 7. E-Passer(C, R) Deze laatste cirkel is dan de gevraagde cirkel. Waarmee het gestelde is aangetoond. � |
Opmerking
Uiteraard kan op Stelling 1 weer een Cabri-macro (macro:E-CirkelMR)
worden gebaseerd waarmee de cirkel (C, AB) kan worden getekend.
Er zij ook opgemerkt dat de Cabri-functie Passer deze mogelijkheid
eveneens biedt (zie de definitie van de macro:E-Passer).
[einde Opmerking]
Download
![]()
De hierboven genoemde macro's (geschikt voor Cabri II en Cabri II
Plus) kunnen samen met de figuren die gebruikt zijn bij de CabriJavapplets, worden
gedownload via deze website.
Klik hier om het downloadproces te starten
(ZIP-bestand, ca. 10 kB).
| [1] | NICHOLAS D. KAZARINOFF: Ruler and the round, Dover Publications (Mineola, USA, reprint 2003) |
| [2] | GEORGE E. MARTIN: Geometric Constructions, Springer (New York, 1998) |