Benaderingsconstructies van Mascheroni
Overzicht ][ Passermeetkunde | Inversie | Elementen | Meetkunde
Deze pagina is een vervolg op de pagina "Passermeetkunde".
Zie eventueel ook de pagina "Trisectie van een hoek".
1. Hulpconstructie
![]()
In de paragrafen 2 en 3 wordt gebruik gemaakt van onderstaande, ook door Mascheroni gebruikte, hulpconstructie.
Deze constructie is gedeeltelijk terug te vinden in Voorbeeld
2 (op de pagina Passermeetkunde).
| figuur 1 | 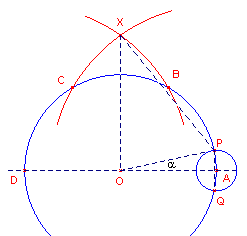 |
Zij OA = r. De punten B, C, D worden op de gebruikelijke manier geconstrueerd. Het punt X wordt bepaald door de cirkels A(AC) en D(DB). Het punt P is een willekeurig punt op de cirkel, waarbij hoek POA = a. Nu is: AC = BD = �(4r2 - r2) = r�3. en OX = �(3r2 - r2) = r�2. Met de cirkel A(AP), die de grote cirkel ook in Q snijdt, kan het verband worden gevonden tussen a, de straal r en lengte van PQ: PQ = 2r sin a |
We hebben nu in driehoek OPX (cosinusregel):
PX2 = PO2 + XO2
- 2 .PO .XO .
cos POX, dus
PX2 = r2 +
2r2 - 2 . r . r�2 . sin a
Dus (formule van Mascheroni; zie ook de pagina "G�om�trie
du compas"):
![]()
Door een geschikte keuze van construeerbare waarden van a slaagt Mascheroni er in om met de fomule voor PX benaderingsconstructies af te leiden voor (om.) de verdubbeling van de kubus en de rectificatie van de cirkel.
2. Verdubbeling van de kubus
![]()
Kies a = 30�.
We stellen nu r = 1.
We hebben dan PX = �(3-�2) = 1,2592801.
Voor de ribbe x van de kubus waarvan de inhoud gelijk is aan 2, hebben we x3
= 2.
Dus:
x = 1,2599211
De fout in de benadering is dus x - PX = 0,0006409.
Als de straal van de cirkel gelijk is aan 1 m, dan is de fout dus iets meer dan 0,6 mm.
Voor de constructie van x (in casu het punt P) geeft Mascheroni het volgende.
| figuur 2 | 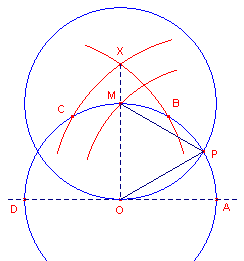 |
De punten B, C, D en X worden geconstrueerd volgens de hulpconstructie. Cirkel A(OX) geeft het punt M. Cirkel M(MO) geeft het punt P. We dienen nu aan te tonen, dat hoek POA = 30�. Driehoek OPM is gelijkzijdig. bg AP = 90� - bg PM = 90� - 60� = 30�. � |
3. Benadering van p (pi), rectificatie van de cirkel
![]()
Kies a = 60�.
Ook nu stellen we r = 1.
In dit geval geldt, dat P met het punt B samenvalt.
Volgens de formule van Mascheroni is dan BX = �(3 - �6).
| figuur 3 | 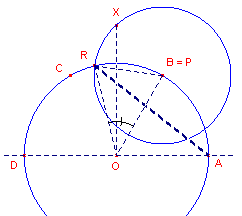 |
Het punt R op de cirkel wordt bepaald door B(BX); zodat BX = BR. Het lijnstuk AR is nu een benadering van �p (een kwart van de omtrek). Zij hoek BOR = j. In driehoek BOR (gelijkbenig) is dan: BR = 2 sin j/2, zodat j/2 = arcsin BR/2. Voor AR in driehoek OAR hebben we dan: AR =2 sin (AOR/2) = 2 sin(30� + arcsin BR/2). Een benadering van de omtrek van de halve cirkel, waarde p, is dus: 2 AR = 4 sin(30� + arcsin ��(3 - �6)) = 3,14239917. |
De fout in de benadering is dan 0,0008065.
Bij een straal van 1 m, is de fout dus iets meer dan 0,8 mm.
Klik hier ![]() voor een CabriJavapplet
van deze constructie.
voor een CabriJavapplet
van deze constructie.
Opmerking
Zie ook de pagina "Benaderingen van p".
4. Kwadratuur van de cirkel
![]()
Door de benadering van p in paragraaf 3 is
eigenlijk ook dit klassieke probleem opgelost.
Immers zij x de ribbe van het vierkant, dan dienen we x zo te bepalen,
dat x2 = p.
In dit geval is x dus middelevenredig tussen de straal van de cirkel (hier gelijk
aan 1) en het lijnstuk 2AR. Zie voor de constructie van de middelevenredige Voorbeeld 3 (op de pagina Passermeetkunde).
Mascheroni geeft echter de volgende benaderingsconstructie.
| figuur 4 | 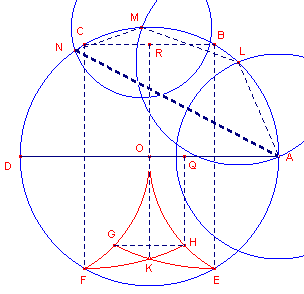 |
De punten B, C, D zijn op de gebruikelijke wijze geconstrueerd. E en F
zijn op dezelfde manier vastgelegd. Cirkel B(BE) bepaalt het punt G; cirkel C(CF) bepaalt het punt H. Deze beide cirkels snijden elkaar in K. Voorts zijn de punten L, M en N geconstrueerd, en wel zo, dat AL = LM = OK en MN = GH ------ (1). Nu is NA een benadering van de zijde x van het vierkant dat dezelfde oppervlakte heeft als de cirkel. Voor het "bewijs" hiervan gebruiken we nog twee punten: |
OR = �(OC2 - CR2)
= �(1 - �) = ��3.
In driehoek BKR is: KR = �(BK2 - BR2)
= �(3 - �) = ��11, immers BK =
BE = �3.
Dan is: OK = KR - OR = �(�11 - �3)
------ (2)
Driehoek ACH is gelijkbenig (CA = CH = �3). Hierin is:
cos CAH = �AH / AC = �/�3 = 1/6�3. Waaruit volgt dat sin CAH = 1/6�33.
cos OAH = cos(CAH - 30�) = 1/6�3 . ��3 + 1/6�33 . � = � + 1/12�33.
Nu is, omdat AH = 1, OQ = OA - AQ = OA - AQ/AH = 1 - cos OAH = � - 1/12�33 = 1/12(9
- �33), zodat
HG = 1/6(9
- �33) ------ (3)
Uit (1), (2) en (3) volgt nu
AL = LM = �(�11 - �3) en MN = 1/6(9
- �33).
| figuur 5 | 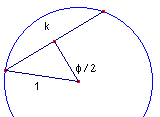 |
Met deze waarden kunnen de lengten van de bogen AL, LM en MN (bij een
straal van 1) gemakkelijk berekend worden. Zie figuur 5, waarin de booglengte gelijk is aan f en de lengte van de koorde gelijk is aan k. Dan is f = 2 arcsin k/2. |
Voor boog ALMN (in figuur 4) hebben we dan
bg ALMN = 4arcsin �(�11 - �3) +
2arcsin 1/12(9 - �33)
Voor het lijnstuk AN, dat deze boog opspant, geldt dus:
AN = 2 sin bg(ALMN)/2 = 2 sin ( 2arcsin �(�11 - �3) + arcsin 1/12(9
- �33) ) = 1,772656991.
De fout in de constructie is dan AN - �p = 0,0002031.
Bij een straal van 1 m is de fout dus ongeveer 0,2 mm.
Klik hier ![]() voor een CabriJavapplet
van deze constructie.
voor een CabriJavapplet
van deze constructie.
[passermeetk2.htm] laatste wijziging op: 16-02-04