Gulden snede en getallen van Fibonacci

Overzicht ][ Elementen | Meetkunde | Getallentheorie

Zie ook de pagina "Logaritmische spiraal".

Overzicht

1. Elementen
Euclides geeft in zijn Elementen op twee plaatsen een constructie voor het verdelen van een lijnstuk in uiterste en middelste reden, ook wel het aanbengen van de gulden snede (Latijn: sectio aurea of ook wel: proportio divina) genoemd.
Hij doet dit in Boek II (propositie 11 van de "rekenkundige meetkunde") en in Boek VI (propositie 30 van de "redentheorie"); op de pagina Boek II, Opmerking 3 staat ook een 'moderne' constructie (deze constructie staat hieronder als CabriJavapplet).

In het onderstaande geven we enkele andere toepassingen van de gulden snede.

2. Rekenen

2.1. Phi
Zij C het punt dat het lijnstuk AB verdeelt in uiterste en middelste reden.
We schrijven soms wel ter afkorting: C = vumr(AB); zie figuur 1.

figuur 1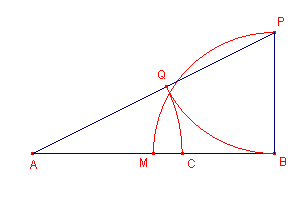

Stellen we BC = 1 en AC = x, dan is AB = x + 1. Dan volgt uit AB : AC = AC : BC, dat    (x + 1)/x = x / 1 zodat (1)......   x2 - x - 1 = 0

De positieve wortel van vergelijking (1) is x = (1 + �5)/2.
Deze (positieve) waarde van x wordt wel aangegeven met de Griekse letter f (Phi; de eerste letter van de naam van de Griekse beeldhouwer Phidias, 490(?)-430(?) vChr).
De negatieve waarde x = (1 - �5)/2 geven we aan met f '.
Nu is, in vijf decimalen, f  = 1.61803 en f ' = - 0.61803 (soms wordt ook de positieve waarde 0.61803 voor f ' gebruikt).

Klik hier >< voor een CabriJavapplet van bovenstaande constructie.
o Klik hier voor een tweede constructie.

Het grootste deel van de VUMR van AB is AC.
Nu is

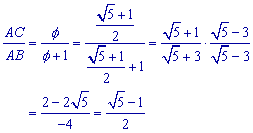
In figuur 1 is ook de constructie van het punt C aangegeven.
Constructiestappen:

Bewijs:
Zij AB = a. Dan is BM = PB = �a.
Volgens de stelling van Pythagoras in dan AP² = a² + �a² = 5/4a².
Nu is AQ = AC = (a�5)/2 - �a = a(�5 - 1)/2.
Zodat
AC/AB = (�5-1)/2,
waaruit volgt, dat voor C geldt C = vumr(AB). �

2.2. Verdere eigenschappen van Phi

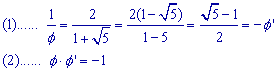
Verder blijkt uit de vergelijking x² - x - 1 = 0 en uit de berekende waarden van f en f ':

(4)...... Wegens hebben we voorts AB =  f . AC.

2.3. Constructie van een hoek van 36�

figuur 2		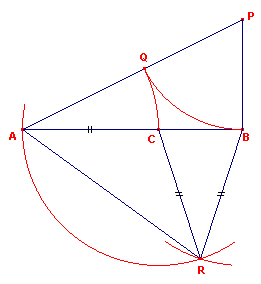In figuur 2 is voortgebouwd op de constructie van figuur 1. C = vumr(AB). Getekend zijn opvolgend: - Cirkel(C, CA) - Cirkel(B, CA). Een snijpunt van beide cirkels is het punt R. Nu is hoek BRC = 36�. (*) Het bewijs hiervan volgt door gebruikmaking van de eigenschap die volgt uit figuur 3. Klik hier >< voor een CabriJavapplet van deze constructie.
figuur 3		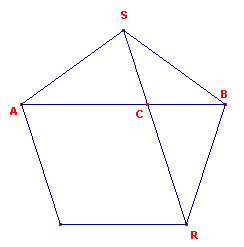In de regelmatige vijfhoek in figuur 3 hebben we: driehoek SBC ~ driehoek ABS, waaruit:    AB : SB = BS : BC of ook    AB : AC = AC : BC Het punt C verdeelt de diagonaal AB dus in uiterste en middelste reden. Anders geformuleerd: . Stelling In een regelmatige vijfhoek verdelen snijdende diagonalen elkaar in uiterste en middelste reden.

Hieruit volgt het bewijs van de constructie van de hoek van 36� in figuur 2. �

(*)
Voor een afleiding van de goniometrische verhoudingen van de hoeken van 36� en 72� zie het artikel "Over de hoeken van 36� en 72�", januari 2006.
Klik hier om het artikel te downloaden (PDF-bestand; ca. 112 kB).
Opmerking. Voor het lezen van een PDF-bestand wordt Adobe Reader^� geadviseerd >>> .

3. Het pentagram

3.1. Verband tussen �5 en de vijfhoek
Er is een onmiskenbaar verband tussen �5 en f, en dus ook tussen �5 en de regelmatige vijfhoek.
Hieronder geven we een (en dat is ��n van de vele) constructie van een regelmatige vijfhoek.

figuur 3.1a		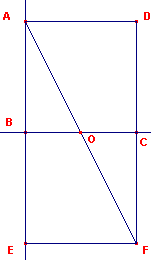We gaan uit van een rechthoek AEFD (dubbelvierkant) met zijden 1 en 2. De lengte van de diagonaal van die rechthoek is gelijk aan �5 (zie figuur 3.1.a). De lengte van het lijnstuk OA is dan dus ��5. Zie verder figuur 3.1b. We tekenen vervolgens de cirkel (B, BC). De lengte van de straal van die cirkel is 1. Deze cirkel is ook de omcirkel van de te construeren regelmatige vijfhoek.
figuur 3.1b		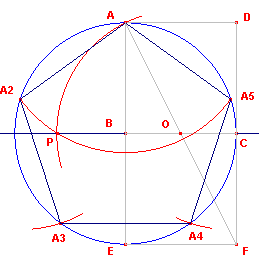De cirkel (O, OA) snijdt de drager van het lijnstuk BC in het punt P. De cirkel (A, AP) snijdt de omcirkel in de punten A2 en A5, samen met A hoekpunten van de regelmatige vijfhoek. De hoekpunten A3 en A4 kunnen we vinden met de cirkels (A2, AA2) en (A5, AA2). Klik hier >< voor een CabriJavapplet van deze constructie.

o Klik hier voor enkele andere constructies van de regelmatige vijfhoek.

3.2. Het pentagram en Phi

figuur 4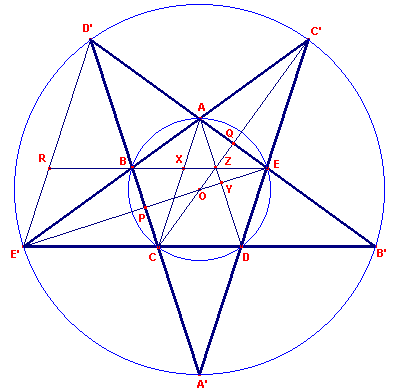

Het pentagram (vijfhoekige regelmatige ster) kan ontstaan door de zijden van een regelmatige vijfhoek twee aan twee te verlengen. We kiezen AB = 1 (de zijde van de regelmatige vijfhoek). Zijn R en r opvolgend de stralen van de omgeschreven cirkels van A'B'C'D'E' en ABCDE, dan kunnen we eenvoudig vinden: (i)     AD' = f (ii) OP/r = f / 2 (iii) OE'/r = f 2 (iv) OP/OE' = 2f (v) Een diagonaal zoals BE heeft lengte f. (vi) Is X het snijpunt van twee diagonalen AC edn BE, dan geldt:    EX / XB = f    CX / XA = f

4. Enkele (onvermoede) vindplaatsen van Phi

4.1. De 3-4-5-driehoek

figuur 5a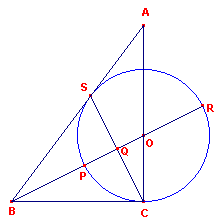

Driehoek ABC is rechthoekig in C. AC = 4, CB = 3 en AB = 5. De lijn door het hoekpunt B is de bissectrice van hoek B. Deze snijdt AC in het punt O. O is het middelpunt van de cirkel door het punt C. Omdat O op de bissectrice van B ligt, raakt deze cirkel ook aan AB (in het punt S). Dus: BS = 3 en AS = 2. De bissectrice snijdt de cirkel in de punten P en R en de lijn CS in Q (de hoek bij Q is recht). Volgens de bissectrice-stelling is BC/BA = CO/AO = 3/5 Dus CO = 3/8 . 4 = 3/2 (= straal) en AO = 5/2. Verdere berekeningen geven:

BO = 3/2�5 (via driehoek BCO), zodat
   BP = BO - PO = 3/2(�5 - 1)
   BR = BP + PR = 3/2(�5 - 1) + 3 = 3/2(�5 + 1)
Hieruit volgt dan
   BR / PR = (�5 + 1)/2 = f
Waaruit volgt, dat P = vmur(BR). �

figuur 5b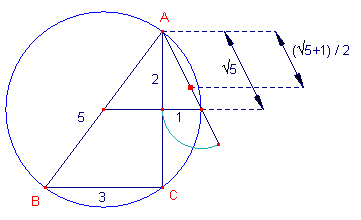

In nevenstaande figuur staat een andere constructie voor f in een 3-4-5-driehoek. De wijze van construeren spreekt voor zichzelf.

4.2. De macht van een punt

figuur 6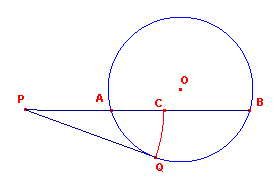

In figuur 6 is AB = PQ, waarbij PQ het raaklijnstuk is uit P aan de cirkel met middelpunt O. Nu geldt voor de macht van het punt P tov. cirkel O: PA x PB = PQ2, zodat PA : PQ = PQ : PB, of PA : AB = AB : (PA + AB) We zien dus, dat A = vumr(PB). Verder geldt voor het punt C, dat PC = PQ. Nu is:    PA = PC - AC = AB - AC en ook    BC = AB - AC, zodat    PA = BC

We hebben nu:
   AB : BC = AB : PA = f
Dus ook C = vumr(AB).

4.3. Goniometrie

We lossen de vergelijking sin 2x = cos 3x op.
Hieruit volgt direct:
   sin 2x = sin(p/2 - 3x)
zodat we (oa.) vinden x = p/10.
De vergelijking laat zich als volgt herleiden:

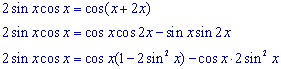
We laten de "trivale" oplossingen uit cos x = 0 voor wat ze zijn, zodat nu:

Hieruit vinden we dan als (positieve) oplossing:

zodat
   sin 18� = 1/(2f)
Wegens cos 36� = 1 - 2sin² 18� = 1 - 1/(2.Phi²), vinden we (na enige herleiding)
   cos 36� = f / 2

N.b.
Voor een afleiding van de goniometrische verhoudingen van de hoeken van 36� en 72� zie het artikel "Over de hoeken van 36� en 72�", januari 2006.
Klik hier om het artikel te downloaden (PDF-bestand; ca. 112 kB).

4.4. Phi als kettingbreuk
Op de pagina "Kettingbreuken" wordt een inleiding gegeven tot de theorie van de kettingbreuken.
Uit f ² = f + 1 volgt:
   f = 1 + 1 / f
en dus ook
   
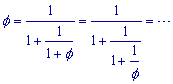
We vinden dus de oneindige kettingbreuk (zie de pagina "Kettingbreuken" voor de schrijfwijze):
   f = ]1, 1, 1, 1, 1, ...[
De benaderende breuken P_k/Q_k van f kunnen we nu via een algoritme berekenen:
   
Hierin zijn de getallen a_k de opvolgende waarden in ]a₁, a₂, ...[. Dus voor alle k hebben we in dit geval a_k = 1.

Zie voor de tellers en noemers van de benaderende breuken paragraaf  6. Getallen van Fibonacci.

Zie ook de pagina "Logaritmische spiraal".

4.5 Een ring en een ellips - gulden ellips

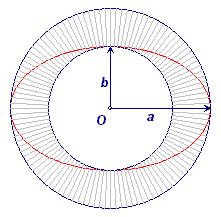We gaan uit van twee in O concentrische cirkels met stralen a en b (a > b). De oppervlakte van de ring is gelijk aan    pa2 - pb2 = p(a2 - b2) ......(1) De ellips met grote as gelijk aan 2a en kleine as gelijk aan 2b, en met O als middelpunt, heeft als oppervlakte    pab ......(2) Wanneer beide oppervlaktes gelijk zijn, vinden we uit (1) en (2):    a2 - b2 = ab    a2- ab - b2 = 0 waaruit we vinden dat a / b  = f Opmerking - We zouden zo'n ellips dan (bij gelijke oppervlaktes dus) een gulden ellips kunnen noemen.

5. Gulden rechthoek en gulden driehoek

5.1. Gulden rechthoek

figuur 7a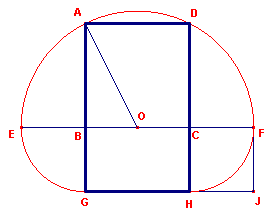

Uitgaande van een vierkant ABCD met zijde 1 construeren we de punten E en F via de cirkel O (het midden van BC) met straal OA (= ��5). Nu is EB = BG = CF = CH = ��5 - � = (�5 - 1)/2 = 1/f. Daardoor: AG = AB + BG  = 1 + 1/f = (f  + 1)/f = f. De zijden van rechthoek AGHD zijn dus 1 en f. We noemen een dergelijke rechthoek waarvan de zijden zich verhouden als 1 : f een gulden rechthoek.

Opmerkingen
[1]
V(BGJF) = (1 + 1/f)(1/f) = 1/f  + 1/f ² = (f + 1)/f ² = 1
[2]
Bovenstaande constructie van een gulden rechthoek is niet de meest eenvoudige. Hieronder staat de meest gebruikte

figuur 7b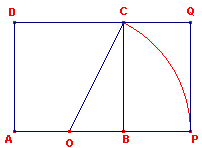

Uitgaande van vierkant ABCD met AB = 1 (O is het midden van AB) hebben we: OC = ��5. Met OP = CO hebben we dan AP = � + ��5. N.b. Op deze constructie kunnen we natuurlijk ook een constructie van de regelmatige vijfhoek baseren. Zie daarvoor de pagina "Een andere constructie van de gulden snede" (deze website). Zie verder ook Referentie [1].

[3]
Zie ook de pagina "Logaritmische spiraal", waarop in de gulden rechthoek via verdeling daarvan in een kleinere rechthoeken een spiraal kan worden getekend.
[einde Opmerkingen]

5.2. Gulden driehoek

figuur 8

Een driehoek met hoeken van 36�, 72� en 72� heet gulden driehoek. De bissectrice van hoek B snijdt de zijde AC in het punt D. Dan geldt AD = BD = BC. Nu is: ABC ~ BCD (hh), zodat AC : BD = BC : CD of AC : AD = AD : CD Zodat D = vumr(AC). Of ook: AC = f  . AD. Kiezen we BD = 1, dan is dus AC = AB = f.

Gevolg
We bekijken de oppervlaktes (V) van de verschillende driehoeken in figuur 8.
V(ABC) = �AB ^. AC ^. sinA = �f ²sin 36�
V(ABD) = �BA ^. BD ^. sinABD = � ^. f ^. 1 ^. sin 36� = �f sin 36�
V(BCD) = �BC ^. BD ^. sinCBD = � ^. 1 ^. 1 ^. sin 36� = � sin 36�
Zodat:
V(ABC) : V(ABD) : V(BCD) = f ² : f : 1.
[einde Gevolg]

Opmerking
Zie ook de pagina "Logaritmische spiraal", waarop in de gulden driehoek via verdeling daarvan in een kleinere driehoeken een spiraal kan worden getekend.
[einde Opmerking]

6. Getallen van Fibonacci
De (meetkundige) rij getallen
   1, f, f ², ...
heeft ook de additieve eigenschap u_n + 1 = u_n + u_n - 1 (met n = 2, 3, ...).
Dit volgt uit het feit, dat f ² = f + 1.
Zo is f ³ = f . f ² = f(f + 1) = f ² + f = 2f + 1
De rij kan dus ook geschreven worden als
   1, f, 1 + f, 1 + 2f, 2 + 3f, ...

Geven we u₁ en u₂, dan ligt de rij vast.
Twee voorbeelden:
[1]
u₁ = 2, u₂ = 1
Lucas-rij: 2, 1, 3, 4, 7, 11, ...
De getallen in deze rij heten Getallen van Lucas (Lucas-numbers; zie ook Referenties).
[2]
u₁ = 5, u₂ = 2
Lucas-rij: 5, 2, 7, 9, 16, 25, 41, 66, 107, 173, 280, 453, 733, ..., 13153, 21282, ...
We berekenen van deze rij voor enkele waarden van n de uitdrukking u_n+1/u_n:
   16 / 9 = 1,7777...
   453 / 280 = 1,6178...
   733 / 453 = 1,6181...
   21282 / 13153 = 1,61803...
We zien, dat de waarden van u_n+1/u_n de waarde van f  = (�5 + 1)/2 benaderen.
[einde Voorbeelden]

De rij van Fibonacci
We kiezen nu, als in de voorbeelden:
u₁ = 1, u₂ = 1
De eerste 40 termen van de bijbehorende Lucas-rij staan in de volgende tabel.

Deze elementen van deze rij heten getallen van Fibonacci (zo genoemd door Lucas in 1877).
Leonardo van Pisa (genaamd Fibonacci, Filius Bonaccii, wat "zoon van Bonaccio" betekent) leefde ca. 1175-1250.
Fibonacci publceerde in zijn boek Liber Abaci het befaamde "konijnenvraagtuk" waarvan de getallen van Fibonacci de oplossing zijn.
Ook voor de getallen van Fibonacci geldt, dat u_n+1/u_n de waarde van f  = (�5 + 1)/2 benaderen:
   u₁₅/u₁₄ = 1,618037
   u₂₅/u₂₄ = 1,618033
We kunnen bewijzen dat
   
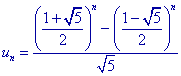
Klik hier voor een bewijs van de formule.
De formule werd het eerst gepubliceerd in 1730 door Abraham de Moivre (1667-1754, geboren in Vitry, Frankrijk).
De formule wordt echter vaak aangeduid als de formule van Binet (naar Jacques Philippe Marie Binet, 1786-1856, geboren in Rennes, Frankrijk). Binet bewees de formule in 1843.

We kunnen inderdaad ook bewijzen, dat

Klik hier voor een bewijs van deze stelling voor de rij van Fibonacci.

Opmerking
Een eenvoudig bewijs van de stelling voor de rij van Fibonacci kan ook worden geleverd door f  te ontwikkelen in een kettingbreuk.
Zie voor een aanzet daartoe paragraaf 4.4. Phi als kettingbreuk.
[einde Opmerking]

7. Referenties

Zie ook de pagina "Logaritmische spiraal".

- Referenties op Internet kunnen worden gevonden met de sleutelwoorden "golden section ratio fibonacci";
oa. over Lucas-numbers en Fibonacci-numbers (door R. Knott - Surrey University, Guildford, UK).

[sectioaurea.htm] laatste wijziging op: 16-02-10