Boek II
Inleiding | Prop II, 1-3 | Prop I, 4-7 | Gulden snede (Prop II-11) | Prop II-14
[ Elementen | DK & Meetkunde ]
1. Inleiding 
Het tweede Boek van de Elementen brengt, voortbouwend op propositie
I-43 (waarin het gnomon-theorema aan de orde komt) en de proposities
I, 44-47, de fundering aan voor wat we "rekenkundige meetkunde" of
"meetkundige rekenkunde" zouden kunnen noemen.
De betekenis ervan is als volgt kort te omschrijven: de theorie stelde de Griekse
wiskundigen in staat om zonder hulp van enige algebra (letterrekenen) tal van resultaten
te bereiken, die in onze tijd welhaast onafscheidelijk aan toepassing van algebraische
begrippen en methoden op de meetkunde verbonden lijken.
Het boek begin met twee terminologische definites:
Definities
(A) Men zegt, dat elk rechthoekig parallelogram omvat wordt door de twee rechte lijnen
die den rechten hoek omvatten.
(B) Laat in elk parallelogram een van de twee parallelogrammen om zijn diagonaal, samen
met de twee complementen, gnomon heeten. |
figuur 1 |
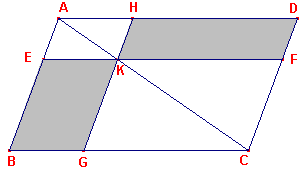 |
Zoals uit figuur 1 blijkt, kunnen in het parallelogram op de diagonaal AC twee
gnomons worden onderscheiden:
(i) ABG-K-FDA en (ii) CBE-K-HDF.
Als we de notatie van Euclides gebruiken, die een parallelogram aangeeft met een
diagonaal, dan zijn de bedoelde gnomons dus:
(i) AK-BK-DK en (ii) CK-BK-DK
Zonder problemen kunnen we een gnomon dus aangeven door middel van het
"voortbrengende" parallelogram:
(i) gnomon AK en (ii) gnomon CK. |
2. Proposities II, 1-3

Deze proposities zijn van weinig belang. Ze leggen niets anders vast dan optelling van
oppervlakten. Vandaar, dat we ze hier (vertaald uit Th. L. Heath, The Thirteen Books
of the Elements) zonder bewijs noemen.
Wel vermelden we het algebra?sch equivalent bij elke propositie.
Propositie II-1
Als er twee rechte lijnen zijn, en een van beide is verdeeld in een willekeurig aantal
delen, dan is de rechthoek omvat door de beide rechte lijnen gelijk aan de rechthoeken
omvat door de onverdeelde lijn en elk van de lijnstukken |
a(b + c + d + ...) = ab + ac + ad + ... |
Propositie II-2
Als een rechte lijn willekeurig wordt verdeeld, dan zijn de rechthoeken op de gehele
[lijn] en de beide delen gelijk aan het vierkant op de gehele lijn. |
(a + b)a + (a + b)b = (a + b)2 |
Propositie II-3
Als een rechte lijn willekeurig wordt verdeeld, dan is de rechthoek op het geheel en
een van de delen gelijk aan de rechthoek op de delen en het vierkant op het eerste deel. |
(a + b)a = a2 + ab |
|
3. De proposities II, 4-7 - bijzondere producten 
De eerste "belangrijke" propositie levert direct al een fraaie meetkundige
interpretatie van het uit algebra bekende bijzondere product
(a + b)2 = a2 + b2 + 2ab
De propositie is als volgt in Boek II verwoord:
Propositie II-4
Als een rechte lijn willekeurig wordt verdeeld, dan is het kwadraat op het geheel gelijk
aan de kwadraten op de delen en tweemaal de rechthoek op deze delen. |
Bewijs:
Want zij de rechte lijn AB willekeurige gedeeld in C.
Ik zeg dat het vierkant op AB gelijk is aan de vierkanten op AC, CB en tweemaal de
rechthoek op AC, BC.
| figuur 2 |
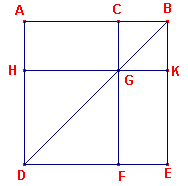 |
Want laat het vierkant ADBE beschreven zijn op AB, laat BD verbonden
zijn, door C laat CF getrokken zijn evenwijdig aan AD of EB, en door G laat HK getrokken
zijn evenwijdig aan AB of DE.
Dan is, omdat CF evenwijdig is aan AD en BD beide snijdt, de buitenhoek CGB gelijk aan de
oevreenkomstige binnenhoek ADB.
Maar de hoek ADB is gelijk aan de hoek ABD, omdat de zijde BA ook gelijk is aan AD. Daarom
is de hoek CGB ook gelijk aan de hoek GBC, zodat de zijde BC gelijk ook is aan de zijde
CG.
Maar CB is ook gelijk aan GK, en CG aan KB. Daarom is GK ook gelijk aan KB. Dus is CGKB
gelijkzijdig. |
Ik zeg verder dat deze ook rechthoekig is. Want, omdat CG evenwijdig is aan BK, zijn de
hoeken KBC, GCB gelijk aan twee rechte hoeken, zodat de binnenhoeken hoeken CGK, GKB ook
recht zijn.
Dus is CGKB rechthoekig. En er was bewezen, dat het ook gelijkzijdig was. Daarom is het
een vierkant; en het is beschreven op CB.
Om dezelfde reden is ook HF een vierkant; en het is beschreven op HG die gelijk is aan AC.
Daarom zijn de vierkanten HF, KC ook vierkanten op AC, CB.
Nu, omdat AG gelijk is aan GE, en AG de rechthoek AC, CB is, want GC is gelijk aan CB;
daarom is GE ook gelijkaan de rechthoek AC, CB.
Maar de vierkanten HF, CK zijn ook de vierkanten AC, CB; daarom zijn de vier
[oppervlakten] HF, CK, AG, GE gelijk aan de vierkanten op AC, CB en tweemaal de rechthoek
op AC, CB.
Maar HF, CK, AG, GE is de gehele ADEB, dat een vierkant is op AB.
Daarom is het vierkant op AB gelijk aan de vierkanten op AC, CB en tweemaal de
rechthoek op AC, CB.
Hetgeen te bewijzen was. ?
Opmerkingen
[1]
Propositie II-4 kan gemakkelijk worden uitgebreid to het geval waarin een rechte lijn
verdeeld is in meer dan twee stukken. Op dezelfde manier als hierboven kan dan een figuur
worden gemaakt waarin het algebra?sch equivalent
(a + b + c + ...)2 = a2 + b2 + c2 + ... + 2ab + 2ac + ... + 2bc + ...
is ge?llustreerd.
[2]
In het bovenstaande bewijs wordt door Euclides uitvoerig en zorgzaam
aandacht besteed aan het bewijs dat er sprake is van vierkanten op de diverse lijnstukken.
Ook in de op propositie II-4 volgende bewijzen is hiervan sprake.
Om zelf [dk] ook niet breedsprakig te worden beperken we ons in hetgeen volgt tot de kern
van het bewijs. Daarbij zullen we de volgende notaties (analoog aan die welke door Dr.
E.J. Dijksterhuis in De Elementen van Euclides zijn opgenomen):
oppervlakte van een rechthoek op zijden a en b:
R(a,b)
oppervlakte van een vierkant met zijde a: V(a)
oppervlakte van een parallelogram op zijden a en b:
P(a,b)
Voorts zij opgemerkt, dat we de oppervlakte van een parallelogram of rechthoek ook
(conform Euclides zelf) kunnen aangeven met een diagonaal.
[einde Opmerkingen]
Propositie II-5
Indien een rechte lijn verdeeld wordt in gelijke en ongelijke deelem, is de rechthoek,
omvat door de ongelijke deelen van het geheel, samen met het vierkant op het stuk tusschen
de deelpunten, gelijk aan het vierkant op de helft. |
Bewijs: (zie figuur 3 en opmerking 2
hierboven)
| figuur 3 |
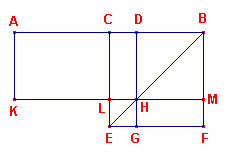 |
AB is het gegeven lijnstuk. C is het midden daarvan en D is een
willekeurig punt van AB.
Te bewijzen is dus: R(AD, DB) + V(CD) = V(BC)
Maak nu BM loodrecht op BD. Trek BH en voltooi V(BC). Nu is, wegens
AH = AL + CH = CM + HF:
R(AD, BD) = gnomon(BH) en ook
V(CD) = LG
Optelling van beide laatste resultaten geeft nu: R(AD, BD) + V(CD) = V(BC).? |
Opmerkingen
[1]
Stellen we AB = a en BD = x, dan kunnen we de propositie algebra?sch
formuleren als a (a - x) = rechthoek AH = gnomon BH.
Als nu dus de oppervlakte van gnomon BH bijvoorbeeld gelijk is aan b2,
dan kunnen we de vergelijking a (a - x) = b2
dus meetkundig oplossen.
[2]
Als we stellen, dat AD = a en BD = b, dan is AD = (a + b)/2
en CD = (a -b )/2. De propositie krijgt daardoor de volgende
algebra?sche vorm
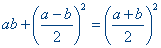
| Stellen we hierin a = m2 en b = 1 dan kunnen we
deze vergelijking herschrijven als |
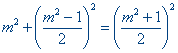 |
| Stellen we a = 2n2 en b = 2 dan gaat de
vergelijking over in |
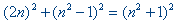 |
Hiermee krijgen we de regels van respectievelijk Pythagoras en Plato voor het vinden
van Pythagore?sche getaltripels.
[3]
Van deze propositie wordt onder andere gebruik gemaakt bij het bewijs van Prop. III-35.
[einde Opmerkingen]
Propositie II-6
Indien een rechte lijn middendoor wordt gedeeld en er wordt een rechte in rechte lijn
aan haar toegevoegd, dan is de rechthoek, omvat door de heele rechte met de toegevoegde en
de toegevoegde samen met het vierkant op de helft, gelijk aan het vierkant op de rechte,
bestaande uit de helft en de toegevoegde. |
Bewijs:
| figuur 4 |
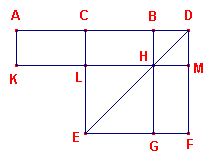 |
In figuur 4 is AB het gegeven lijnstuk, C het midden daarvan en D een
willekeurig punt op het verlengde van AB.
Nu is te bewijzen: R(AD, DB) + V(CB) = V(CD).
Maak DM loodrecht op BD en gelijk aan BD. Trek DH en voltooi het vierkant op CD.
Nu is, wegens AM = AL + CM = CH + CM = HF + CM:,
R(AD, DB) = gnomon(DH) en V(CB) = LG
Optelling van beide geeft dan R(AD, DB) + V(CB) = V(CD). ? |
Opmerkingen
[1]
Stellen we AB = a, BD = x en is b2 een gegeven
kwadraat (vierkant), dan kunnen we de propositie algebra?sch formuleren als
(a + x) x + (?a)2 = b2.
Hiermee hebben we dus een meetkundige oplossing van deze vierkantsvergelijking gevonden.
[2]
Stellen we AC = a en CD = b, dan hebben we
(a + b)(b - a) + a2 = b2
of (b + a)(b - a) = b2 - a2
Overigens, dit resultaat kon ook reeds uit propositie II-5 worden afgeleid.
[einde Opmerkingen]
Propositie II-7
Als een rechte lijn willekeurig verdeeld wordt, dan is het vierkant op het geheel en
dat op een van de delen samen gelijk aan tweemaal de rechthoek op het geheel en het eerste
deel en het vierkant op het andere deel. |
Bewijs:
| figuur 5 |
 |
In figuur 5 is AB een gegeven lijnstuk; C is een willkeurig punt daarvan.
Te bewijzen is nu: V(AB) + V(BC) = 2R(AB, BC) + V(AC).
Maak nu BE loodrecht op en gelijk aan AB. Nu is
2R(AB, BC) = gnomon(BG) + V(BC)
V(CA) = V(CA) ( = V(HG) )
Optelling van beide geeft
2R(AB, BC) + V(AC) = V(AB) + V(BC) ? |
Opmerking
We kunnen de vorm van de propositie iets wijzigen.Daarbij vatten we AB, BC op als twee
verschillende lijnstukken, waarvan AB groter is dan BC en AC als het verschil tussen beide
beide lijnstukken.
De propositie zegt dan, dat de vierkanten op de de lijnstukken samen gelijk zijn aan
tweemaal de rechthoek daarop en het vierkant op het verschil.
Algebra?sch vinden we dan, als we AB = a en BC = b stellen
a2 + b2 = 2ab + (a - b)2
of (a - b)2 = a2 + b2
- 2ab
[einde Opmerking]
4. Propositie II-11 - de gulden snede 
In propositie II-11 vermeldt Euclides voor de eerste keer het verdelen van een lijnstuk in
uiterste en middelste reden, de gulden snede. Hij doet dat voor de tweede keer in
Boek VI-30, waar hij daadwerkelijk de termen uiterste reden en
middelste reden gebruikt.
De term "gulden snede" (sectio aurea) is niet van klassieke oorsprong.
Volgens Tropfke, Geschichte der Elementarmathematik in sytematischer Darstellung mit
besonderer Ber?cksichtigung der Fachw?rter (2e Auflage, Berlin, 1923), treedt de
term voor het eerst op in 1835.
In boek II wordt de constructie dus, onafhankelijk van de in Boek VI behandelde redentheorie,
die de term reden pas mogelijk maakt, met behulp van de oppervlakterekening
uitgevoerd.
Propositie II-11
Een gegeven rechte zoo te verdeelen, dat de rechthoek, omvat door de heele rechte en
een der deelen, gelijk is aan het vierkant op het andere deel. |
We gegeven ook nu de constructie en het bewijs in verkorte vorm weer.
| figuur 6a |
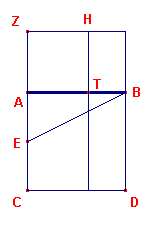 |
Zie figuur 6a.
Zij AB het gegeven lijnstuk.
Maak BD loodrecht op AB en gelijk aan AB. Trek AC en CD loodrecht op respectievelijk AB en
BD.
Kies E in het midden van AC. Maak EZ gelijk aan EB en daarna ZH gelijk aan ZA.
Trek tenslotte HT loodrecht op AB.
T is dan het gevraagde punt.Klik hier  voor een animatie van de
constructie. voor een animatie van de
constructie. |
Bewijs:
R(CZ, AZ) + V(AE) = V(EZ) volgens prop. II-6.
Wegens EZ = EB geldt dan ook
R(CZ, AZ) + V(AE) = V(EB).Met propositie I-47 (stelling van Pythagoras) vinden we dan, dat
V(EB) - V(AE) = V(AB) en , samen met AZ=HZ,
dat R(CZ, HZ) = V(AB) Door aftrekking van R(AT,AC) van beide vinden we dus dat
en dus dat R(DB, BT) = R(AB, BT) = V(AT). ?
Opmerkingen
[1]
Uit de constructie blijkt, dat het lijnstuk CZ door het punt A in middelste en uiterste
reden wordt verdeeld.
Immers, R(CZ, ZA) = V(AC).
[2]
Deze constructie kan worden opgevat als een bijzondere vorm van hyperbolische
aanpassing met kwadratisch exces, namelijk die waarin het aan te passen oppervlak gelijk
is aan het vierkant op het lijnstuk AB.
Zie voor een een behandeling van de hyperbolische aanpassing de betreffende pagina over Boek VI.
[3]
Een "moderne" constructie van de verdeling van het lijnstuk AB = a
in uiterste en middelste reden verloopt als volgt (zie figuur 6b).
| figuur 6b |
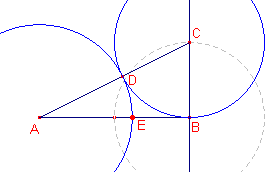 |
- Construeer het punt C zodat CB loodrecht staat op AB en CB = ? a.
- Bepaal het snijpunt D van AC met de cirkel (C, CB).
- Bepaal het snijpunt E van AB met de cirkel (A, AD). E verdeelt het lijnstuk AB nu in
uiterste en middelste reden.
Klik hier  voor een animatie van deze constructie.
voor een animatie van deze constructie. |
Bewijs: AC = ?(a2
+ 1/4 a2) = ? a?5
CD = 1/2a, dus AD = ? a?5 - ? a.
AE = AD, dus AE = ? a(-1 + ?5).
Deze oplossing kunnen we algebra?sch vinden door AE = x te stellen; dan is BE = a
- x.
Nus is AB : AE = AE : BE, of x2 = a(a - x);
zodat x2 + ax - a2 = 0.
AE is dus gelijk aan de positieve oplossing van deze vierkantsvergelijking. ?
[4]
Zie ook de pagina "Gulden snede en Getallen van Fibonacci"
[einde Opmerkingen]
5. Propositie II-14 - oplossing van x2 = ab

Propositie II-14 is de laatste propositie in Boek II.
Ook hierin is sprake van een existentiebewijs: het is mogelijk om een vierkant te
construeren waarvan de oppervlakte gelijk is aan de oppervlakte van een gegeven vierhoek.
Propositie II-14
Een vierkant te construeren, gelijk aan een gegeven rechtlijnige figuur. |
De (willekeurige) vierhoek wordt allereerst volgens propositie
I-45 (Boek I) equivalent getransformeerd in een rechthoek BD (zie figuur 7).
| figuur 7 |
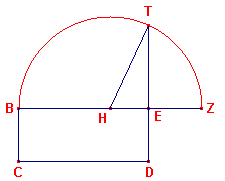 |
Is hierin BE > ED, dan maakt men EZ = ED (op het verlengde van BE) en
trekt de halve koorde ET in de cirkel op de middellijn BZ.
TE is dan de zijde van het gezochte vierkant.Dit is dus de gebruikelijke constructie
van de middenevenredige van twee lijnstukken uit de hedendaagse planimetrie.
Klik hier voor een "modern" bewijs
daarvan.
Bewijs: Volgens propositie II-5 is nu
R(BE, EZ) + V(HE) = V(HZ) |
Volgens propositie I-47 (stelling van Pythagoras) is V(TE) + V(HE) = V(HT).
Wegens HT = HZ hebben we nu
R(BE, EZ) = V(HZ) - V(HE) = V(HT) - V(HE) = V(TE). En dus wegens EZ = ED:
R(BE, ED) = V(TE). ?
Opmerkingen
[1]
We zouden het bewijs "modern" kunnen opschrijven als
| BE . EZ + HE2 |
= HZ2 volgens propositie II-5 |
|
= HT2 |
|
= HE2 + TE2; dus TE2 = BE . EZ |
[2]
Kiezen we BE = a, BC = b en TE = x, dan hebben we dus in
algebra?sche notatie: x2 = ab.
Bovenstaande constructie geeft dus een meetkundige oplossing van deze vergelijking.
[3]
In La G?om?trie van Descartes komt bovenstaande constructie eveneens voor.
Hieronder staat de tekst uit de (Utrechtse) vertaling van J.H. Glazemaker (Renatus Des Cartes, De Meetkunst,
1659).
.gif)
Zie verder ook: www.Wiskonst.nl
(klik op 'Originelen) of GMFW-Bronnen (fragment, Radbout Universiteit, Nijmegen)
[einde Opmerkingen]

[propII.htm] laatste wijziging op: 03-12-2007



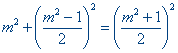




.gif)