Proposities I-33, I-34, I-35,
I-36, I-37
Inleiding | prop I-33 | prop I-34 | prop I-35 | prop I-36 | prop I-37 | Gnomon-theorema (Prop I-43)
[ Elementen | DK
& Meetkunde ]
1. Inleiding
Propositie I-33 is eigenlijk de inleiding tot de theorie van de equivalentie
van oppervlakten. Het begrip oppervlakte wordt echter niet door Euclides
gehanteerd.
Hij gebruikt in de onderstaande proposities het woord "gelijk" in de betekenis
van "heeft gelijke oppervlakte".
In de proposities I-4 en 24-26 (niet opgenomen op deze website) behandelt Euclides enkele
van de gebruikelijke congruentiekenmerken voor driehoeken, waarbij hij echter geen melding
maakt van de gelijke oppervlakten van congruente figuren.
2. De eerste
proposities over parallelogrammen
Propositie I-33
De rechten, die gelijke en parallelle rechten aan dezelfde zijden verbinden, zijn ook
zelf gelijk en parallel. |
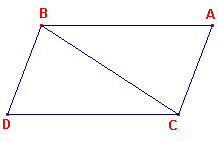
Laten AB, CD gelijk en parallel zijn, en laat de rechte lijnen AC, BD deze verbinden in
dezelfde richting (zie figuur 1).
Ik zeg dat AC, BD ook gelijk zijn en parallel.
| figuur 1 |
 |
|
Laat BC getrokken zijn.
Dan zijn, omdat AB parallel is met CD, en BC deze snijdt, de verwisselende hoeken ABC, BCD
aan elkaar gelijk [propositie I-29].
En, omdat AB gelijk is aan CD en BC gemeenschappelijk is, zijn de twee zijden AB, BC
gelijk aan de twee zijden DC, CB; en de hoek ABC is gelijk aan de hoek BCD. |
Daarom is de basis AC gelijk aan de basis BD, en de driehoek ABC is gelijk aan de
driehoek DCB, en de overblijvende hoeken zullen gelijk zijn aan de [andere] overgebleven
hoeken, namelijk die welke op de zijden staan [propositie I-4].
Daarom is de hoek ACB gelijk aan de hoek CBD.
En omdat de rechte lijn BC die de twee rechte lijnen AC, BD snijdt, de verwisselende
hoeken aan elkaar gelijk maakt, is
AC parallel aan BD;
en er was reeds bewzen dat ze aan elkaar gelijk zijn.
Hetgeen bewezen moest worden. ?
Propositie I-34
In parallel-lijnige oppervlakken zijn de overstaande zijden en hoeken aan
elkaar gelijk en de diagonaal deelt ze middendoor. |
Opmerking
In deze propositie komt voor het eerst het woord parallelogram (parallhlogrammon) voor, echter nog als bijvoeglijk naamwoord bij
oppervlakte (cwrion).
In de volgende propositie (I-35) wordt het woord voor het eerst zelfstandig gebruikt.
Vandaar dat er hier eerst nog vertaald is met "parallel-lijnig".
Wellicht valt het de lezer op, dat "parallelogram" geschreven wordt in plaats
van het gebruikelijke(?) "parallellogram"..
[einde Opmerking]
Laat ACDB een parallel-lijnig oppervlak zijn, en BC een diagonaal.
Ik zeg nu, dat de overstaande zijden en hoeken van het parallelogram ACDB aan elkaar
gelijk zijn, en dat de diagonaal het oppervlak in twee gelijke delen verdeelt.
| figuur 2 |
 |
Want, omdat AB parallel is aan CD, en de lijn BC beide snijdt, de
verwisselende hoeken ABC, BCD zijn gelijk [propositie I-29].
En ook, omdat AC parallel is aan BD en de lijn BC beide snijdt, zijn de verwisselende
hoeken ACB, CBD aan elkaar gelijk.
Daarom zijn ABC, DCB twee driehoeken waarvan de twee hoeken ABC, BCA opvolgend gelijk zijn
aan de hoeken DCB, CBD, en een zijde gelijk aan een zijde, namelijk de aanliggende zijde
aan de gelijke hoeken en een gemeenschappelijke zijde, BC. |
Daarom zijn ook de overblijvende zijden gelijk aan opvolgend de overblijvende zijden,
en de overblijvende hoek aan de overblijvende hoek;
dus de zijde AB is gelijk aan CD en AC aan BD.
En verder is de hoek BAC gelijk aan de hoek CDB.
En omdat de hoek ABC gelijk is aan de hoek BCD, en de hoek CBD aan de hoek ACB, is de hele
hoek ABD gelijk aan de hele hoek ACD.
En reeds bewezen is, dat de hoek BAC gelijk is aan de hoek CDB
Daarom zijn in parallel-lijnige oppervlakken de tegenoverliggende zijden en hoeken aan
elkaar gelijk.
Ik zeg vervolgens dat de diagonaal het oppervlak in twee gelijke delen deelt.
Want omdat AB gelijk is aan CD en BC gemeenschappelijk is, zijn de twee zijden AB, BC
gelijk aan opvolgend de zijden DC, CB; en de hoek ABC is gelijk aan de hoek BCD; daarom is
de basis AC ook gelijk aan DB en de driehoek ABC is gelijk aan de driehoek DCB.
Daarom deelt de diagonaal het parallelogram ACDB in gelijk delen.
Hetgeen te bewijzen was. ?
Propositie I-35
Parallelogrammen op dezelfde basis en tusschen dezelfde parallellen zijn gelijk aan
elkaar. |
Laten ABCD, EBCF parallelogrammen zijn op dezelfde basis BC en dezelfde parallellen AF,
BC.
Ik zeg dat ABCD gelijk is aan het parallelogram EBCF.
Want, omdat ABCD een parallelogram is, is AD gelijk aan BC.
Om dezelfde reden is ook EF gelijk aan BC, zodat AD gelijk is aan EF; en DE is
gemeenschappelijk.; dus is de gehele AE gelijk aan de gehele DF.
Maar AB is ook gelijk aan DC [prop. I-34]. dus zijn de twee zijden EA,
AB opvolgend gelijk aan de twee zijden FD, DC. en de hoek FDC is gelijk aan de hoek EAB,
de buitenhoek gelijk aan de binnenhoek [prop. I-29] |
figuur 3 |
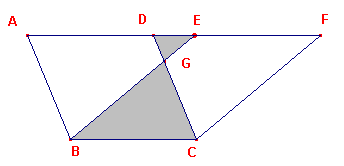 |
Daarom is de basis EB gelijk aan de basis FC, en de driehoek EAB zal gelijk zijn aan de
driehoek FDC [in de Griekse tekst staat DFC].
Laat DGE afgetrokken worden van elk. daarom is het trapezium ABGD, dat overblijft, gelijk
aan het trapezium EGCF, dat overblijft.
Wordt nu driehoek GBC bij beide opgeteld, dan is het hele parallelogram ABCD gelijk aan
het gehele parallelogram EBFC.
Hetgeen te bewijzen was. ?
Opmerkingen
[1] Euclides gaat voorbij aan het feit, dat AD en EF ook gedeeltelijk kunnen samenvallen.
Voorts leidt hij blijkbaar uit de tekening af, dat in het door hem beschouwde geval
(waarbij AD en EF geen gemeenschappelijk punt hebben) BE en CD elkaar snijden in een punt
(G) dat tussen de evenwijdige lijnen ligt.
[2] Propositie I-35 is de eerste zogenoemde locus-stelling (stelling waarin
sprake is van een meetkundige plaats; Proclus noemt dit een topikon qewrhma):
We citeren Proclus:
Ik noem die [stellingen] locus-stellingen waarin dezelfde
eigenschap bestaat op het geheel van een of andere locus, en [ik noem] een locus een
positie van een lijn of een oppervlak die ??n en dezelfde eigenschap voortbrengt.
In moderne terminologie zouden we propositie I-35 kunnen formuleren als:
De meetkundige plaats (verzameling) van zijden van parallelogrammen die dezelfde basis
hebben en gelijke oppervlakte, is een lijn evenwijdig met die basis.
[einde Opmerking]
Klik hier  voor een animatie van propositie I-35.
voor een animatie van propositie I-35.
Klik hier  voor animatie
van propositie I-35 die gebaseerd is op aanvullig tot een rechthoek.
voor animatie
van propositie I-35 die gebaseerd is op aanvullig tot een rechthoek.
Propositie I-36
Parallelogrammen op gelijke bases en tusschen dezelfde parallellen zijn gelijk aan
elkaar. |
Opmerking
Vergelijkend met propositie I-35 staat er hier gelijke bases in plaats van dezelfde
basis.
[einde Opmerking]
| figuur 4 |
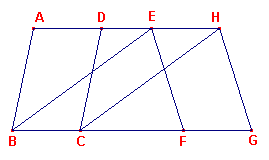 |
Zijn ABCD, EFGH parallelogrammen die op gelijke bases BC, FG staan, en
tussen dezelfde parallelen AH, BG vallen.
Ik zeg dat het parallelogram ABCD gelijk is aan EFGH.Want laat BE, CH verbonden zijn.
Dan, omdat BC gelijk is aan FG, terwijl FG gelijk is aan EH, is BC ook gelijk aan EH.
Maar ze zijn ook parallel. |
En EB, HC zijn ermee verbonden.
Maar rechte lijnen die gelijke en evenwijdige rechte lijnen in dezelfde richting
verbinden, zijn gelijk en parallel [prop. I-33].
Daarom is EBCH een parallelogram [prop. I-34].
En het is gelijk aan ABCD; want het heeft dezelfde basis BC ermee, en het ligt tussen
dezelfde paralellen BC, AH [prop. I-35].
Om dezelfde reden is ook EFGH gelijk aan dezelfde EBCH; zodat het parallelogram ABCD
gelijk is aan EFGH [prop. I-35].
Hetgeen te bewijzen was. ?
Propositie I-37
Driehoeken op dezelfde basis en tusschen dezelfde parallellen zijn gelijk aan elkaar. |
Zijn ABC, DBC driehoeken op dezelfde basis BC en tussen dezelfde parallellen AD, BC.
Ik zeg dat de driehoek ABC gelijk is aan de driehoek DBC.
| figuur 5 |
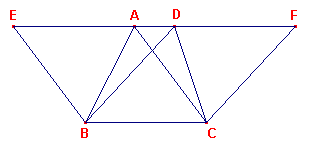 |
Laat AD verlengd zijn in beide richtingen tot E, F; door B zij BE
getrokken evenwijdig met CA; en door C zij CF getrokken evenwijdig met BD.
Dan is elk van de figuren EBCA, BDCF een parallelogram; en ze zijn gelijk, want ze staan
op dezelfde basis BC en tussen dezelfde paralellen BC, EF [prop I-35]. |
Verder is de driehoek ABC de helft van het parallelogram EBCA; want de diagonaal AB
deelt het in twee gelijke stukken [prop. I-34].
En de driehoek DBC is de helft van het parallelogram DBCF; want de diagonaal DC deelt het
in twee gelijke stukken [prop. I-34].
Maar de helften van gelijke dingen zijn gelijk aan elkaar.
Daarom is de driehoek ABC gelijk aan de driehoek DBC.
Hetgeen te bewijzen was. ?
3. Gnomon-theorema
Voor alle toepassingen van de equivalentie-theorie is de volgende propositie van
fundamenteel belang.
Propositie I-43
In elk parallelogram zijn de complementen van de parallelogrammen om de diagonaal aan
elkaar gelijk. |
Opmerking
Euclides geeft een parallelogram ABCD soms aan met parallelogram AC (dus
alleen via een aanduiding van de diagonaal).
| figuur 6 |
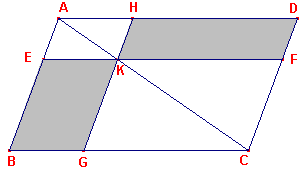 |
Onder het complement van een parallelogram AK om een diagonaal verstaat
hij (zie figuur 6) de parallelogrammen BK en KD.
Deze complementen ontstaan dus uit de door K (een punt van de diagonaal van een
parallelogram) getrokken lijnen evenwijdig met de zijden van dat parallelogram.
Beide zijn dus het complement van AK of van KC. |
[einde Opmerking]
Zij ABCD een parallelogram, en AC zijn diagonaal; en rond AC zijn EH en FG
parallelogrammen, en BK, KD de zogenoemde complementen.
Ik zeg dat het complement BK gelijk is aan het complement KD.
Want, omdat ABCD een parallelogram is, en AC zijn diagonaal, is de driehoek ABC gelijk
aan de driehoek ACD [prop. I-34].
Ook, omdat EH een parallelogram is, en AK zijn diagonaal, is de driehoek AEK gelijk aan de
driehoek AHK.
Om dezelfde reden is de driehoek KFC gelijk aan de driehoek KGC.
Nu, omdat de driehoek AEK gelijk is aan de driehoek AHK, en KFC gelijk aan KGC, is de
driehoek AEK samen met KGC gelijk aan de driehoek AHK samen met KFC.
En de gehele driehoek ABC is ook gelijk aan de gehele driehoek ADC.
Daarom is het complement BK, dat overblijft, gelijk aan het complement KD, dat overblijft.
Hetgeen te bewijzen was. ?
Opmerking
| figuur 7 |
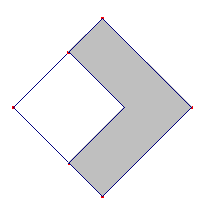 |
De naam gnomon-theorema komt voor het eerst voor bij enkele
Italiaanse schrijvers. (teorema del gnomone).
De gnomon was van oorsprong een astronomisch instrument, maar later werd de naam ook
gebruikt voor een instrument, dat diende om rechte hoeken te tekenen (het bestond uit twee
even lange dwars op elkaar gelegde latjes met een gemeenschappelijk hoekpunt).
Hieruit kan de meetkundige betekenis van gnomon worden afgeleid voor een meetkundige
figuur die van een vierkant overblijft als er een kleiner vierkant wordt afgenomen (zie
figuur 7). |
Euclides definieert het begrip gnomon aan het begin van Boek II, daarmee enige
uitbreiding gevend aan het begrip,
Laat in elk parallelogram ??n van de twee parallelogrammen om zijn diagonaal,
samen met de twee complementen, gnomon heten.
[einde Opmerking]

[propI33.htm] laatste wijziging op: 04-07-2001





