Indien een rechte, twee rechten treffende, de verwisselende binnenhoeken aan elkaar gelijk maakt, zullen de rechten aan elkaar parallel zijn.
prop 1-27 | pro I-28 | prop I-29 | Playfair's axioma ][ Elementen | Axioma van Wallis | DK & Meetkunde
| Propositie I-27 Indien een rechte, twee rechten treffende, de verwisselende binnenhoeken aan elkaar gelijk maakt, zullen de rechten aan elkaar parallel zijn. |
Want laat de rechte lijn EF twee rechte lijnen AB, CD snijden waarbij de verwisselende
binnenhoeken AEF, EFD aan elkaar gelijk zijn (zie figuur 1).
Ik zeg dat AB evenwijdig is met CD.
| figuur 1 | 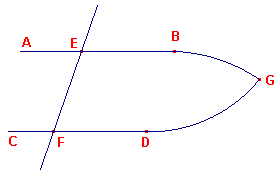 |
Want, als dat niet het geval is, zullen AB, CD bij verlenging snijden in
de richting van B,D of in de richting van A,C. Stel ze worden verlengd in de richting
van B,D en snijden in G. |
Op dezelfde manier kan bewezen worden dat ze elkaar niet snijden in de richting van A,C.
Maar rechte lijnen die elkaar niet snijden, in beide richtingen, zijn evenwijdig [def. 23];
daarom is AB evenwijdig met CD.
Hetgeen te bewijzen was. ?
? Klik hier ![]() voor een animatie
van propositie I-27.
voor een animatie
van propositie I-27.
? Zie ook de pagina
"Over evenwijdige lijnen"
In propositie I-28 van de Elementen geeft Euclides nog twee
andere criteria waaruit evenwijdigheid van lijnen kan worden geconcludeerd. Elk van deze
kan worden teruggebracht tot de andere. Vermoedelijk heeft Euclides aan de theorie omtrent
evenwijdige lijnen alleen de formulering het 5e postulaat toegevoegd (Heath, vol.
1, pag. 308).
Want laat de rechte lijn EF, die de twee rechte lijnen AB, CD treft, de buitenhoek EGB
gelijk maken aan den verwisselende binnenhoek GHD, of de binnenhoeken aan dezelfde zijde,
namelijk BGH, GHD, gelijk maken aan twee rechte hoeken.
Ik zeg dat AB parallel is aan CD.
| Want, omdat de hoek EGB gelijk is aan de hoek GHD, terwijl de hoek EGB
gelijk is aan de hoek AGH [prop. 1-15; overstaande hoeken; dk], de hoek AGH is ook gelijk
aan de hoek GHD; en ze zijn verwisselend. Daarom is AB parallel aan CD [prop. 1-27]. |
figuur 2 | 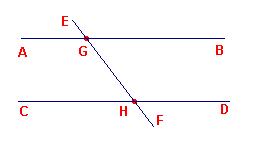 |
Weer, omdat de hoeken BGH, GHD gelijk zijn aan twee rechte hoeken, en de hoeken AGH,
BGH ook gelijk zijn aan twee rechten hoeken [prop. 1-13; nevenhoeken; dk], zijn de hoeken
AGH, BGH gelijk aan de hoeken BGH, GHD.
Trekken we nu BGH van elk af; dan is de oveblijvende hoek AGH gelijk aan de overbljvende
hoek GHD; en ze zijn verwisselend.
Daarom is AB parallel aan CD [prop. 1-27]
Hetgeen te bewijzen was. ?
De eerste 28 proposities in de Elementen hangen niet af van het 5e postulaat. Propositie 29 is dus de
eerste propositie die daar wel van afhangt.
Want laat de rechte lijn EF de lijnen AB, CD treffen.
Ik zeg dat daardoor de verwisselende hoeken AGH, GHD gelijk zijn, dat de buitenhoek EGB
gelijk is aan de binnenhoek overeenkomstige binnenhoek, en dat de buitenhoeken aan
dezelfde zijde, gelijk zijn aan twee rechte hoeken.
| figuur 3 |  |
Want, als de hoek AGH ongelijk is aan de hoek GHD, is ??n van beide
groter. Zij de hoek AGH de grootste. Laat de hoek BGH bij elk worden opgeteld.; dan zijn de hoeken AGH, BGH groter dan de hoeken BGH, GHD. Maar de hoeken AGH, BGH zijn gelijk aan twee rechte hoeken [prop. 1-13; nevenhoeken; dk]; dus de hoeken BGH, GHD zijn minder dan twee rechte hoeken. |
Maar rechte lijnen die oneindig verlengd worden vanuit hoeken die minder dan twee rechte hoeken, snijden elkaar [postulaat 5]; dus AB, CD, al oneidndig verlengd, snijden elkaar; maar ze snijden elkaar niet, omdat ze bij onderstelling parallel zijn.
Daarom is de hoek AGH niet ongelijk aan de de hoek GHD; dus is daarom eraan gelijk.
Opnieuw, de hoek AGH is gelijk aan de hoek EGB [prop. 1-15; overstaande hoeken; dk];
daarom is de hoek EGB gelijk aan de hoek GHD.
Laat de hoek BGH bij beide opgeteld worden.; dan zijn de hoeken EGB, BGH gelijk aan de
hoeken BGH, GHD.
Maar de hoeken EGB, BGH zijn gelijk aan twee rechte hoeken [prop. 1-13, nevenhoeken; dk];
dus zijn de hoeken BGH, GHD gelijk aan twee rechte hoeken
Hetgeen te bewijzen was. ?
Playfair's axioma ![]()
We noemden bij de eerste behandeling reeds dat Euclides' 5e postulaat
| En [laat ge?ist zijn] dat, als een rechte, die twee rechten treft, de binnenhoeken aan dezelfde kant kleiner dan twee rechte [hoeken] maakt, de twee rechten, tot in het oneindige verlengd, elkaar ontmoeten aan de kant, waar de hoeken kleiner zijn dan twee rechte [hoeken]. |
vervangen kan worden door
| Door een punt buiten een rechte gaat precies ??n rechte lijn die met die rechte parallel is. |
Deze formulering is afkomstig van John Playfair (1748-1819, Schotland), hoewel ook Proclus (Proclus Diadochus, 410-485, Griekenland) dit alternatief noemt.
In 1795 publiceerde Playfair het axioma in zijn boek The first six books of Euclid
with two books on the geometry of solids.
In een herdruk van dit boek (New York, 1819)
vinden we (echter) als axioma XI
| Two straight lines which intersect one another, can not be both parallel to the same straight line. |
2e Bewijs van Propositie I-29:
We bewijzen dat de verwisselende binnenhoeken AGH, GHD gelijk zijn.
Als ze niet gelijk zijn, dan trekken we door G de lijn KL die KGH gelijk maakt aan de hoek
GHD.
| figuur 4 | 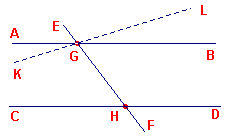 |
Dan, omdat de hoeken KGH, GHD gelijk zijn, is KL parallel aan CD [prop. I-27]. Dus zijn er twee lijnen KL, AB door G, die beide parallel zijn met de rechte lijn CD: hetgeen onmogelijk is (vanwege Palyfair's axioma). Dus kan de hoek AGH niet ongelijk zijn aan de hoek GHD. ? |
We zullen nu de volgende stelling bewijzen.
| Stelling Uit Playfair's axioma volgt Euclides' vijfde postulaat |
Bewijs: Zijn AB, CD lijnen die met de transversaal EF de hoeken AEF, EFC maken die samen kleiner zijn dan twee rechte hoeken (zie figuur 5).
| figuur 5 | 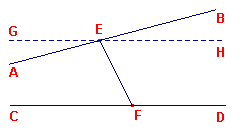 |
We zullen aantonen, dat AB, CD elkaar snijden in de richting van A, C. Trek
door E een lijn GH die met EF de hoek GEF maakt die gelijk is aan EFD. |
Want, als dat niet zo is, dan moet AB parallel zijn met CD; in dit geval hebben we twee lijnen A. GH door E die beide parallel zijn met CD: hetgeen onmogelijk is (axioma van Playfair).
Dus AB en CD snijden elkaar.
(2) Omdat AB. CD elkaar snijden, moeten ze een driehoek vormen met EF. Maar in elke
driehoek zijn twee hoeken samen steeds kleiner dan twee rechte hoeken. Dus zijn de hoeken
AEF, EFD (die samen kleiner zijn dan twee rechte hoeken) de hoeken van die driehoek; en
niet de hoeken BEF, EFD (die samen groter zijn dan twee rechte hoeken [als gevolg van
prop. 1-13; overstaande hoeken; dk].
Dat wil zeggen, dat EA, FC snijden elkaar in de richting van A, C oftewel aan de kant van
EF waarbij de hoeken kleiner zijn dan twee rechte hoeken. ?
Opmerkingen
[1]
In de meeste meetkunde-leerboeken gebruikt(e?) men meestal het axioma van Playfair in
plaats van dat van Euclides. Daarmee wordt dan eerst propositie I-29
bewezen, om vervolgens (indien gewenst) daaruit het 5e postuaat te laten volgen
[2]
Zie ook de pagina "Axioma van Wallis"
Zie ook de pagina "Over evenwijdige lijnen".
[einde Opmerkingen]