In Boek VI wordt de redentheorie (de leer der evenredigheden) die opgezet is in Boek V, toegepast op de meetkunde.
Het boek heeft de volgende opbouw
Boek VI
Overzicht | Aanpassing | Exces en defect | Gulden snede | Uitgebreide
Stelling van Pythagoras
[ Elementen | Meetkunde ]
1. Overzicht van Boek VI ![]()
In Boek VI wordt de redentheorie (de leer der evenredigheden) die opgezet is in Boek V,
toegepast op de meetkunde.
Het boek heeft de volgende opbouw
Prop VI, 1-3 : evenredigheid van rechten
Prop VI, 4-8 : gelijkvormigheid van driehoeken
Prop VI, 9-13 : constructies
Prop VI, 14-23 : verband tussen oppervlaktentheorie en redentheorie
Prop VI, 24-30 : uitbreiding van de oppervlakterekening met behulp van de redentheorie
Prop VI, 31 : Uitgebreide Stelling van Pythagoras
De proposities 1-23 komen in sterke mate overeen met de stellingen die in de moderne
planimetrie over deze onderwerpen worden behandeld. Om deze reden laten we ze op deze
pagina danook weg.
Ook de overige proposities zullen we niet in extenso behandelen. Slechts die proposities
die een bijzonder licht kunnen werpen op de meetkunde (in het huidige voortgezet onderwijs
in Nederland) en op de algebra, worden aan de orde gesteld.
2. Aanpassing
van oppervlakten ![]()
De Grieken pasten bij het veranderen van oppervlakten in principe een drietal operaties
toe die we hieronder zullen aangeven met hyperbolische, elliptische en parabolische
aanpassing van de oppervlakte.
De betekenis van die operaties vinden we eigenlijk terug in het commentaar van Proclus (411-485, GRiekenland) op de Elementen:
"Indien gij, wanneer een rechte lijn is uitgezet, het gegeven oppervlak langs de geheele rechte als zijde uitstrekt, zegt men, dat ge dat oppervlak [langs de lijn] aanpast.[paraballein] ; indien gij de lengte van het oppervlak grooter maakt dan de rechte zelf, dan zegt men dat het uitsteekt [uperballein]; indien gij haar kleiner maakt, zoodat er, wanneer het oppervlak beschreven is, iets van de rechte uitsteekt, dat het te kort schiet [elleipein]."
De meest vruchtbare toepassing van deze theorie vindt men voor het eerst in de leer der kegelsneden (Konica van Apollonios).
Ter verduidelijking vertalen we de bovenbedoelde terminologie door parabolische, hyperbolische en elliptische aanpassing. Op grond van de toepassingen die ervan bestaan, kunnen we de volgende definities geven:
De parabolische aanpassing is geheel gedefinieerd volgens en uitvoerbaar met behulp van
de Proposities I, 44-45. Deze proposities leren, dat als X is een gegeven oppervlak is en a
een gegeven lijnstuk, er een lijnstuk x te vinden is zodat de oppervlakte van het
parallelogram op a en x gelijk is aan X, en dit alles bij een gegeven
hoek j.
We zullen deze gelijkheid van oppervlakte in hetgeen volgt noteren als P(a, x)
= X.
Opmerking
Denken we ons X in de vorm van een parallelogram P(m, n) met dezelfde
hoek als waarin de aanpassing moet worden uitgevoerd, dan is het moderne equivalent van de
parabolische aanpassing blijkbaar de constructie van het lijnstuk x, bij een
gegeven lijnstuk a, waarvan de lengte voldoet aan de betrekking x = (mn) / a.
Dit is dus de constructie van de vierde evenredige.
Deze constructie kan overigens worden gebaseerd op het gnomon-theorema.
Klik hier ![]() voor een animatie van de constructie volgens het gnomon-theorema.
voor een animatie van de constructie volgens het gnomon-theorema.
[einde Opmerking]
Terwijl het probleem van de parabolische aanpassing geheel bepaald is door het lijnstuk
a en de hoek j, is dat niet het geval voor de beide
andere aanpassingen. Hierbij eist Euclides nog een voorschift voor de vorm van het
parallelogram, dat uitsteekt of te kort schiet. Bij de hyperbolische aanpassing noemen we
dit het exces en bij de elliptische aanpassing het defect.
In Boek II treffen we alleen die vormen van aanpassing aan,
waarin het exces of het defect een vierkant is.
Opvallend is dat Euclides nergens in Boek II een constructie geeft voor het kwadratisch
exces of defect.
Toch kunnen we, zoals Simson in zijn boek The Elements of Euclid (Part 1) aannemelijk
heeft gemaakt, ervan uitgaan dat de Grieken toch op basis van de theorie in Boek II hebben
gewerkt.
Klik hier voor een uiteenzetting over de constructies van Simson.
3. Exces en
defect ![]()
De behandeling van de ellipische en hyperbolische aanpassing is opgedeeld
in de volgende paragrafen
3.1. Inleidende proposities
3.2. Defect
3.3. Oplossing van de vierkantsvergelijking ax - px2 = c2
3.4. Exces
3.5. Algebra?sche samenvatting
3.1. Inleidende proposities ![]()
Voordat Euclides verder ingaat op het exces en defect van de elliptische en hyperbolische
aanpassingen van een gegeven vorm, geeft hij eerste twee proposities die een aanvulling
zijn op het gnomon-theorema. We geven deze proposities zonder
verder bewijs.
Tussen beide proposities in, staat de belangrijke stelling die het fundament is van de
uitbreiding van de oppervlakterekening.
Overigens is niet duidelijk wat de reden hiervan is. Propositie 26 is immers onafhankelijk
van propositie 25 (dit is een constructie/existentiebewijs)
| Propositie VI-25 Eenzelfde [figuur] te construeeren, die gelijkvormig is met een gegeven rechtlijnige [figuur] en gelijk aan een andere gegeven rechtlijnige [figuur]. |
Zie figuur 1.
| figuur 1 | 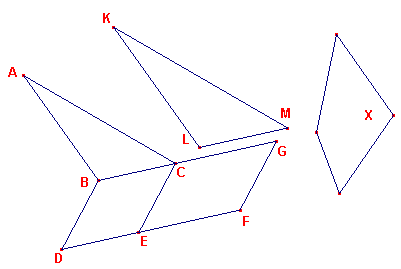 |
Zij ABC een driehoek waarmee de te construeren figuur gelijkvormig moet
zijn. Zij de oppervlakte van de teconstrueren figuur gelijk aan die van figuur X. We
construeren allereerst het parallelogram BE (op een willekeurige hoek) dat gelijk is aan
ABC. (volgens propositie I-44). Als nu LM de middenevenredige is tussen BC en CG, dan kunnen we KLM gelijkvormig construeren aan ABC. |
Klik hier ![]() voor een animatie
die het hierna volgende bewijs van de stelling illustreert.
voor een animatie
die het hierna volgende bewijs van de stelling illustreert.
Bewijs:
BC : LM = LM : CG
BC : CG = parallelogram(BE) : parallelogram(CF)
terwijl ook uit de redentheorie volgt
Maar (figuur op BC) : (figuur op LM) = BC : CG
(*)
Hieruit volgt dan, omdat (figuur op BC) = parallelogram(BE), dat ook (figuur op LM) =
parallelogram(CF) = X
(*) De Grieken beschouwden een evenredigheid niet als een getal.
Daardoor kan ook niet gesproken worden over kwadraten in algebra?sche zin.
We kunnen de genoemde eigenschap echter met onze moderne middelen eenvoudig afleiden.
ALS a : b = b : c
DAN a2 : b2 = a2 : ac
= a : c
De bedoelde eigenschap laat Euclides volgen uit (het hier niet opgenomen bewijs van)
propositie VI-19 die luidt
| Propositie VI-19 Gelijkvormige driehoeken staan tot elkaar in de dubbelreden van de overeenkomstige zijden |
Euclides formuleert het porisma (gevolg) van deze propositie als volgt
| Hieruit [uit het bewijs van de propositie; dk] is duidelijk, dat als drie lijnen evenredig zijn [a, b en c, als a : b = b : c; dk], dan als de eerste is tot de derde ook de figuur beschreven op de eerste evenredig is met de figuur die gelijkvormig beschreven is op de tweede. |
3.2. Defect ![]()
De elliptische aanpassing met een defect van voorgeschreven vorm wordt uitgevoerd in propositie VI-28.
Deze propositie wordt echter voorafgegaan door een propostie waarin een voorwaarde nodig
voor het uitvoeren van die constructie wordt geformuleerd.
Bewijs:
| figuur 2 | 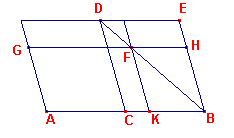 |
Zij AB de gegeven rechte (zie figuur 2), C het midden van AB en CBED
het parallelogram van de gegeven vorm op BC. Is nu F een willekeurig punt op BD, dan zegt de stelling dat P(AD) > P(AF). Nu heeft
het parallelogram AF (AKFG) een defect P(BF) dat gelijkvormig is met het parallelogram BD |
AF = CG +CF = CG + FE (dit figuren, geen lijnstukken!)
Ook is AD = CG + GD = CG + DH.
Omdat DH > FE is dus ook AD > AF. ?
Opmerking bij prop. VI-27
In moderne formulering vinden we, als we AB = a, BC / CD = p, FK = x
en hoek GAB = j stellen:
CD = ?a / p en oppervlakte(AKFG) = x. Uit de verhoudingen in driehoek
BCD vinden we dan, indien CK = y:
BK : BC = FK : CD of (?a - y)
: ?a = x : ?a / p. Waaruit
volgt dat y = ?a - px. Zodat AK = a - px.
De oppervlakte van AKFG is dus: x(a - px)sin j.
Het maximum van de uitdrukking ax - px2 vinden we nu voor x = a
/2p; het maximum is dus gelijk aan a2 / 4p. En dit komt
overeen met de oppervlakte van het parallelogram CBED.
[einde Opmerking]
Een afgeleide eigenschap van deze propositie is nu als voorwaarde opgenomen in
Zij AB de gegeven rechte met midden C. Zij X het gegeven oppervlak en Y de gegeven vorm van het defect (deze laatste staan niet in figuur 3).
| figuur 3 | 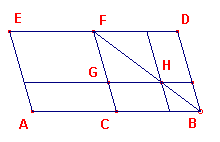 |
Euclides construeert eerst twee parallelogrammen ACFE en CBDF, ieder op
de helft van het lijnstuk AB en ieder gelijkvormig met Y. X mag dus niet groter zijn AF Als X = AF dan is AF de gevraagde figuur. Stel dus X < AF. Euclides geeft vervolgens aan, dat er een met Y gelijkvormig parallelogram geconstrueerd moet worden waarvan de oppervlakte gelijk is aan het verschil tussen AF en X. |
Deze constructie verloopt volgens propositie VI-25.
Dit parallelogram, FGHK, plaatst hij daarna in de hoek DFC van parallelogram BF.
Wegens propositieVI-26 ligt H op de diagonaal BF.
Nu is AH het gevraagde parallelogram.
Bewijs:
Nu is AH = AG + CH = BG + DH (geen lijnstukken! gnomon-theorema)
Dus is AH + FH = BG + DH + FH = BF,
terwijl ook X + FH = BF. Gevolg X = AH. ?
3.3. Oplossing van de vierkantsvergelijking ax - px2 = c2
![]()
Wanneer we ook nu weer het algebra?sche equivalent van deze constructie opschrijven, dan
volgt een verrassend resultaat.
We stellen AB = a, GC = x, BC / FC = p en X = c2.
Zonder afbreuk te doen aan de constructie gaan we ervan uit, dat Y een rechthoek is
Conform de Opmerking bij propositie VI-27 moet x nu voldoen
aan de vergelijking ax - px2 = c2
We kunnen nu schrijven
px2 - ax = - c2
We tellen bij beide leden nu a2/4p op om het linker lid tot een lineaire vorm in x te make. De meetlundige betekenis van a2/4p is de oppervlakte van parallelogram BF. In het rechter lid komt dan het verschil van BF en X te staan:
px2 - ax + a2/4p = a2/4p - c2
Deling door p geeft
(1) ..... x2 - a/p x + a2 / 4p2 = a2 / 4p2 - c2 / p of (x - a / 2p)2 = a2 / 4p2 - c2 / p
Om nu volgens propositie VI-25 het parallelogram FH te maken vervormen we dit verschil tot een parallelogram met basis a/2 en construeren de middenevenredige FG van de andere zijde die gelijk is aan (a2 / 4p - c2) / (a/2) en van a / 2p. We vinden dan
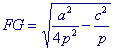 |
en omdat FG = a / 2p - x vinden we dus | 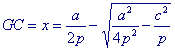 |
We zien dus dat we van bovenstaande vergelijking (1) slechts ??n wortel vinden
Alle stappen van de meetkundige constructie kunnen we dus in de algebra?sche oplossing terugvinden.
Ook de waarwaarde voor oplosbaarheid a2 / 4p ? c2 zien we (uiteraard) in de oplossing terug.
We missen bij Euclides de wortel x = a /2p +
?D. De meetkudnige betekenis hiervan is dat men het
parallelogram dat gelijk is aan het verschil van BF en X om het verlengde van BF
construeert.
Beide oplossingen van de vergelijking zijn dus in dit geval wel terug te vinden.
3.4. Exces ![]()
Geheel analoog aan propositie VI-28 wordt nu behandeld
Is AB weer de gegeven rechte met midden C en zij X het gegeven oppervlak en Y de gegeven vorm van het exces (deze laatste staan niet in figuur 4).
| Ook nu wordt in de hoek FEC een parallelogram EG beschreven dat gelijk is
aan de som van BE (het paralellelogram op het halve lijnstuk en X) en dat gelijkvormig is
met Y. Op dezelfde manier als in propositie VI-28 blijkt dan, dat
AG het gevraagde parallelogram is. ? Als we dezelfde notatie gebruiken als in paragraaf 3.3, dan is het algebra?sch equaivalent van deze constructie het oplossen van de vergelijking ax + px2 = c2 |
figuur 4 | 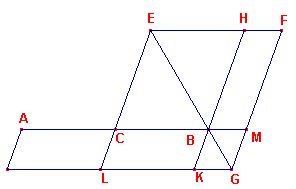 |
Ook hier kunnen we in de constructie weer alle stappen van de algebra?sche oplossing
terugvinden.
Ditmaal is het essentieel, dat Euclides slechts ??n oplossing kent. Immers de
vergelijking heeft nu ook een negatieve wortel. En dergelijke getallen hadden voor de
Grieken geen betekenis..
3.5. Algebra?sche samenvatting
![]()
Beide problemen, de elliptische en de hyperbolische aanpassing, bevatten de algemene
oplossing van het oplossen van een tweedegraads vergelijking.
Gaan we uit van de vergelijking
px2 ? ax ? c2 = 0
waarin p een positief (re?el) getal is en a en c de lengtes van lijnstukken voorstellen (dus ook positief), dan zijn positieve re?le oplossingen mogelijk in de volgende gevallen
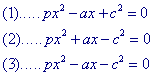
Geval (1) is identiek met het probleem in propositie VI-28. Het is
een elliptische aanpassing aan een lijunstuk met lengte a van een oppervlak ter
grootte van c2, met een defect in de vorm van een parallelogram met
zijdenverhouding p.
Geval (2) is identiek met het probleem in propositie VI-29. Het is een
hyperbolische aanpassing aan een lijnstuk met lengte a van een oppervlak, groot c2,
met een exces in de vorm van een parallelogram eveneens met een zijdenverhouding p.
Geval (3), dat we kunnen schrijven in de vorm px2 - ax = c2,
is blijkbaar eveneens een hyperbolische aanpassing aan een lijnstuk met lengte a.
Euclides behandelt dit geval niet. Het geval kan echter teruggebracht worden tot propositie VI-29.
Algebra?sch blijkt dit via de transformatie x = a/p + y,
waardoor de vergelijking overgaat in py2 + ay = c2.
En dit is geval (2).
| figuur 5 | 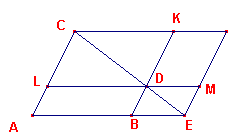 |
Meetkundig betekent de transformatie dat men bij een gegeven rechte AB = a
het parallelogram CE met zijdenverhouding p construeert, zodat het exces KE
gelijk is aan een gegeven oppervlak c2. Daarbij voert men BD als
nieuwe onbekende in: BD = KB - KD = x - a/p en vraagt dus naar het parallelogram AM dat gelijk is aan het gegeven oppervlak, en waarvan het exces BM de gegeven vorm heeft. |
Inderdaad is nu AM = AD + BM = KM + BM = KE.
Opmerking
Indien p = 1 kunnen de bijzondere gevallen van het tweedegraadsprobleem (in dit
geval hebben we een kwadratisch exces of defect) zonder gebruik te maken van de
redentheorie met behulp van de oppervlakterekening van Boek II
worden opgeslost.
[einde Opmerking]
4. Gulden
snede - uiterste en middelste reden ![]()
Als toepassing van de algemene oppervlakterekening wordt nu opnieuw het probleem uit Boek II, propositie 11 gesteld, echter nu geformuleerd in de
bewoordingen van de redentheorie.
Allereerst een definitie van de te gebruiken terminologie.
| Definitie VI-3 Men zegt dat een rechte in uiterste en middelste reden verdeeld is, wanneer, zoals het geheel tot het grootste stuk, zoo het grootste tot het kleinste staat |
en dan onmiddellijk gevolgd door
| Propositie VI-30 Een gegeven begrensde rechte in uiterste en middelste reden te verdelen |
Laat AB de gegeven begrensde rechte lijn zijn.
Ge?ist wordt AB in uiterste en middelste reden te verdelen
| figuur 6 | 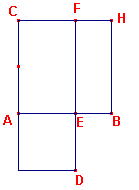 |
Laat op AB een vierkant beschreven zijn; en laat het parallelogram CD
aangepast zijn aan AC, gelijk aan BC en met een exces AD dat gelijkvormig is met BC
[volgens prop. VI-29]. Nu is BC een vierkant; daarom is ook AD
een vierkant. En, omdat BC gelijk is aan CD, laat CE van beide afgetrokken worden. Dus is de overblijvende [rechthoek] BF gelijk aan [het vierkant] AD. Maar deze zijn gelijkhoekig. Dus in BF, AD zijn de zijden rond de gelijke hoeken omgekeerd evenredig; dus zoals FE staat tot ED, is AE tot EB. Maar FE is gelijk aan AB, en ED [is gelijk] aan AE. Dus zoals BA staat tot AE, is AE tot EB. En AB is groter dan AE, dus is AE ook groter dan EB. |
Daarom is de rechte lijn AB in uiterste en middelste reden verdeeld door E, en het
grootste segment ervan is AE.
Hetgeen gedaan moest worden. ?
Opmerkingen
[1]
Bij de uitvoering van de aanpassing volgens VI-29 moet men op de helft van AC een
rechthoek constrieren die gelijk is aan de som van het vierkant op ?AC en het aan te
passen oppervlak AH. Is AB = a, dan wordt de tweede zijde van die rechthoek
gelijk aan 5/2a, immers a2 + 1/4a2 = 5/4a2
= 1/2a . 5/2a.
Volgens VI-25 moet men dan de middelevenredige (b) van 5/2a en 1/2a
nemen en deze over 1/2a heen afpassen. We vinden dan
b = ?(5/4a2) =
1/2a?5
en
ED = 1/2a?5 - 1/2a = 1/2a(?5 -1), een bekende uitdrukking!
Zie ook de Opmerking 3 bij propositie II-11.
[2]
Zie ook de pagina "Gulden snede en Getallen van Fibonacci".
[einde Opmerkingen]
5.
Uitgebreide Stelling van Pythagoras ![]()
In de volgende propositie vinden we de bekende uitbreiding van de stelling van Pythagoras (prop. I-47) bij het gebruik van
gelijkvormige veelhoeken op de zijden van een rechthoekige driehoek.
| Propositie VI-31 In rechthoekige driehoeken is een figuur, beschreven op de den rechten hoek onderspannende zijde, gelijk aan de op de den rechten hoek omvattende zijden op gelijke wijze beschreven gelijkvormige figuren |
Opmerkingen
[1]
Klik hier voor een commentaar van Proclus (411-485, Griekenland) bij Prop. I-47 en
Prop. VI-31.
[2]
Klik hier voor het bewijs van Prop. VI-13 met de
vertaalde tekst uit de Elementen (hieronder staat het bewijs in een "moderne"
vorm).
[einde Opmerkingen]
In figuur 7 is AD loodrecht op BC. Nu is CB : BA = BA : BD.
| figuur 7 | 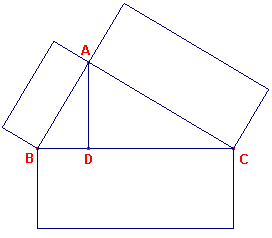 |
En hieruit volgt weer (zie de opmerking bij
prop. VI-19) CB : BD = opp(BC) : opp(AB), waarin opp(PQ) betekent: de oppervlakte van de figuur beschreven op het lijnstuk PQ. Evenzo: CB : CD = opp(BC) : opp(AC) waaruit we kunnen afleiden, dat BD : opp(AB) = CD : opp(AC), of BD : CD = opp(AB) : opp(AC). Hieruit volgt dan het gestelde, omdat BD + CD = BC ? |
Klik hier ![]() voor een animatie
van deze stelling.
voor een animatie
van deze stelling.
[3]
Een toepassing van Prop. VI-31 is te vinden op de pagina "Maantjes van Hippocrates".