Defect en Exces

Kwadratisch defect en exces volgens Simson

Inleiding | Defect | Exces ][ Boek VI | Elementen

1. Inleiding
In Boek II komen geen constructies voor die betrekking hebben op het kwadratisch defect en exces van niet-parabolische aanpassingen van oppervlakken.
Door Simson is in zijn boek The Elements of Euclid (Part 1) aangeven hoe de Grieken vermoedelijk te werk zijn gegaan.
Daarvoor zijn eigenlijk alleen propositie 5 en propositie 6 uit Boek II van de Elementen noodzakelijk.
Als referentie laten we deze hieronder volgen.

Propositie II-5
Indien een rechte lijn verdeeld wordt in gelijke en ongelijke deelem, is de rechthoek, omvat door de ongelijke deelen van het geheel, samen met het vierkant op het stuk tusschen de deelpunten, gelijk aan het vierkant op de helft.
Propositie II-6
Indien een rechte lijn middendoor wordt gedeeld en er wordt een rechte in rechte lijn aan haar toegevoegd, dan is de rechthoek, omvat door de heele rechte met de toegevoegde en de toegevoegde samen met het vierkant op de helft, gelijk aan het vierkant op de rechte, bestaande uit de helft en de toegevoegde.

2. Defect
Zij AB een lijnstuk en zij X een oppervlak dat conform propositie II-14 equivalent getransformeerd is in een vierkant V(p); p is dus de lengte van de zijde van een vierkant.
De vraag is nu op het lijnstuk AB een punt T te construeren, zodat

R(AT, BT) = V(p)

Zie nu figuur 1.

figuur 1

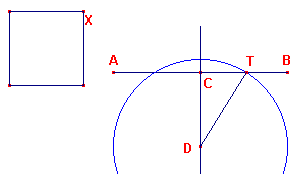Kies C als midden van AB en trek CD loodrecht in C op AB.
Maak dan CD gelijk aan p.
Beschrijf vervolgens de cirkel (C, BC).
Een snijpunt T van deze cirkel met AB is dan het gevraagde punt.

Bewijs:
Volgens propositie II-5 is nu
R(AT, TB) + V(CT) = V(BC)
Volgens propositie II-47 (stelling van Pythagoras) is verder

V(p) + V(CT) = V(TD) = V(BC), immers TD = BC. Uit beide volgt dan onmiddellijk, dat R(AT, TB) = V(p) ?

Een nodige en voldoende voorwaarde voor de uitvoerbaarheid van de constructie is, dat p ? BC of V(p) ? V(BC).
Euclides vermeldt deze voorwaarde in propositie VI-27 die voorafgaat aan de algemene behandeling van de elliptische aanpassing in propositie VI-28.

Stellen we nu AB = a, AT = x en p = b, dan is het moderne equivalent van het kwadratisch defect blijkbaar de oplossing van de vierkantsvergelijking

x (a - x) = b² of
ax - x² = b² (met a>0)

De meetkundige voorwaarde voor uitvoering van de constructie, V(p) ? V(BC), luidt in algebra?sche vorm: b² ? a² / 4.

Opmerking
Stellen we AT = x en BT = y, dan zijn x en y dus blijkbaar de oplossingen van het stelsel vergelijkingen
x + y = a, xy = b²[einde opmerking]

3. Exces
Voor het vinden van het exces moeten we op het verlengde van AB een punt T vinden zodat

R(AT, BT) = V(p)

Zie nu figuur 2.

figuur 2

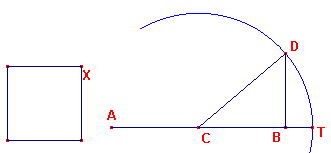Kies opnieuw het punt C als midden van AB. Trek BD in B loodrecht op AB en maak BD = p.
Beschrijf vervolgens de cirkel (C, CD).
Het snijpunt van deze cirkel met het verlengde van AB is adan het gevraagde punt T.

Bewijs:
Volgens propositie II-6 is dan
R(AT, BT) + V(BC) = V(CT).

Volgens propositie I-47 (stelling van Pythagoras) is nu V(p) + V(BC) = V(CD) = V(CT).

Uit beide volgt nu onmiddellijk dat R(AT, BT) = V(CT) ?

Stellen we nu AT = a en BT = x, dan is het algebra?sch equivalent van de hyperbolische aanpassing met kwadratisch exces dus de bepaling van de positieve wortel van de de vierkantsvergelijking

(a + x) x = b² of
ax + x² = b²

Opmerkingen
[1]
Stellen we echter AT = x en BT = y, dan komt de vraag dus neer op het bepalen van positieve getallen x en y die voldoen aan het stelstel vergelijkingen
x + y = a, xy = b²

[2]
De verdeling van een lijnstuk is middelste en uiterste reden kan worden opgevat als een bijzondere vorm van de hyperbolische aanpassing met kwadratisch exces, namelijk die, waarin het aan te passen oppervlak gelijk is aan het vierkant op het gegeven lijnstuk AB.
We bekijken daartoe de figuur die geplaatst is bij propositie II-11, en waarin de constructie is weergegeven van het punt T dat het lijnstuk AB verdeelt in middelste en uiterste reden via de constructie van het punt Z op het verlengde van CA (zie hiervoor ook de animatie die behoort bij propositie II-11).

figuur 3

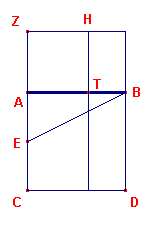In deze figuur (zie figuur 3) is het punt Z geconstrueerd bij de hyperbolische aanpassing op het lijnstuk AC (dat gelijk is aan AB).
Het punt Z wordt gevonden door EZ (waarbij E het midden is van AC) op het verlengde van CA te kiezen, en wel zo, dat EZ = EB.

De constructie van het punt Z (door Euclides) komt dus geheel overeen met die welke Simson heeft gegeven voor het meer algemene geval van de hyperbolische aanpassing (zie het begin van paragraaf 3).

[einde Opmerkingen]

Vorige pagina Top

[propVIsims.htm] laatste wijziging op: 22-10-1999