Hyperbolische meetkunde [3]: Congruentie
Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde
1. Gelijkheid van lijnstukken
We defini�ren:
| Definities (P-meetkunde) [1] Zij AB en CD twee gegeven d-lijnstukken. Als er een H-afbeelding F is, met F(A) = C �n F(B) = D, dan is AB = CD (impliciet: de afstand van A tot B is gelijk aan de afstand van C tot D). We noteren ook wel AB (d)= CD. [2] Het punt M heet midden van het lijnstuk AB indien AM = MB. |
Opmerking
In deze definitie is niet het begrip "afstand" zelf vastgelegd.
[einde Opmerking]
| Stelling 1 Voor ieder lijnstuk AB geldt: AB (d)=BA |
Bewijs:
Er is een H-afbeelding F, met F(A) = B en F(B) = A (zie de pagina "H-Meetkunde[1]").
Hieruit volgt onmiddellijk het gestelde. �
| Definities [1] Een d-driehoek is een figuur die bestaat uit drie (niet op dezelfde d-lijn gelegen) d-punten en de d-lijnstukken die de punten verbinden. [2] Twee d-driehoeken ABC en A'B'C' zijn d-congruent (notatie ABC (d)= A'B'C') als er een H-afbeelding F is met F(A)=A', F(B)=B' en F(C)=C'. |
We bewijzen nu een stelling die we ook in de E-meetkunde kennen. Ook de overeenkomstige niet-genoemde stellingen over congruentie van d-driehoeken kunnen op dezelfde manier bewezen worden.
| Stelling 2 Twee d-driehoeken ABC en A'B'C' zijn d-congruent indien geldt: hoek CAB = hoek C'A'B', AB = A'B' en AC = A'C' (geval ZHZ). |
Bewijs:
| figuur 1 | 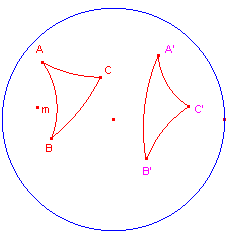 |
We gaan er eerst van uit, dat ABC en A'B'C' dezelfde ori�ntatie
hebben (zie figuur 1). Uit AB = A'B' volgt, dat er een unieke H-afbeelding F is met F(A)=A' en F(B)=B'. F is een conforme afbeelding. Daardoor wordt de gelijke hoek A afgebeeld op de hoek A'. Hierdoor wordt AC afgebeeld op de drager van A'C' en wegens AC=A'C' vinden we dus F(C)=C'. Als de driehoeken verschillende ori�ntatie hebben, dan beelden we A'B'C' af op het E-meetkundige beeld A"B"C" onder de spiegeling in een middellijn van de horizon (zie Opmerking). ABC en A"B"C" hebben nu dezelfde orientatie en zijn dus d-congruent. Waaruit weer volgt, dat ook ABC (d)=A'B'C'.� |
Opmerking
We hebben in bovenstaand bewijs een afbeelding gebruikt die tot nu toe niet was
toegestaan, nl. de spiegeling in een middellijn van de horizon. De spiegeling is namelijk
geen H-afbeelding.
Bij de spiegeling in een middellijn van de horizon worden echter wel de disk en de horizon
op zichzelf afgebeeld.
We breiden de verzameling H uit met de spiegeling in de x-as (of alle spiegelingen in een
middellijn van de horizon).
Hierdoor wordt het werken met figuren met een tegengestelde ori�ntatie mogelijk.
We kunnen zouden het ook wel zonder deze toevoeging kunnen doen, maar dan moeten we het congruentiegeval ZHZ (of een ander congruentiegeval) als axioma
voor de hyperbolische meetkunde opnemen.
[einde Opmerking]
| Stelling 3 Als in een d-driehoek ABC geldt dat AB=AC (ABC is een gelijkbenige driehoek), dan is hoek B = hoek C. |
Klik hier ![]() voor een animatie
van deze stelling (waarin een schets van een tweede bewijs).
voor een animatie
van deze stelling (waarin een schets van een tweede bewijs).
Bewijs:
We bekijken driehoek CAB en BAC. Deze (verschillende!) driehoeken zijn congruent (ZHZ).
Dus is hoek B = hoek C.�
Een gevolg van deze stelling is
| Stelling 4 In een d-driehoek ligt tegenover de grootste zijde de grootste hoek. |
| figuur 2 | 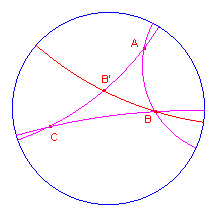 |
Bewijs: (zie figuur 2) Stel dat AC de grootste zijde is. Dan is dus AC>AB. Kies nu op de zijde AC een punt B', zodat AB'=AB. Dan is ABB' een gelijkbenige driehoek. Dus hoek ABB' = hoek AB'B. BB' ligt binnen driehoek ABC, zodat hoek ABC>hoekAB'B. Maar AB'B is een buitenhoek van driehoek B'CB. Zodat hoek AB'B > hoek C. We hebben dus hoek B > hoek C. Op dezelfde manier bewijzen we, dat hoek B > hoek A.� |
3. "Gelijkvormige driehoeken"
We hebben op deze pagina een drietal stellingen uit de P-meetkunde gezien die in de
E-meetkunde op dezelfde wijze geformuleerd worden. De oorzaak daarvan is gelegen in het
feit, dat deze stellingen onafhankelijk zijn van het 5e postulaat
(parallellen-postulaat).
We kunnen de eerste 28 proposities uit de Elementen van
Euclides dus ook bewijzen in de P-meetkunde.
Een belangrijk verschil tussen de P- en E-meetkunde is de hoekensom.
Maar ook gelijkvormige driehoeken (driehoeken waarvan de overeenkomstige
hoeken gelijk zijn) wijken af van wat we in de E-meetkunde gewend zijn.
| Stelling 5 (P-meetkunde) Gelijkvormige d-driehoeken zijn congruent. |
Klik hier ![]() voor een animatie
van stelling 5.
voor een animatie
van stelling 5.
| figuur 3 | 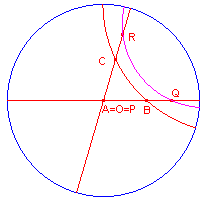 |
Bewijs: We gaan uit van de driehoeken ABC en PQR waarin de paren overeenkomstige hoeken, (A,P, (B,Q), (C,R) gelijk zijn. We passen nu een H-afbeelding toe op driehoek ABC, waardoor A samenvalt met O. We passen op P een H-afbeelding toe waardoor P eveneens samenvalt met O. Door een rotatie om O kunnen we, omdat hoek A gelijk is aan hoek P, ervoor zorgen Q op B en R op AC ligt. Zie nu figuur 3, waarvan we zullen bewijzen, dat R=C en Q=B. De verschillende onmogelijke liggingen van R en Q zijn weergegeven in figuur 4, waarbij we, voor de eenvoud van de illustratie, Euclidische lijnen heben getekend |
| . |
| figuur 4 | 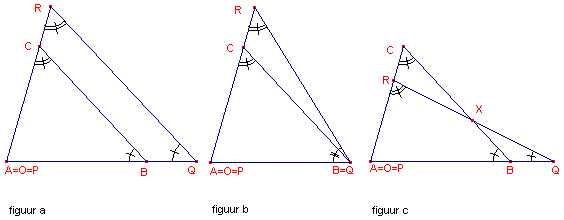 |
(a) hoek RCB = 180� - hoek C; hoek CBQ = 180� - hoek B
De hoekensom van vierhoek BQRC is dus gelijk aan: (180� - hoek B)+hoek Q+hoek R+(180� -
hoek C)=360�, hetgeen onmogelijk is omdat de som van de hoeken van een d-vierhoek kleiner
is dan 180�.
(b) hoek RCB = 180� - hoek C.
De hoekensom van d-driehoek RCB is gelijk aan: hoek R + 180� - hoek C + hoek B >
180�. Dit onmogelijk, omdat de hoekensom van een d-driehoek kleiner is dan 180�.
(c) In d-driehoek XBQ is nu de hoekensom gelijk aan: hoek BXQ + (180� - hoek B) + hoek
BQX > 180�. Eveneens onmogelijk.
De enige ligging die mogelijk is, is het samenvallen van R met C en Q met B.
De beide d-driehoeken zijn dus congruent.�
[hypm3.htm] laatste wijziging op: 03-06-2000