Harmonikaal / pool en poollijn bij een driehoek

Overzicht  ][  Vierzijde | Stralenbundels | Meetkunde

Overzicht terug

  1. Inleiding cabrisignal.gif (160 bytes)
  2. Hoogtepunt en harmonikaal
  3. Lemoine-lijn

1. Inleiding terug

Stelling 1
De vierde harmonische punten elk bij het snijpunt van drie in P concurrente hoektransversalen met een zijde en de beide hoekpunten op die zijde zijn collineair op een lijn p.

Bewijs:

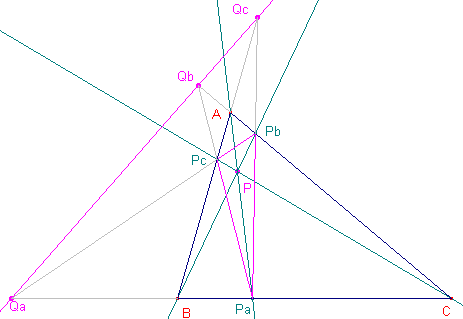harmon1.gif (6056 bytes) In driehoek ABC zijn PA, PB, PC hoektransversale, Pa, Pb, Pc de snijpunten ervan met de zijden.
Qc, Qa, Qb zijn de 4e harmonische punten bij opvolgend ABPc, BCPa, ABPc.
Uit de constructie voor harmonische punten (zie pagina de pagina "Stralenbundels", Stelling 3 en paragraaf 2 Constructies daarop) volgt onmiddellijk dat Qa = PbPc /\ BC, enz.
De driehoeken ABC en PaPbPc zijn perspectief in P.
Volgens de stelling van Desargues zijn dan de punten Qa, Qb, Qc collineair. �

Op basis van Stelling 1 geven we nu de volgende:

Definitie
Het punt P heet pool (harmonikaalpunt) van de lijn p tov. de driehoek.
De lijn p heet harmonikaal (poollijn) van P tov. de driehoek.

Klik hier >Applet< voor een CabriJavapplet bij Stelling 1.

Gevolgen

harmon2.gif (3793 bytes) [1]
P is het incentrum van driehoek ABC.
De snijpunten van de buitenbissectrices snijden de overstaande zijden in drie collineaire punten.
harmon3.gif (4695 bytes) [2]
P is het hoogtepunt van de driehoek.
De zijden van de hoogtepuntsdriehoek snijdende overeenkomstige zijden van de driehoek in collineaire punten.

Zie verder paragraaf 2.
harmon4.gif (3888 bytes) [3]
P is het zwaartepunt van de driehoek
De harmonikaal van Z is de oneigenlijke rechte.

2. Hoogtepunt en harmonikaal terug

Stelling 2
[1]
De harmonikaal h van het hoogtepunt H is de machtlijn van de negenpuntscirkel en de omcirkel van een driehoek.
[2]
h staat loodrecht op de Euler-lijn van de driehoek.

Bewijs: (met een iets andere belettering als in Gevolg 2 hierboven)

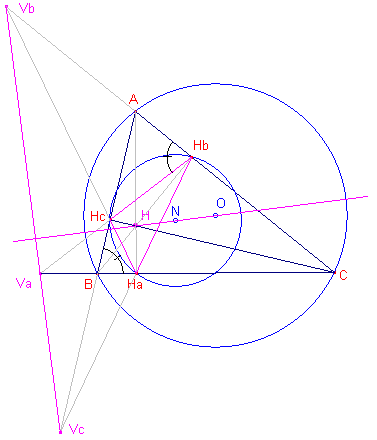harmon5.gif (6994 bytes) [1]
Volgens een bekende eigenschap is:
AHbB = B, zodat
BHbVa = 90� - B.
In driehoek BCHc is BCHc = VaCHc= 90� - B
De driehoeken BHbVa en CHcVa hebben naast bovengenoemde hoeken ook hoek Va gelijk. Dus:
BHbVa ~ HcCVa
We vinden daaruit:
VaB : VaHc = VaHb : VaC
of
VaB � VaC = VaHc � VaHb
Nu is
VaB � VaC = de macht van Va tov. de omcirkel, en
VaHc � VaHb =  de macht van Va tov. negenpuntscirkel.
Va heeft dus gelijke machten tov. de omcirkel en negenpuntscirkel.
Analoog kan dit bewezen worden voor Vb en Vc.
VaVbVc is dus de machtlijn van de omcirkel en de negenpuntscirkel.

[2]
ON, de Euler-lijn van de driehoek, is de centraal van beide cirkels.
Volgens Stelling 5 op de pagina "De macht van een punt..." staat de machtlijn van twee cirkels loodrecht op hun centraal. �

3. Lemoine-lijn terug

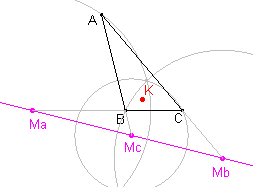
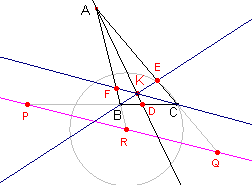
harmonp31.gif (3381 bytes)        harmonp32.gif (3624 bytes) Oa. op de pagina "Isodynamische punten" is de Lemoine-lijn behandeld als de collineatie-as van de middelpunten van de Apollonius-cirkels van een driehoek; zie hiernaast, de linker figuur.

In de rechter figuur is de lijn PQR de harmonikaal van het Lemoine-punt K.

Er geldt nu:
Stelling 3
De Lemoine-lijn is de harmonikaal van het Lemoine-punt tov. de driehoek.

newy.gif (116 bytes)Bewijs:
Het bewijs is opgenomen in een PDF-bestand over involuties (Involuties: algebra�sch en meetkundig).
Klik hier om dat bestand te downloaden (p: involutie.pdf; ca. 139 kB).

Een PDF-bestand kan gelezen worden met Adobe� Reader (vroeger Acrobat� Reader) : getacro.gif (1425 bytes)

begin pagina
[harmonikaal.htm] laatste wijziging op: 19-07-05