Stralenbundels

Stralenbundels

Overzicht ][ Vierzijde | Transversalen | DK & Meetkunde

Overzicht

Definities en stellingen
Constructies
Harmonische vierhoek

1. Definities en stellingen

figuur 1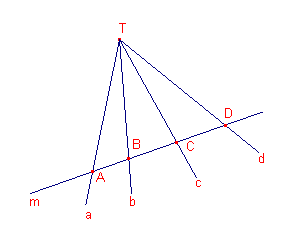

Definities
[1] Een stralenbundel (ook wel lijnenbundel genoemd) is een verzameling lijnen (niet noodzakelijk oneindig veel) die door ��n punt gaan.
De lijnen worden ook wel stralen genoemd. Het punt heet de top van de stralenbundel.
[2] Een stralenbundel bestaande uit vier stralen heet vierstraal.
[3] Een transversaal van een stralenbundel is een lijn die niet door de top van de stralenbundel gaat en alle lijnen van de bundel snijdt.
[4] Onder de dubbelverhouding T(abcd) van vier lijnen a, b, c, d in een stralenbundel (met top T) verstaan we de dubbelverhouding (ABCD) waarbij A,B,C,D de snijpunten zijn van opvolgend a,b,c,d met een transversaal van de bundel.
Dus: T(abcd) = (ABCD).
[5] Een vierstraal a,b,c,d met T(abcd) = -1 heet harmonische vierstraal.
De harmonische vierstraal wordt ook zelf wel aangegeven met T(abcd) of met T(ABCD).

Stelling 1
T(ABCD) is een vierstraal.
Voorts is l de lijn door B evenwijdig met de toegevoegde straal (de straal door A). l snijdt de beide andere stralen in de punten P en Q.
T(ABCD) = -1 desda PB= BQ

Bewijs:
Zie figuur 2.

figuur 2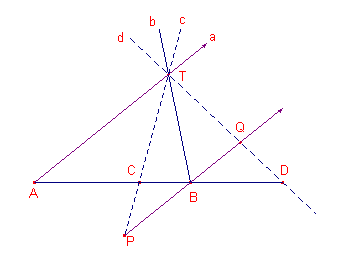

Als T(ABCD) = -1, dan is (volgens de definitie) ook (ABCD) = -1.
Stel dan AC = a en BC = b. Dus is AD = ka en BD = kb.
   BQ : TA = kb : ka = b : a
   BP : TA = b : a
Waaruit volgt dat BP = BQ.
Omgekeerd.
Zij BP = BQ.
Nu is BP : TA = BC : AC = b : a.
Dus, wegens BP = BQ, hebben we BQ : TA = b : a, dus ook BD : DA = b : a
Hieruit volgt dan BD = kb en DA = ka, zodat
   (ABCD) = CA/CB : DA/DB = (-b/a) : (kb/ka) = -1. �

Stelling 2
Twee snijdende rechten a, b worden door de bissectrices c, d van de hoeken die ze met elkaar maken, harmonisch gescheiden.

Bewijs:

figuur 3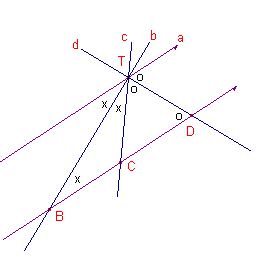

Zie figuur 3.

Trek de lijn l evenwijdig met a.
l snijdt b, c, d opvolgend in B, C, D.
In driehoek CTB is hoek C = hoek C; in driehoek CDT is hoek D = hoek T.
Beide driehoeken zijn dus gelijkbenig, zodat CB = CT = CD.
Volgens stelling 1 is dus T(abcd) = -1. �

Gevolg
Als van de harmonische vierstraal T(abcd) de stralen c en d loodrecht op elkaar staan, dan delen ze de hoeken tussen a en b middendoor.
[einde Gevolg]

Stelling 3
Twee diagonalen van een volledige vierzijde scheiden de hoekpunten op de derde diagonaal harmonisch.

Bewijs: (zie figuur 4)

figuur 4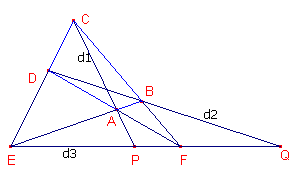

ABCDEF is de volledige vierzijde (AB,BC,CD, DA).
AC en BD zijn opvolgend de 1e en de 2e diagonaal. EF is de 3e diagonaal.
Te bewijzen is nu dat (EFPQ) = -1.

In driehoek CEF passen we de stelling van Menelaos toe op de transversaal DBQ.
Nu is (CED)(EFQ)(FCB) = 1.
Door A gaan drie hoektransversalen in dezelfde driehoek.
Volgens de stelling van Ceva is dan
(CED)(EFP)(FCB)= -1.

Dus, na deling van beide resultaten: (EFP)/(EFQ) = -1 of PE/FE : QE/QF = (EFPQ) = -1. �

Opmerking
Zie verder ook de pagina "Harmonikaal".
[einde Opmerking]

2. Constructies
Op basis van stelling 1 en stelling 3 in paragraaf 1 kunnen we nu een tweetal verschillende constructies geven voor de vierde harmonische bij drie gegeven collineaire punten.

1e Constructie

figuur 5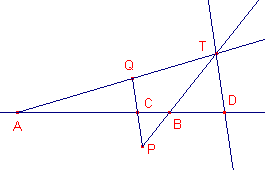

Zie figuur 5.

Gegeven zijn de punten A, B, C, met C tussen A en B (dus op het lijnstuk AB).
(1) Kies het lijnstuk PQ door C met PC = QC.
(2) Trek AQ.
(3) Trek BP; bepaal het snijpunt T van AQ en PB.
(4) Trek TD evenwijdig met PQ (D op de lijn AB).

Klik hier voor een stapsgewijze animatie van deze constructie.

Opmerkingen
[1] Voor het bewijs van deze constructie zie stelling 1.
[2] Bij deze constructie moet gebruik gemaakt worden van passer en liniaal.
[einde Opmerkingen]

2e constructie

figuur 6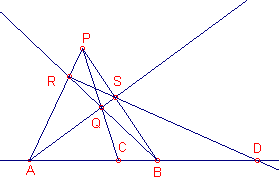

Zie figuur 6.

Gegeven de punten A, B, C met C tussen A en B.
(1) Kies punt P buiten de lijn AB.
(2) Trek PA, PB, PC.
(3) Kies Q op PC.
(4) Trek BQ en bepaal R op PA.
(5) Trek AQ en bepaal S op PB.
(6) Trek RS en bepaal D op AB.

Klik hier voor een stapsgewijze animatie van deze constructie.

Opmerkingen
[1] Voor het bewijs van deze constructie zie stelling 3.
[2] Bij deze constructie is alleen gebruik gemaakt van een liniaal.
[einde Opmerkingen]

3. Harmonische vierhoek

Definitie
Een harmonische vierhoek is een koordenvierhoek waarvan de producten van de overstaande zijden gelijk zijn.

Stelling 4
Een harmonische vierstraal T(abcd) waarvan T op een cirkel ligt, bepaalt op die cirkel een harmonische vierhoek ABCD, waarbij A, B, C, D de snijpunten zijn van de stralen met de cirkel).

Bewijs:

figuur 7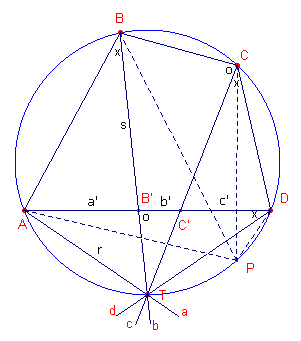

Zie figuur 7.

We kiezen de lijn door A en D als transversaal van de vierstraal. De lijnen b en c snijden AD in B’ en C’.
Nu is A, C’, B’, D een harmonisch viertal.
Voor een willekeurig punt P van de cirkel hebben we nu
P(a’b’c’d’) = T(abcd) = -1.
De beide vierstralen zijn dus congruent. We doen dus de algemeenheid niet te kort door de vierstraal zo te kiezen, dat T op de middelloodlijn van AD ligt.

De lengten van de zijden van vierhoek ABCD geven we (mogelijk wat verwarrend) ook aan met a, b, c, d.
Zij AB’ = a’, B’C’ = b’, C’D = c’, TA = TB = r, TB = s
Nu is
TAB’ ~ TBA, immers hoek A in TAB’ is gelijk aan hoek B in TBA (staande op dezelfde boog) en hoek T is gemeenschappelijk.
Dus: AB’ : BA = TA : TB en dus a’ : a = r : s.

Om dezelfde reden hebben we
TDC’ ~ TCD, waaruit volgt:
   DC’ : CD = TC’ : TD, zodat c’ : c = TC’ : r
Door vermenigvuldiging volgt uit deze laatste resultaten, dat a’c’ : ac = TC’ : r.
Duidelijk is dat TB’C’ ~ TCB, zodat B’C’ : CB = TC’ : TB, waaruit b’ : b = TC’ : s.
Combinatie hiervan met het vorige resultaat geeft:
   a’c’ : ac = b’ : b = b’d : bd.
Uit (AC’B’D) = B’A/B’C’ : DA/DC’ = -a’ / b’ : (-d) / (-c’) = -1, vinden we a’c’ = b’d.
Dit samen met het vorige resultaat geeft
   ac = bd.
De producten van de overstaande zijden zijn gelijk. Dus is ABCD een harmonische vierhoek. �

Opmerking
Volgens de stelling van Ptolemaeus is dus ac = bd = � pq, waarbij p en q de lengtes zijn van de diagonalen van de koordenvierhoek.
[einde Opmerking]

[stralenb.htm] laatste wijziging op: 02-03-2004