Ellipsograaf  |  Constructie  |  Bewijs  ][  Kegelsneden  |  Macro's voor kegelsneden  |  Cabri

Vorige Begin

figuur 8a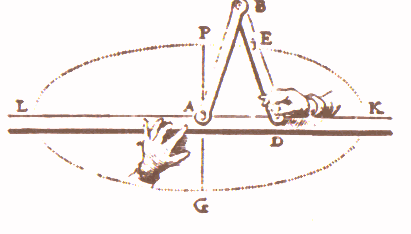

figuur 8b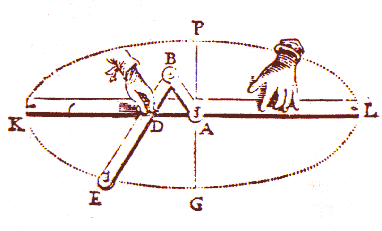

Twee stangen zijn in het punt B scharnierend aan elkaar verbonden. In het punt E is een schrijfstift bevestigd.
Het eindpunt A van de ene stang is scharnierend bevestigd in de oorsprong. Het punt D van de andere stang kan alleen horizontaal worden bewogen langs een lat KL..
In het "Museo Universitario di Storia Naturale e della Strumentazione Scientifica" te Modena (Itali�) bevindt zich ook een dergelijk apparaat (zie figuur 9).

figuur 9

Constructie
We kunnen in Cabri een model van deze ellipsograaf maken.
In figuur 8a kan het punt D op KL precies de lengte van AB+BD afleggen.
De maximale lengte van KL is dus 4 ^. AB.

• Teken een lijnstuk, waarvan de lengte a gelijk is aan de lengte van AB.
• Teken een lijnstuk KL waarvan de lengte 4a is.
• Teken het punt A als midden van KL.
• Kies het punt D op KL (met de functie "Punt op object" in het Punt-menu).
• Teken de cirkels (A, a) en (D, a).
• Zij B ��n van de snijpunten van deze cirkels.
• Kies het punt E op BD.
• Construeer het spiegelbeeld van E’ van E in de lijn KL.

figuur 10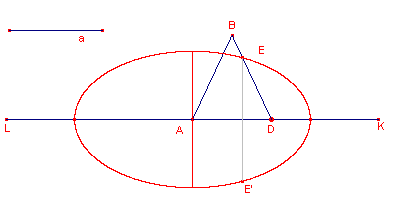

De ellips wordt nu bepaald door de punten E en E’, als het punt D het lijnstuk KL doorloopt.
Nb.
Cabri tekent ook een lijnstuk door A loodrecht op de lijn KL.

Klik hier voor een animatie bij deze constructie.

Bewijs
Ook nu is een bewijs op zijn plaats.
Stel de co�rdinaten van het punt D (op de lijn KL) zijn (2d,0).
Stel X ligt op BD, zodat DA=ka (zie figuur 11):

figuur 11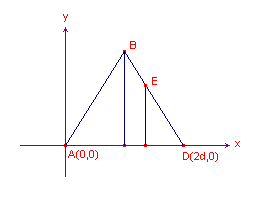

Voor de co�rdinaten van het punt B hebben we dan:

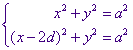
Hieruit volgt dan .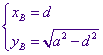

Voor het punt E volgt hieruit, vanwege de verhouding k : 1 op het lijnstuk DB:

(8.1) ... 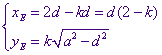waaruit dus volgt: .

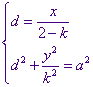Eliminatie van d uit deze laatste betrekkingen levert dan de vergelijking van de ellips:

   of .

Opmerkingen
[1]
Voor k = 1 (het punt E valt dan samen met B) gaat deze vergelijking in:
   
Dit is de vergelijking van de cirkel met middelpunt A en straal a.
[2]
Voor k = 2 is de betrekking niet gedefinieerd.
In dit geval geldt 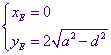; zie betrekking (8.1).
De meetkundige plaats van de punten E is in dit geval dus de y-as.
[einde Opmerkingen]

Vorige Begin

[ellips8.htm] laatste wijziging op: 08-06-2000