[ Alle Vragen | Meetkunde | Cabri ]
Vraag 9
Hoe is het begrip "oneindig" in Cabri ge�mplementeerd? ![]()
Toepassing 1 | Toepassing 2
Antwoord
Opmerking
Voor onderstaande toepassingen is het noodzakelijk, dat de Optie (in Voorkeuren |
Meetkunde) "Objecten in het oneindige" Aan staat.
Zie ook het antwoord op Vraag 21.
[einde Opmerking]
Binnen Cabri is het (tot op zekere hoogte) mogelijk dit begrip te hanteren. Het beste
laat het zich illustreren aan het "snijpunt" van twee evenwijdige lijnen.
Zoals bekend (zie ook het Cabri-werkblad "Co�rdinaten
in Cabri") worden alle figuren in Cabri vastgelegd ten opzichte van een
(onzichtbaar, maar zichtbaar te maken) orthonormaal assenstelsel.
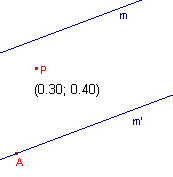
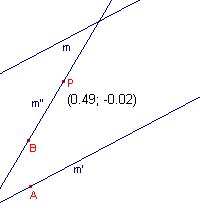
We gaan uit van een rechte lijn m en een punt P daarbuiten (zie de linker figuur
hieronder).
Door een punt A buiten die lijn is een lijn m' getekend evenwijdig met m.
Van het punt P zijn de co�rdinaten zichtbaar gemaakt.
| fig. a | fig. b | fig.c | ||
 |
 |
 |
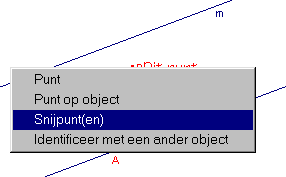
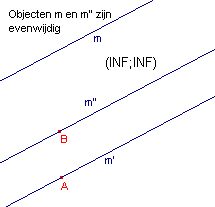
1 - Kies nu de functie "Herdefinieer object" in het Constructie-menu.
Hiermee kunnen we het punt P (opnieuw) defini�ren, maar nu als "snijpunt" van
de lijnen m en m':
2 - Selecteer het punt P
3 - Activeer de optie Snijpunt(en); zie middelste figuur
4 - Selecteer nu de lijnen m en m'.
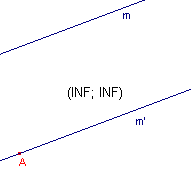
Hierna veranderen de co�rdinaten van P in (INF; INF); zie de rechter figuur.
P valt nu samen met het oneigenlijke punt van de lijnen m en m'.
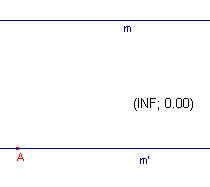 |
Opmerking Als de lijn m evenwijdig is met de x-as of de y-as, dan is de tweede cq. de eerste co�rdinaat gelijk aan 0; zie figuur hiernaast. [einde Opmerking] |
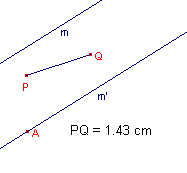
Kiezen we door het punt B (en ook door P) een lijn m" die de lijn m
snijdt (zie de linker figuur hieronder), dan kunnen we hetzelfde doen: P opnieuw
defini�ren als snijpunt van de lijnen m en m'.
Met Cabri kan onderzocht worden (via het Eigenschappen-menu) wat er in dit geval
aan de hand is met de lijn m" ten opzichte van de lijn m (zie
rechter figuur)).
 |
 |
In de volgende figuren is ge�llustreerd wat er met de afstand tussen de punten P en Q gebeurt, als het punt P opnieuw gedefinieerd wordt als snijpunt van de evenwijdige lijnen m en m'.
 |
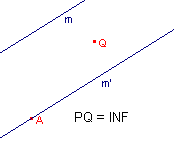 |
Nu is: PQ = INF |
Toepassing 9.1 ![]()
We kunnen een rechte lijn opvatten als een cirkel waarvan het middelpunt op de
oneigenlijke rechte ligt.
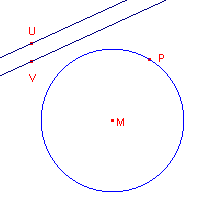
In onderstaande figuur (links) staat een cirkel die door het (onafhankelijke) punt P gaat
Het middelpunt M van die cirkel laten we samenvallen met het oneigenlijke punt bepaald
door de twee evenwijdige lijnen door U en V.
 |
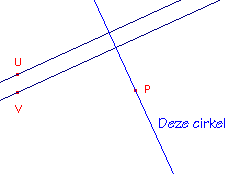 |
Na "verplaatsing" (herdefini�ring) van M zien we een
"rechte lijn" door P die loodrecht staat op de richting van de lijnen door U en
V. De lijn wordt door Cabri nog steeds gezien als een cirkel (zie de tekst Deze cirkel). |
Toepassing 9.2 ![]()
We kunnen met Cabri nu eenvoudig laten zien, dat raaklijnen uit een oneigenlijk
punt aan een cirkel evenwijdig zijn.
Klik hier voor deze illustratie.
[faq9.htm] laatst wwijziging op: 09-07-01