Cabri-FAQ (10)

[ Alle Vragen | Meetkunde | Cabri ]

Vorige

Begin

Volgende

Vraag 10
Hoe vind ik de oneigenlijke rechte (lijn op oneindig)?
Toepassing 1 | Toepassing 2 | Toepassing 3

Antwoord

Opmerking
Voor onderstaande toepassingen is het noodzakelijk, dat de Optie (in Voorkeuren | Meetkunde) "Objecten in het oneindige" Aan staat.
Zie ook het antwoord op Vraag 21.
[einde Opmerking]

In het antwoord op Vraag 9 kunnen we zien hoe een punt tot oneigenlijk punt kan worden gemaakt.
Willen we de oneigenlijke rechte vinden, dan moet dat met twee punten (twee verschillende richtingen).

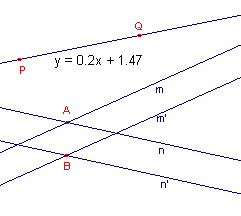
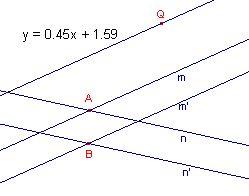
Allereerst laten we het punt P samenvallen met het oneigenlijk punt van m en m'. De lijn PQ (de lijn door Q is dan evenwijdig aan de lijn m). En vervolgens laten we Q samenvallen met het oneigenlijk punt van de lijnen n en n'.
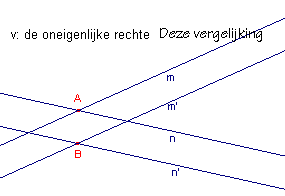
In de rechter figuur zien we dat Cabri de lijn PQ "herkent" als oneigenlijke rechte. Op de plaats van de vergelijking staat nu v: de oneigenlijke rechte (doordat de Wijzer er op gericht is, staat er ook: Deze vergelijking). De tekst "v:" geeft aan dat we te doen hebben met een "vergelijking".

Opmerking
De door Cabri gebruikte tekst (v: de oneigenlijke rechte) is afhankelijk van de gebruikte taalmodule van Cabri, in dit geval is dat nederlands_d.cgl.
Klik hier voor het downloaden van dit bestand [ca. 16Kb, ZIP-formaat].
[einde Opmerking]

Toepassing 10.1 
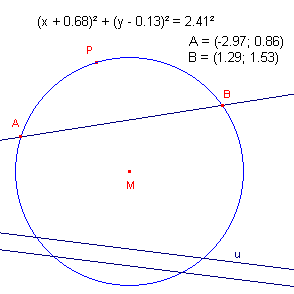
Zijn M en P twee punten en is C de cirkel met middelpunt M die gaat door P.
A en B zijn de snijpunten van een rechte lijn met de cirkel.
De co�rdinaten van A en B en de vergelijking van de cirkel zijn eveneens weergegeven.
De rechte lijn u (samen met u') bepaalt een oneigenlijk punt.
De onderstaande figuren laten nu zien wat er gebeurt als we het punt M laten samenvallen met het oneigelijk punt van de lijn u.

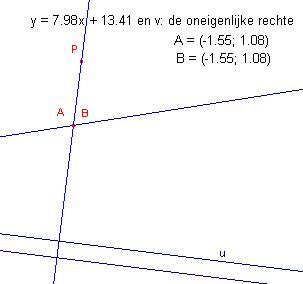			De cirkel "valt uiteen" in de oneigenlijke rechte en een lijn loodrecht op de richting van u. De snijpunten A en B vallen samen op de re�le rechte lijn.
			In de hiernaast staande figuren is te zien wat er gebeurt als het punt P samenvalt met het oneigenlijk punt van de lijn u. De punten A en B zijn dan oneigenlijke punten en de cirkel ontaardt in de (dubbel getelde) oneigenlijke rechte.

Toepassing 10.2 
We kunnen met Cabri nu eenvoudig laten zien, dat de poollijn van het middelpunt van een cirkel tov. die cirkel de oneigenlijke rechte is.
Klik hier voor deze illustratie.

Toepassing 10.3 
We kunnen ook illustreren, dat een parabool raakt aan de oneigenlijke rechte.
Klik hier voor deze illustratie.

Vorige

Begin

Volgende

[faq10.htm] laatst wwijziging op: 09-07-01